
- •Глава 2. Введение в анализ
- •§ 1. Некоторые свойства множества действительных чисел
- •§ 2. Предел последовательности
- •§ 3. Предел функции
- •§ 4. Бесконечно малые и их свойства
- •§ 5. Основные теоремы о пределах
- •§ 6. Замечательные пределы
- •§ 7. Непрерывность функции. Классификация точек разрыва
- •§ 8. Свойства непрерывных функций
- •§ 9. Сравнение функций. Асимптотические равенства
§ 9. Сравнение функций. Асимптотические равенства
Пусть
![]() и
и
![]() – бесконечно
малые функции в точке
– бесконечно
малые функции в точке
![]() .
.
Определение 1.
Если
![]()
![]() =
0,
то функцию
=
0,
то функцию
![]() называют бесконечно малой более высокого
порядка малости по сравнению с
называют бесконечно малой более высокого
порядка малости по сравнению с
![]() и пишут
и пишут
![]() =
o(
=
o(![]() )
при
)
при
![]()
![]() .
.
Пример 1.
Сравнить бесконечно малые
![]() =
=
![]() и
и
![]() =
sin
=
sin![]() в точке
в точке
![]() =
0.
=
0.
Решение.
Найдём
![]()
![]() =
=
![]()
![]() = 0
1 = 0. Поэтому
= 0
1 = 0. Поэтому
![]() = o(sin
= o(sin![]() )
при
)
при
![]()
0.
0.
Определение 2.
Если
![]()
![]() =
c
0, то
=
c
0, то
![]() и
и
![]() называют
бесконечно малыми одного порядка малости
и пишут
называют
бесконечно малыми одного порядка малости
и пишут
![]() =
O(
=
O(![]() )
при
)
при
![]()
![]() .
В частности, если
.
В частности, если
![]()
![]() =
c
0, то говорят,
что
=
c
0, то говорят,
что
![]() имеет k-й
порядок малости по сравнению с
имеет k-й
порядок малости по сравнению с
![]() при
при
![]()
![]() .
Действительное число k
называют
порядком малости, а сравнивают чаще
всего с функцией
.
Действительное число k
называют
порядком малости, а сравнивают чаще
всего с функцией
![]() =
=
![]() –
–
![]() .
Например, бесконечно малая в нуле функция
.
Например, бесконечно малая в нуле функция
![]() =
=
![]() имеет
четвертый порядок малости по сравнению
с
имеет
четвертый порядок малости по сравнению
с
![]() =
=
![]() .
Действительно,
.
Действительно,
![]()
![]() =
=
![]()
 =
3.
=
3.
Определение 3.
Если
![]()
![]() =
1,
=
1,
![]() и
и
![]() называются эквивалентными,
или асимптотически
равными
бесконечно
малыми в точке
называются эквивалентными,
или асимптотически
равными
бесконечно
малыми в точке
![]() .
Пишут
.
Пишут
![]() ~
~
![]() при
при
![]()
0. Например,
0. Например,
![]()
![]() = 1
sin
= 1
sin![]() ~
~
![]() при
при
![]()
0.
0.
Пример 2.
Доказать, что arcsin![]() ~
~
![]() при
при
![]()
0.
0.
Решение.
![]()
![]() =
=
 =
=
![]()
![]() = 1. Что и
требовалось доказать.
= 1. Что и
требовалось доказать.
Пример 3.
Доказать, что ln
(1 +
![]() )
~
)
~
![]() при
при
![]()
0.
0.
Решение.
![]()
![]() =
=
![]()
![]() =
=
![]() =
=
=![]()
![]() =
=![]() =
=![]() =
1
ln (1 +
=
1
ln (1 +
![]() )
~
)
~
![]() .
.
Заметим, что мы доказали третье равенство §6, приведённое в том параграфе без доказательства.
Можно доказать
следующие свойства эквивалентных
бесконечно малых в некоторой точке
![]() :
:
-
если
 ~
~
 ,
то
,
то
 ~
~
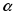 ;
; -
если
 ~
~
 ,
а
,
а
 ~
~
 ,
то
,
то
 ~
~
 ;
; -
если
 ~
~
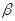 ,
то
,
то
 =
=
 + o(
+ o( );
); -
если
 =
=
 + o(
+ o( ),
то
),
то
 ~
~
 .
.
Определение 4.
Если
![]() =
=
![]() + o
+ o![]() ,
A
0,
,
A
0,
![]() > 0,
то выражение
> 0,
то выражение
![]() называется главной
степенной частью
бесконечно малой функции
называется главной
степенной частью
бесконечно малой функции
![]() в точке
в точке
![]() =
=
![]() .
.
Пример 4.
Выделить главную степенную часть
бесконечно малых функций
![]() =
=
![]() ,
,
![]() =
=
![]() в точке
в точке
![]() = 0.
= 0.
Решение. Очевидно,
![]() ~
~
![]() ~
~
![]() ,
,
![]() ~
~
![]() ~
~
![]() ,
поэтому
,
поэтому
![]() =
=
![]() +
o
(
+
o
(![]() ),
),
![]() =
=
![]() + o
(
+ o
(![]() ).
Главные степенные части:
).
Главные степенные части:
![]() и
и
![]() .
.
Теорема.
Если
![]() ~
~
![]() ,
,
![]() ~
~
![]() при
при
![]()
![]() и
и
![]()
![]() существует, то
существует, то
![]()
![]() =
=
![]()
![]() .
.
Доказательство.
![]()
![]() =
=
![]()
![]() =
=
![]()
![]()
![]()
![]()
![]()
![]() =
=
=
![]()
![]() .
Теорема
доказана.
.
Теорема
доказана.
Теоремой часто пользуются при нахождении пределов функции.
Пример 5.
Найти
![]()
![]() .
.
Решение. Воспользуемся теоремой и результатом примера 4.
![]()
![]() =
=
![]()
![]() = 2.
= 2.
Замечание. Аналогично сравниваются и бесконечно большие функции в некоторой точке.
