
- •Глава 1. Функции комплексного переменного
- •§1. Понятие функции комплексного переменного. Предел, непрерывность функции
- •§2. Производная функции комплексного переменного. Понятие аналитической функции
- •§3. Понятие ветви многозначной функции
- •§4. Геометрический смысл производной
- •§5. Примеры конформных отображений
- •§6. Интеграл от функции комплексного переменного
- •§7. Ряды Тейлора и Лорана
- •§8. Классификация особых точек. Вычеты
- •§9. Вычисление интегралов с помощью вычетов Из определения вычета следует
Глава 1. Функции комплексного переменного
§1. Понятие функции комплексного переменного. Предел, непрерывность функции
С
некоторыми функциями комплексного
переменного мы уже встречались (см. §2
гл.1, ч.1). Дадим теперь общее определение
функции комплексного переменного.
Рассмотрим множество E
комплексных чисел
![]() ,
лежащих в комплексной плоскости (z),
и множество G
комплексных чисел
,
лежащих в комплексной плоскости (z),
и множество G
комплексных чисел
![]() лежащих в комплексной плоскости (w)
(см. рис. 1).
лежащих в комплексной плоскости (w)
(см. рис. 1).

Определение
1. Если каждому
комплексному числу
![]() поставлено в соответствие одно или
несколько комплексных чисел множества
G,
то говорят, что на множестве
поставлено в соответствие одно или
несколько комплексных чисел множества
G,
то говорят, что на множестве
![]() задана однозначная или многозначная
функция комплексного переменного. Пишут
задана однозначная или многозначная
функция комплексного переменного. Пишут
![]()
Множество E называют областью определения функции, а множество G - множеством значений функции.
Согласно
определению 1 каждой паре действительных
чисел
![]() поставлена в соответствие пара
действительных чисел
поставлена в соответствие пара
действительных чисел
![]() Иными словами, на множестве E
заданы две
вещественные функции
Иными словами, на множестве E
заданы две
вещественные функции
![]() и
и
![]() двух вещественных переменных, т. е. одна
функция комплексного переменного
двух вещественных переменных, т. е. одна
функция комплексного переменного
![]() эквивалентна
двум вещественным функциям, при этом
эквивалентна
двум вещественным функциям, при этом
![]()
Приведем несколько примеров.
Пример 1.
![]()
![]() Эта
функция однозначная.
Эта
функция однозначная.
Пример 2.
![]()
Эта функция многозначная (n-значная).
Пример
3.
![]()
Эта функция бесконечнозначная.
Все
эти функции заданы на всей комплексной
плоскости, исключая бесконечно удаленную
точку
![]() Последняя функция не определена еще и
в точке
Последняя функция не определена еще и
в точке
![]() Заметим, что бесконечно удаленная точка
Заметим, что бесконечно удаленная точка
![]() на комплексной плоскости единственная.
на комплексной плоскости единственная.
Говорят,
что функция
![]() отображает множество E
в множество
G.
отображает множество E
в множество
G.

![]() Найдем область G,
в которую отобразит функция
Найдем область G,
в которую отобразит функция
![]() область E.
Пусть
область E.
Пусть
![]() тогда
тогда
![]() Отсюда ясно, что функция
Отсюда ясно, что функция
![]() отображает сектор E
в верхний полукруг радиуса
отображает сектор E
в верхний полукруг радиуса
![]() (см. рис. 2).
(см. рис. 2).
Это отображение взаимнооднозначное, т.е. каждой точке множества Е (прообразу) соответствует единственная точка (образ) множества G. И наоборот, образу соответствует единственный прообраз.
Заметим, что границе области E соответствует граница области G.
Возьмем
теперь в качестве области E
сектор
![]()
![]() При отображении
При отображении
![]() точки, лежащие на луче
точки, лежащие на луче
![]() отображаются в точки луча
отображаются в точки луча
![]() и точки, лежащие на луче
и точки, лежащие на луче
![]() отображаются в точки того же луча
отображаются в точки того же луча
![]()
![]() т.е. взаимная однозначность отображения
нарушается.
т.е. взаимная однозначность отображения
нарушается.
Чтобы
сохранить взаимную однозначность
отображения, сделаем разрез комплексной
плоскости
![]() по положительной полуоси u
и будем
считать, что верхний берег разреза –
это образ луча
по положительной полуоси u
и будем
считать, что верхний берег разреза –
это образ луча
![]() а нижний – образ луча
а нижний – образ луча
![]() (см. рис. 3).
(см. рис. 3).

Если
областью E
является сектор
![]()
![]() то взаимная однозначность отображения
то взаимная однозначность отображения
![]() опять нарушится. Чтобы ее сохранить,
предположим, что при изменении аргумента
прообраза от
опять нарушится. Чтобы ее сохранить,
предположим, что при изменении аргумента
прообраза от
![]() до
до
![]() образ соскальзывает с нижнего разреза
плоскости
образ соскальзывает с нижнего разреза
плоскости
![]() на второй (нижний) слой той же плоскости
на второй (нижний) слой той же плоскости
![]() (см. рис. 4).
(см. рис. 4).
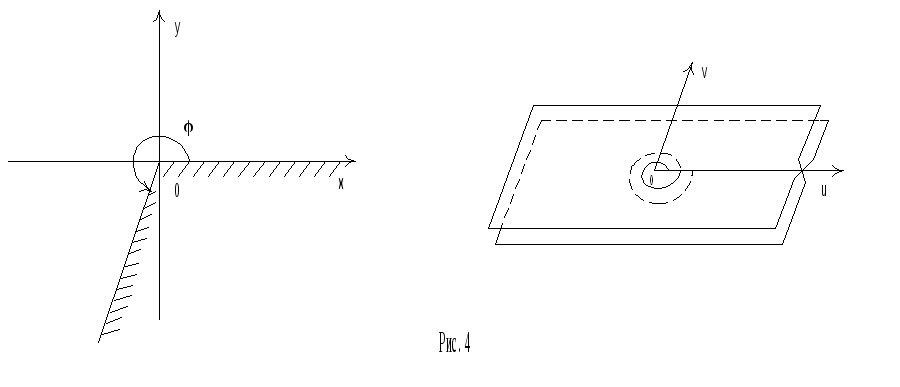
В
этом случае образы точек, лежащие на
лучах, например,
![]() и
и
![]() будут лежать на одном луче
будут лежать на одном луче
![]() но первые на верхнем листе плоскости
но первые на верхнем листе плоскости
![]() ,
а вторые на нижнем, и взаимная однозначность
отображения сохранится.
,
а вторые на нижнем, и взаимная однозначность
отображения сохранится.
Ясно
,что вся плоскость z
функцией
![]() отобразится в трехслойную плоскость
отобразится в трехслойную плоскость
![]() с разрезом по положительной полуоси u.
При этом верхний берег разреза первого
листа совпадает с нижним берегом разреза
третьего.
с разрезом по положительной полуоси u.
При этом верхний берег разреза первого
листа совпадает с нижним берегом разреза
третьего.
Если
![]()
![]() то образом плоскости z
будет n–слойная
(n-листная)
плоскость
то образом плоскости z
будет n–слойная
(n-листная)
плоскость
![]() с разрезом по действительной полуоси
u.
Такой многослойный образ называют
поверхностью
Римана.
с разрезом по действительной полуоси
u.
Такой многослойный образ называют
поверхностью
Римана.
Пусть
областью определения функции
![]() является полоса
является полоса
![]() Найдем образ линии
Найдем образ линии
![]() т.е. кривую, в которую она отображается
функцией
т.е. кривую, в которую она отображается
функцией
![]()
Запишем
уравнение прямой
![]() в комплексном виде:
в комплексном виде:
![]()
![]() параметр.
параметр.
Тогда
![]() (1)
(1)
Уравнения
(1) являются параметрическими уравнениями
образа линии
![]() Исключив параметр
t,
получим
Исключив параметр
t,
получим
![]() т.е. образом линии
т.е. образом линии
![]() является парабола.
является парабола.
При
![]() т.е. прямая
т.е. прямая
![]() отобразится в отрицательную полуось.
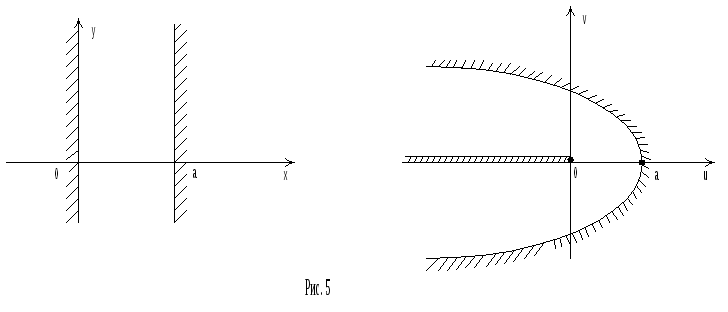
Полоса
отобразится в отрицательную полуось.
Полоса
![]() отобразится, очевидно, в часть плоскости
внутри параболы с разрезом по отрицательной
полуоси (см. рис. 5).
отобразится, очевидно, в часть плоскости
внутри параболы с разрезом по отрицательной
полуоси (см. рис. 5).
Рассмотрим последовательность комплексных чисел
![]() (2)
(2)
Определение
2. Число
![]() называется пределом последовательности
(2), если
называется пределом последовательности
(2), если
![]() при
при
![]() Пишут
Пишут
![]()
Если
![]() то из определения 2 следует
то из определения 2 следует
![]() при
при
![]() Следовательно,
Следовательно,
![]()
![]() при
при
![]() (3)
(3)
Очевидно
и обратное утверждение, если выполняется
(3), то
![]()
Если
![]()
![]()
![]()
![]() то
то
![]() при
при
![]() если
если
![]() (4)
(4)
Определение
3. Число
![]() называется пределом
однозначной
функции
называется пределом
однозначной
функции
![]() в точке
в точке
![]() если для всякой последовательности
аргумента
если для всякой последовательности
аргумента
![]() сходящейся к
сходящейся к
![]() соответствующая последовательность
значений функции
соответствующая последовательность
значений функции
![]() сходится
к
сходится
к
![]() Пишут
Пишут
![]()
Подчеркнем,
что если предел функции существует, то
он не зависит ни от способа, ни от пути
стремления последовательности
![]() к точке
к точке
![]()
Если![]()
![]()
![]()
то
из существования предела
![]() следует существование следующих
пределов:
следует существование следующих
пределов:
![]()
![]() (5)
(5)
![]()
![]()
![]() (6)
(6)
Если
![]() то функция называется непрерывной
в точке
то функция называется непрерывной
в точке
![]() Функция,
непрерывная в каждой точке некоторой
области, называется непрерывной в этой
области. Например, функция
Функция,
непрерывная в каждой точке некоторой
области, называется непрерывной в этой
области. Например, функция
![]() непрерывна во всей комплексной плоскости.
непрерывна во всей комплексной плоскости.
![]()
