6.2. Геометрический смысл двойного интеграла

Пусть требуется найти объем криволинейного цилиндра – тела, ограниченного сверху поверхностью , снизу некоторой замкнутой областью D, лежащей в плоскости Оxy, а по бокам образующими прямыми линиями, параллельными оси и проходящими через граничные точки области D (рис. 76). Разобьем область D на n элементарных областей с помощью произвольно выбранных прямых, параллельных осям Оx и Оy. Через эти прямые проведем плоскости, параллельные координатным плоскостям Оxz и Оyz. С помощью этих плоскостей криволинейный цилиндр будет разбит на n элементарных цилиндров с основаниями . В каждой области выберем произвольную точку и вычислим значение функции . Найдем приближенно объем каждого элементарного цилиндра

,

где  площадь элементарной области .

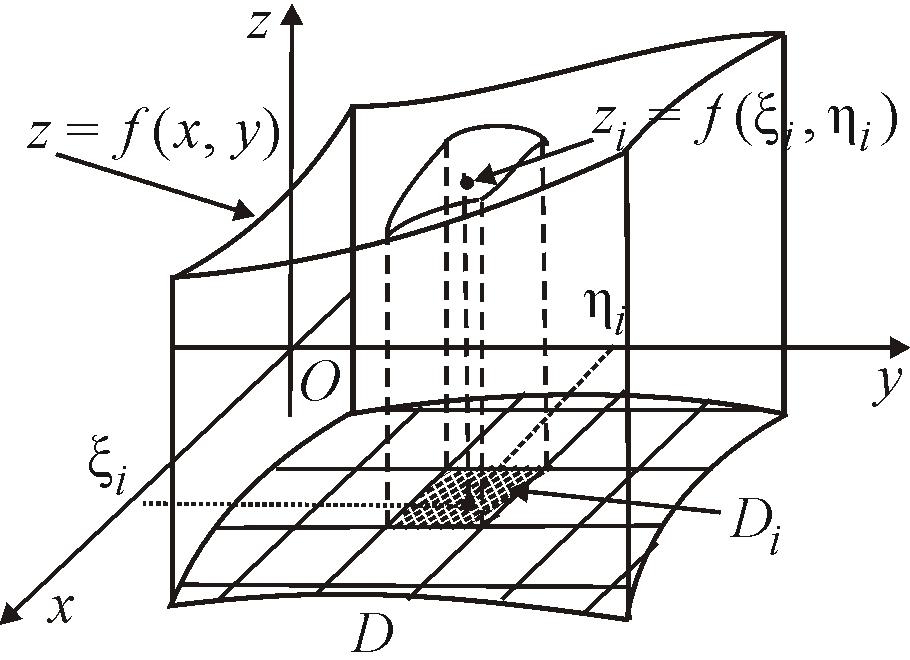
Рис. 76

Найдем приближенно объем всего криволинейного цилиндра

.

Для нахождения точного значения объема криволинейного цилиндра перейдем к пределу при неограниченном возрастании числа n элементарных областей и при стремлении к нулю наибольшей площади элементарных областей , т.е. . Найдем

.

6.3. Свойства двойных интегралов

1. .

2. .

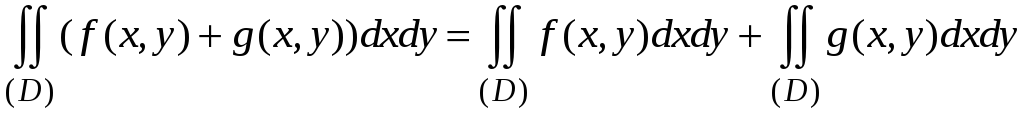3. Если область интегрирования D состоит из двух непересекающихся областей и (), то

.

4. Так как функция непрерывна в области D, то существует такая точка этой области, что

,

где S - площадь области D.

Это свойство называется теоремой о среднем.

6.4. Вычисление двойных интегралов

Пусть функция является непрерывной и ограниченной в области D. Область D ограничена прямыми , и кривыми , , (рис. 77).

Рис. 77

Данный интеграл найдем как объем криволинейного цилиндра.

Отрезок разобьем с помощью произвольно выбранных точек

на n элементарных отрезков длиной , i = 1, 2, …, n.

Через точки деления проведем плоскости параллельно плоскости Oyz. Эти плоскости разобьют криволинейный цилиндр на n элементарных криволинейных цилиндров. Найдем площадь каждого сечения

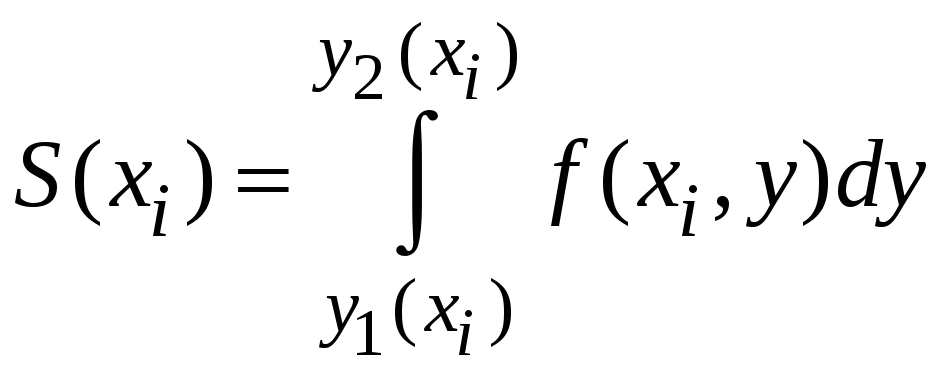, i = 1, 2, …, n.

Объем каждого элементарного цилиндра найдем приближенно как произведение основания на высоту . Получим..

Объем всего криволинейного цилиндра приближенно равен

.

Перейдем к пределу при и , получим точное значение объема криволинейного цилиндра

.

Таким образом, двойной интеграл рассматриваемого вида находится по формуле

.

Если область D ограничена прямыми , и кривыми , , , то аналогично можно получить формулу

.

Если область D ограничена прямыми , , , , то двойной интеграл по этой прямоугольной области находится по формуле

.

Пример 5.20. Найти , где (рис. 78).

Рис. 78

Находим .

Пример 5.21. Вычислить двойной интеграл по области

(рис. 79).

Рис. 79

Находим .

Пример 5.22. Вычислить двойной интеграл , где область D

ограничена линиями: (рис. 80). Затем изменить порядок интегрирования, и снова вычислить этот интеграл.

Рис. 80

Находим .

Изменим порядок интегрирования

.