
- •Глава 5. Определенный интеграл
- •5.1. Задачи, приводящие к понятию определенного интеграла
- •5.2. Интегральные суммы, их свойства
- •Определение определенного интеграла
- •5.3. Взаимосвязь определенного и неопределенного интегралов. Формула Ньютона - Лейбница
- •5.4. Свойства определенного интеграла
- •5.5. Методы интегрирования определенных интегралов
- •5.6. Несобственные интегралы с бесконечными пределами интегрирования
- •5.7. Теоремы о сходимости несобственных интегралов с бесконечными пределами интегрирования
- •5.8. Несобственные интегралы от разрывных функций, неограниченных в точках разрыва
- •5.9. Теоремы о сходимости несобственных интегралов от разрывных функций
- •5.10. Геометрические приложения определенных интегралов
- •5.10.1. Вычисление площадей фигур
- •5.10.2. Вычисление объемов тел вращения
- •5.10.3. Длина дуги кривой
- •5.11. Численные методы нахождения определенных интегралов
- •5.11.1. Формулы прямоугольников
- •5.11.2. Формула трапеций
- •5.11.3. Формула Симпсона для приближенного вычисления определенных интегралов
- •5.12. Производная интеграла, зависящего от параметра
- •Глава 6. Двойные интегралы
- •6.1. Определение двойного интеграла
- •6.2. Геометрический смысл двойного интеграла
- •6.3. Свойства двойных интегралов
- •6.4. Вычисление двойных интегралов
- •6.5. Двойные несобственные интегралы с бесконечными пределами интегрирования
5.5. Методы интегрирования определенных интегралов
При вычислении определенных интегралов используются те же методы, что и при нахождении неопределенных интегралов. Однако, имеются некоторые особенности.
1. Замена переменной
в определенном интеграле отличается
от замены переменной в неопределенном
интеграле тем, что в результате замены
изменяются пределы интегрирования и
нет необходимости выполнять обратную
замену. Пусть функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
функция
,
функция
![]() имеет непрерывную производную на
отрезке
имеет непрерывную производную на
отрезке
![]() .
Тогда
.
Тогда
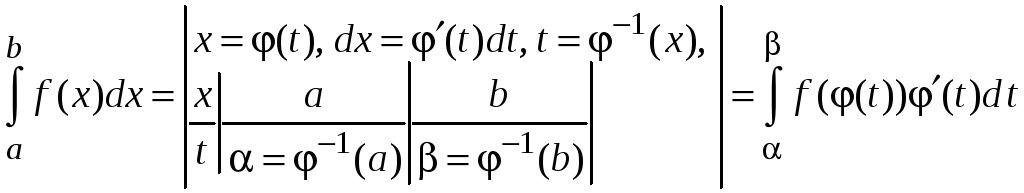 .
.
Пример 5.1.


 .
.
-
Интегрирование по частям.
Теорема 5.1. Если
функции
![]() и
и
![]() дифференцируемые и имеют непрерывные
производные на отрезке
дифференцируемые и имеют непрерывные
производные на отрезке
![]() ,
то
,
то
 .
.
Д о к а з а т е л ь с т в о.
Так как
![]() ,
то функция
,
то функция
![]() является первообразной для функции
является первообразной для функции
![]() и по формуле Ньютона-Лейбница
и по формуле Ньютона-Лейбница
 .
.
Отсюда, используя свойства определенного интеграла, получаем

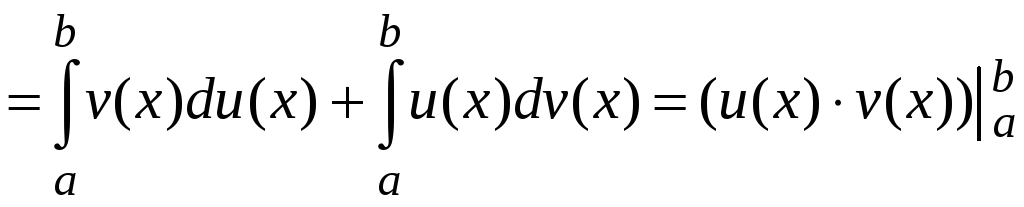
или
 .
.
Пример 5.2. Найти
 ,
где
,
где
![]() .
.
Используем
интегрирование по частям для нахождения
рекуррентной формулы для вычисления
интегралов вида
![]() при любом n
N.
при любом n
N.

 .
.
Учтем, что
![]() ,
получим
,
получим

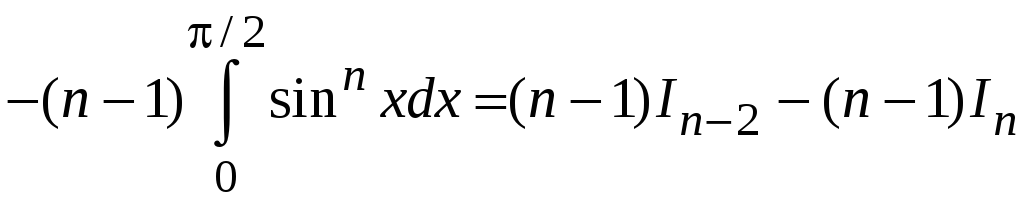 .
.
Получили уравнение
относительно интеграла
![]()
![]() .
.
Отсюда получаем рекуррентную формулу
![]()
![]() .
.
Используя данную
формулу, можно вычислить интеграл вида
![]() при любой степени n
подынтегральной функции. Рассмотрим
два случая, когда n
– четное и когда n
– нечетное.
при любой степени n
подынтегральной функции. Рассмотрим
два случая, когда n
– четное и когда n
– нечетное.
-
Если
 четное, то
четное, то
 .
.
Найдем
 ,
,
![]() .
.
Например,
 .
.
2. Если
![]() +1
нечетное, то
+1
нечетное, то
![]() .
.
Найдем
 ,
,
![]() .
.
Например,
 .
.
5.6. Несобственные интегралы с бесконечными пределами интегрирования
В рассмотренных
выше определенных интегралах вида
 предполагалось, что функция
предполагалось, что функция
![]() является непрерывной, пределы
интегрирования являются конечными
величинами. Однако, в прикладных задачах,
решаемых с помощью методов математического
анализа, часто приходится находить
интегралы с бесконечными пределами и
от разрывных функций. Такие интегралы
называются несобственными.
является непрерывной, пределы
интегрирования являются конечными
величинами. Однако, в прикладных задачах,
решаемых с помощью методов математического
анализа, часто приходится находить
интегралы с бесконечными пределами и
от разрывных функций. Такие интегралы
называются несобственными.
1. Несобственные интегралы с бесконечными пределами интегрирования определяются следующим образом.
 ,
,
 ,
,
 ,
где
,
где
![]() .
.
Если в несобственном интеграле пределы существуют (сходятся), то интеграл называется сходящимся, иначе – расходящимся.
Для данных несобственных интегралов справедливы обобщенные формулы Ньютона-Лейбница
 ;
;
 ;
;
 .
.
Геометрический
смысл несобственного интеграла состоит
в том, что он определяет площадь
криволинейной трапеции, неограниченной
на бесконечности. Для интеграла
 она имеет вид (рис.61).
она имеет вид (рис.61).

Пример 5.3. Найти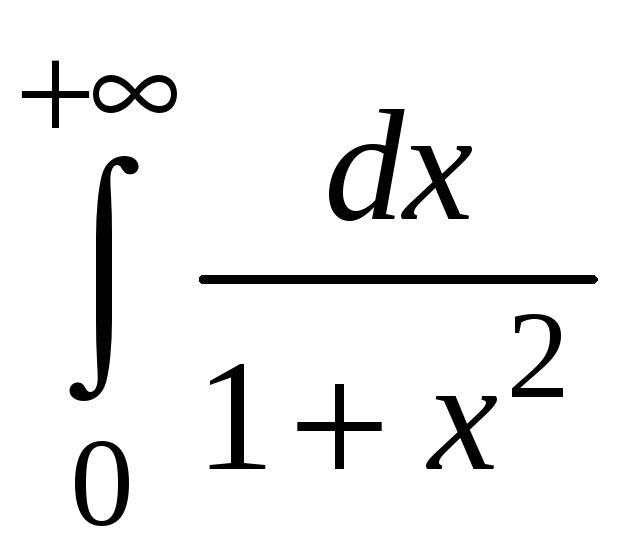 .
.
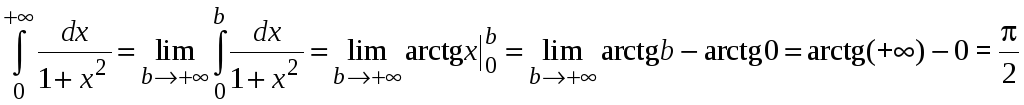 .
.
Пример 5.4.
Исследовать
на сходимость интеграл .
.
 .
.
Данный интеграл расходится, так как предел от sinx при х+ не существует.
Пример 5.5.
Исследовать
на сходимость интеграл
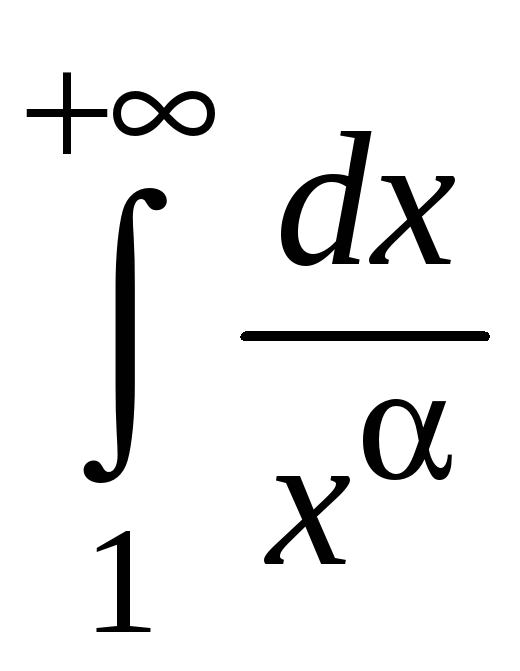 ,
где
,
где
![]() .
.
Если
![]() ,
то
,
то
 расходится.
расходится.
Если
![]() ,
то
,
то
 расходится
расходится
Если
![]() ,
то
,
то

сходится.
Таким образом,
данный интеграл сходится при
![]() и расходится при
и расходится при![]() .
.
Данный интеграл часто используется в других разделах высшей математики.
5.7. Теоремы о сходимости несобственных интегралов с бесконечными пределами интегрирования
В практических задачах часто достаточно определить только сходимость интеграла, а не его величину.
Теорема 5.2. Если
непрерывные функции
![]() и
и
![]() на промежутке
на промежутке
![]() удовлетворяют соотношению
удовлетворяют соотношению
![]() ,
то если
,
то если
 сходится, то и
сходится, то и
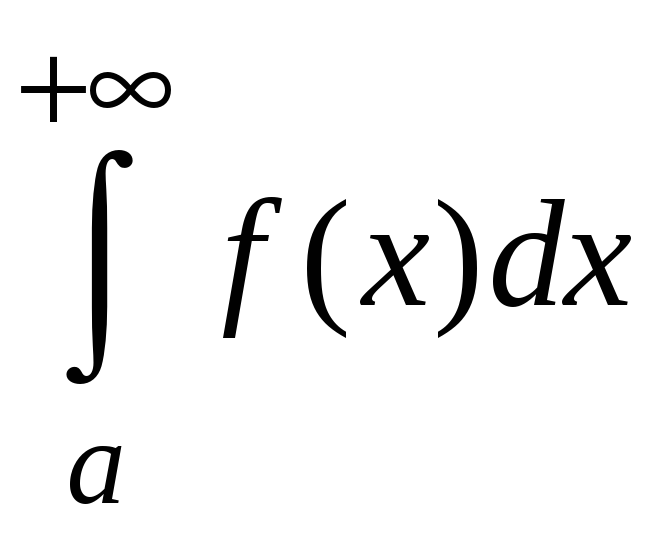 сходится; если же
сходится; если же
 расходится, то
расходится, то
 расходится.
расходится.
Д о к а з а т е л ь
с т в о. По свойству 5 определенных
интегралов, если
![]()
![]() ,
то
,
то
 .
Если
.
Если
 сходится, т. е. существует конечный
предел
сходится, т. е. существует конечный
предел
 ,
то интеграл
,
то интеграл
 ограничен. Ввиду того, что при возрастании
b
увеличивается интервал интегрирования
и подынтегральная функция
ограничен. Ввиду того, что при возрастании
b
увеличивается интервал интегрирования
и подынтегральная функция
![]()
![]() ,
то
,
то
 монотонно возрастает и, следовательно,
имеет предел
монотонно возрастает и, следовательно,
имеет предел
 .
.
Теперь обоснуем,
что если
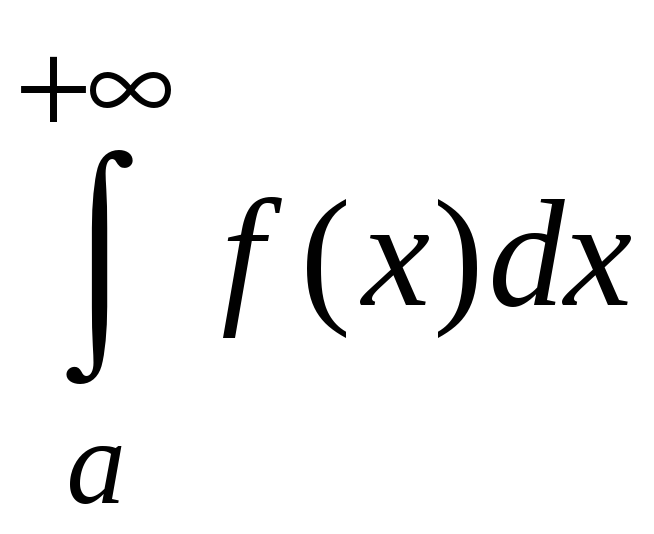 расходится, то
расходится, то
 расходится. От противного. Предположим,
что интеграл
расходится. От противного. Предположим,
что интеграл
 сходится. Тогда по первому утверждению
теоремы должен сходиться и интеграл
сходится. Тогда по первому утверждению
теоремы должен сходиться и интеграл .
В этом и состоит противоречие.
.
В этом и состоит противоречие.
Пример 5.6.
Исследовать
сходимость интеграла
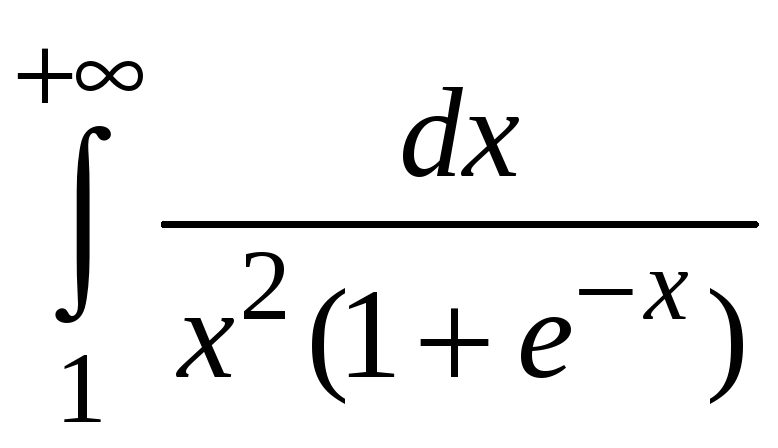 .
.
Для использования
теоремы 5.2 основная трудность состоит
в том, чтобы решить, какую функцию надо
подбирать
![]() или
или
![]() ,
т. е. что мы хотим доказать, сходится
интеграл или расходится. В данном
примере, очевидно,
,
т. е. что мы хотим доказать, сходится
интеграл или расходится. В данном
примере, очевидно,
 .
.
![]() сходится, так как степень
сходится, так как степень
![]() (см. пример 5.5). Следовательно, исходный
интеграл сходится.
(см. пример 5.5). Следовательно, исходный
интеграл сходится.
Пример 5.7.
Исследовать
сходимость интеграла
 .
.
Подбираем функцию
![]() ,
,

![]() .
.
Интеграл
 расходится, так как
расходится, так как
![]() (см. пример 5.5). Следовательно, исходный
интеграл расходится.
(см. пример 5.5). Следовательно, исходный
интеграл расходится.
Теорема 5.3. Если
функция
![]() непрерывна на промежутке
непрерывна на промежутке
![]() и
и
 сходится, то также сходится
сходится, то также сходится
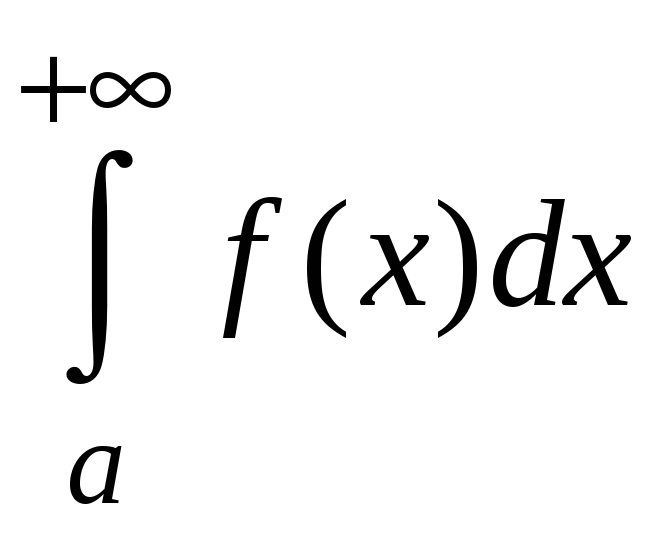 .
.
Если сходятся
одновременно интегралы
 и
и
 ,
то интеграл
,
то интеграл
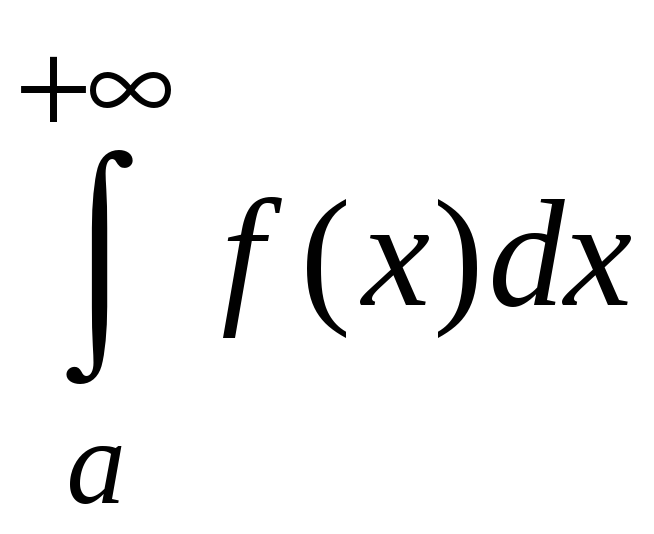 называется абсолютно сходящимся.
называется абсолютно сходящимся.
Д о к а з а т е л ь
с т в о. Для любого значения х
из промежутка
![]() справедливо неравенство
справедливо неравенство
![]() .
На основании свойства 5 для определенных
интегралов
.
На основании свойства 5 для определенных
интегралов
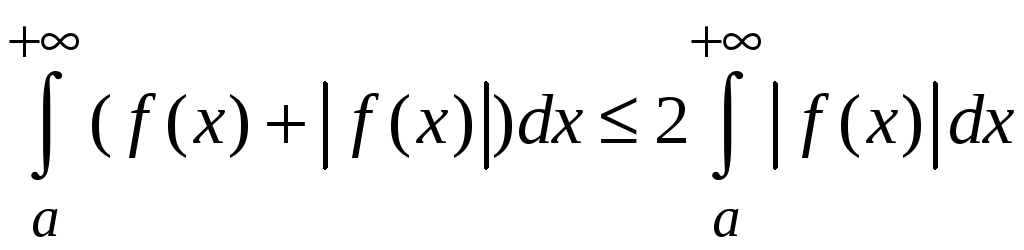 .
Так как по условию теоремы интеграл от
функции
.
Так как по условию теоремы интеграл от
функции
![]() сходится, то также сходится (по теореме
5.2)
сходится, то также сходится (по теореме
5.2)
 .
Следовательно, сходится разность
интегралов
.
Следовательно, сходится разность
интегралов
 .
.
Пример 5.8.
Исследовать
сходимость интеграла
 .
.
Для любых значений
х,
принадлежащих
промежутку
![]() ,
справедливы неравенства
,
справедливы неравенства
![]() и
и
 .
.
![]() сходится, так как степень
сходится, так как степень
![]() (см. пример 5.5). На основании теоремы 5.2
интеграл
(см. пример 5.5). На основании теоремы 5.2
интеграл
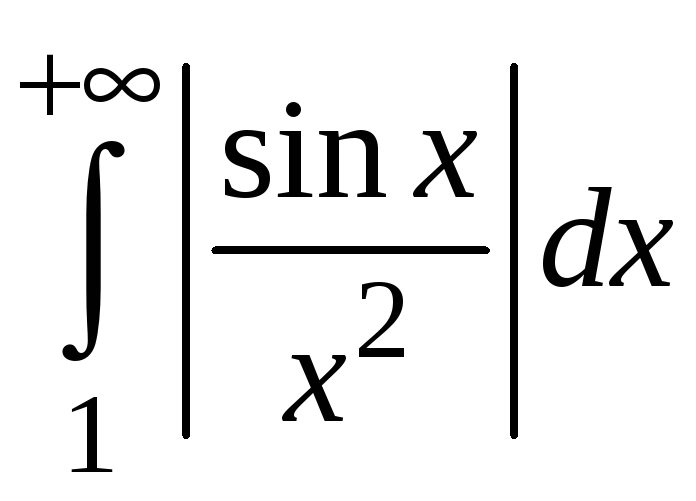 сходится. На основании теоремы 5.3 интеграл
сходится. На основании теоремы 5.3 интеграл
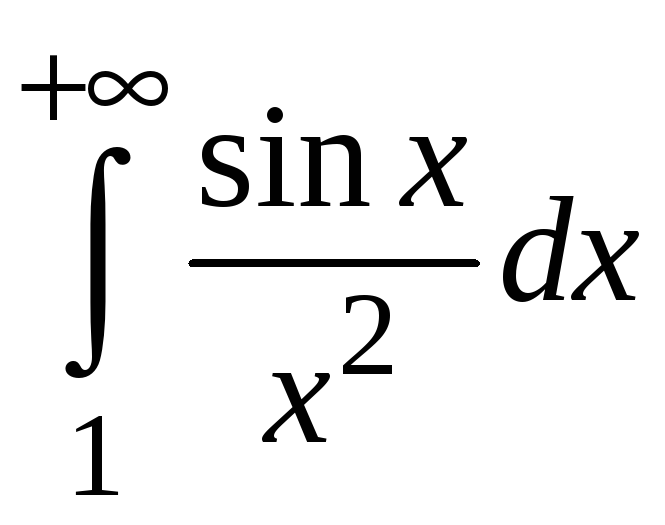 сходится абсолютно.
сходится абсолютно.
Теорема 5.4. Если
на промежутке
![]() для непрерывных неотрицательных функции
для непрерывных неотрицательных функции
![]() и
и
![]() (
(![]() ),
существует конечный предел отношения
функций
),
существует конечный предел отношения
функций
 ,
неравный нулю, то оба интеграла от этих
функций
,
неравный нулю, то оба интеграла от этих
функций
 и
и либо сходятся, либо расходятся
одновременно.
либо сходятся, либо расходятся
одновременно.
Д о к а з а т е л ь
с т в о. Пусть
 ,
,
![]() ,
,
![]() .
По определению предела
.
По определению предела
 .
.
Здесь сколь угодно малое положительное число.
Справедливы соотношения
 .
.
Так как
![]() ,
,
![]() ,
а
сколь угодно малое число, то
,
а
сколь угодно малое число, то
![]() и справедливо
и справедливо
![]() .
.
Используем это
неравенство и теорему 5.2. Если интеграл
 сходится, то интеграл
сходится, то интеграл
 также сходится. И наоборот, если интеграл
также сходится. И наоборот, если интеграл
 расходится, то и интеграл
расходится, то и интеграл
 расходится.
расходится.
Пример 5.9.
Исследовать
на сходимость интеграл
 .
.
Подынтегральную
функцию
 сравним с функцией
сравним с функцией
 .
Находим предел отношения функций
.
Находим предел отношения функций
 .
.
Предел является
конечной величиной, поэтому интегралы
от этих функций сходятся или расходятся
одновременно. Интеграл сходится, так как степень х
в подынтегральной
функции
сходится, так как степень х
в подынтегральной
функции
![]() (см. пример 5.5). Следовательно, исходный
интеграл также сходится.
(см. пример 5.5). Следовательно, исходный
интеграл также сходится.
Пример 5.10.
Исследовать
на сходимость интеграл
 .
.
Найдем предел
отношения функций
 и
и
![]() .
.
 .
.
Предел является конечной величиной, поэтому интегралы от этих функций сходятся или расходятся одновременно.
Интеграл
 расходится.
расходится.
Следовательно, исходный интеграл также расходится.
