1. Лабораторная работа №10

Применение кластерного анализа для классификации экономических объектов

Цель данной лабораторной работы заключается в изучении методов кластерного анализа и применение их для классификации экономических объектов.

1 Краткая теоретическая часть

1.1 Основные понятия, определения, формулы

При наличии нескольких признаков (исходных или обобщенных), задача классификации может быть решена методами кластерного анализа, которые отличаются от других методов многомерной классификации отсутствием обучающих выборок, т.е. априорной информации о распределении генеральной совокупности.

Пусть исследуется совокупность n объектов, каждый из которых характеризуется по k замеренным на нем признакам Х. Требуется разбить эту совокупность на однородные, в некотором смысле, группы (классы).

Полученные в результате разбиения группы обычно называются кластерами (claster – группа элементов, характеризуемых каким – либо общим свойством), таксонами (taxon - систематизированная группа любой категории), образами. Методы их нахождения - кластер- анализом.

Обычной формой представления исходных данных в задачах кластерного анализа служит матрица:

(1.1.1)

каждая строка которой, представляет результат измерений k, рассматриваемых признаков на одном из обследованных объектов. В конкретных ситуациях, может представлять интерес как группировка объектов, так и группировка признаков. В тех случаях, когда разница между двумя этими задачами не существенна, например, при описании некоторых алгоритмов, будем пользоваться только термином «объект», включая в это понятие и признак.

Матрица Х не является единственным способом представления данных в задачах кластерного анализа. Иногда, исходная информация задана в виде квадратной матрицы:

(1.1.2)

элемент r_ij , который определяет степень близости i-ого объекта к j-му. Большинство алгоритмов кластерного анализа полностью исходит из матрицы расстояний (или близостей), либо требует вычисления отдельных ее элементов, поэтому, если данные представлены в форме Х, то первым этапом решения задачи поиска кластеров будет выбор способа вычисления расстояний, или близости, между объектами и признаками.

Расстояние между объектами (кластерами) и мера близости

Наиболее трудным и наименее формализованным в задаче классификации является определение понятия однородности объектов.

В общем случае, понятие однородности объектов задается либо введением правила вычисления расстояний между любой парой исследуемых объектов либо заданием некоторой функции характеризующий степень близости i-ого и j-ого объектов. Если задана функция то близкие с точки зрения этой мерки объекты считаются однородными, принадлежащими к одному классу. Очевидно, что необходимо при этом сопоставлять с некоторыми пороговыми значениями, определяемыми в каждом случае по-своему.

Аналогично используется и мера близости , при задании которой нужно помнить о необходимости выполнения следующих условий: симметрии максимального сходства объекта с самим собой при , и монотонного убывания по мере увеличения т.е. из должно следовать неравенство

Выбор метрики или меры близости является узловым моментом исследования, от которого в основном зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом, конкретном случае, этот выбор должен производится по-своему, в зависимости от целей исследования, физической и статистической природы вектора наблюдений Х, априорных сведений о характере вероятностного распределения Х.

Рассмотрим наиболее широко используемые в задачах кластерного анализа расстояния и меры близости.

Обычное Евклидово расстояние

(1.1.3)

где - величина е –ой компоненты у i-ого (j-ого) объекта (е=1,2, …,k, i,j=1,2,…,n)

Использование этого расстояния оправдано в следующих случаях:

а) наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение с ковариационной матрицей вида т.е. Х взаимно независимы и имеют одну и ту же дисперсию, где - единичная матрица;

б) компоненты вектора наблюдений Х однородны по физическому смыслу и одинаково важны для классификации;

в) признаковое пространство совпадает с геометрическим пространством.

“Взвешенное” Евклидово пространство

(1.1.4)

применяется в тех случаях, когда каждой компоненте вектора наблюдений Х , удается переписать некоторый “вес” , пропорционально степени важности признака в задаче классификации. Обычно, принимают , где е=1,2,…,k.

Определение “весов”, как правило, связано с дополнительными исследованиями, например, организацией опроса экспертов и обработкой их мнений. Определение весов , только по данным выборки, может привести к ложным выводам.

Хеммингово расстояние

Используется как мера различия объектов, задаваемых дихотомическими признаками. Это расстояние определяется по формуле:

(1.1.5)

и равно числу несовпадений значений соответствующих признаков, в рассматриваемых i-м и j-м объектах.

Расстояние между группами

В ряде процедур классификации (кластер – процедур) используют понятие расстояние между группами объектов и меры близости двух групп объектов.

Пусть, - i-ая группа (класс, кластер), состоящая из объектов;

- среднее арифметическое векторных наблюдений группы, т.е. “центр тяжести” i-ой группы;

- расстояние между группами и .

Наиболее употребляемыми расстояниями и мерами близости между классами объектов являются:

• расстояние, измеряемое по принципу “ближайшего соседа” –

(1.1.6)

- расстояние, измеряемого по принципу “дальнего соседа” –

- расстояние, измеряемое по “центрам тяжести” групп -

(1.1.7)

(1.1.8)

• расстояние, измеряемое по принципу “средней связи” определяется как среднее арифметическое всех по парных расстояний между представителями рассматриваемых групп –

(1.1.9)

Академиком Колмогоровым было предложено “обобщенное расстояние” между классами, которое включает в себя, в качестве частных случаев, все рассмотренные выше виды расстояний.

Расстояние между группой элементов особенно важно, в так называемых, алгомеративных иерархичскеских кластер – процедурах, так как принцип работы таких алгоритмов состоит в последовательном объединении элементов, а затем и целых групп, сначала самых близких, а затем все более и более отдаленных друг от друга.

При этом рассмотрении между классами и , являющиеся объединением двух других классов и , можно определить по формуле:

(1.1.10)

где, и - расстояние между классами и

- числовые коэффициенты, значения которых определяют специфику процедуры, ее алгоритм.

Например, при и приходим к расстоянию, построенному по принципу “ближайшего соседа”. При и расстояние между классами определяется по принципу “дальнего соседа”, то есть как расстояние между двумя самыми дальними элементами этих классов.

И, наконец, при:

, (1.1.11)

соотношение приводит к расстоянию между классами, вычесленному как среднее из расстояний между всеми парами элементов, один из которых берется из одного класса, а другой из другого.

Функционалы качества разбиения

Под наилучшем разбиением, мы понимаем такое разбиение, при котором достигается экстремум выбранного функционала качества. Следует отметить, что выбор того или иного функционала качества, как правило, опирается на имперические соображения.

Существуют следующие характеристики функционала качества

• сумма внутриклассовых дисперсий

(1.1.12)

• сумма попарных внутриклассовых расстояний между элементами

(1.1.13)

Q₁(S) и Q₂(S) широко используются в задачах кластерного анализа для сравнения качества процедур разбиения;

• обобщенная внутриклассовая дисперсия

(1.1.14)

где det A - определитель матрицы А;

W_i - выборочная ковариационная матрица класса Si, элементы которой определяются по формуле

(1.1.15)

где х_iq - q-я компонента многомерного наблюдения х_i;

х_q - среднее значение q-ой компоненты, вычисленное по наблюдениям i-го класса.

1.2 Экспериментальная часть

В качестве примера рассмотрим задачу:

Организация занимающаяся продажей товаров решила расширить свой ассортимент для чего была получена опытная партия из 4 видов: Товар№1, Товар№2, Товар№3, Товар№4. Было также известно, что на данном рынке Товар№5 пользуется большим спросом, а Товар№6 продаётся плохо. На основе данных о продажах товаров за 12 месяцев (см. таблицу №1) определить какие товары из опытной партии пользовались высоким спросом. Принять, что товары имеют одинаковую цену.

Таблица №1

	Товар№1	Товар№2	Товар№3	Товар№4	Товар№5	Товар№6
Январь	658	746	458	394	753	418
Февраль	419	632	550	468	743	357
Март	742	601	424	328	732	290
Апрель	852	696	466	380	838	287
Май	799	634	423	379	819	203
Июнь	801	640	504	461	815	451
Июль	802	623	428	303	767	417
Август	789	683	573	458	769	394
Сентябрь	686	720	518	470	663	488
Октябрь	714	691	429	344	757	271
Ноябрь	668	671	577	384	815	260
Декабрь	733	696	508	309	719	458

Для решения данной задачи воспользуемся электронным документом klaster.mcd (которому для работы необходим klasterH.mcd) составленным в математическом процессоре Mathcad 7.

Приняв, что расстояния будут рассчитываться по методу ближайшего соседа все весовые коэффициенты равны 1 (“взвешенное” Евклидово пространство), получим матрицу расстояний и матрицу кластеров

Так как значение в 4 строке и во 6 столбце минимальное, то есть растояние между кластером 4 и 6 минимально, то они объединяются в один кластер.

Получаем на втором шаге

На третьем шаге

Н а четвёртом шаге

Н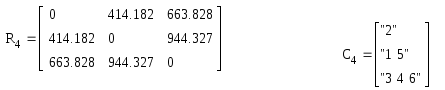 а пятом шаге

З аметим что с каждым шагом расстояние между объединяющимися кластерами увеличивается. Это будет хорошо видно если построить дентограмму

Рис. 1 Дентограмма

Как видно, Товар№4, Товар№3 обладают общим свойством с Товаром№6, то есть обладают низким спросом. Товар№2, Товар№1 обладают общим свойством с Товаром№5, то есть обладают высоким спросом. Следовательно фирме следует купить на следующий период товары №1, №2 и №5.

1.3 Задание на лабораторную работу

1. На основе исходных данных рассчитать матрицу расстояний и матрицу кластеров. X1, X2, X3, X4 – взять из лабораторной работы «Множественный регрессионный анализ». X5 = U4*U4*10.

2. Провести классификацию объектов. При этом расстояние рассчитывать по методу ближайшего соседа. Рассчитывать функционал качества Q2(S) для каждого шага.

3. Провести классификацию объектов. При этом расстояние рассчитывать по методу дальнего соседа. Рассчитывать функционал качества Q2(S) для каждого шага. Результаты сравнить с результатами задания 3.

При выполнении данной лабораторной работы рекомендуется использовать программу Mathcad.