Лабораторная работа № 7 Применение компонентного анализа при изучении социально-экономических явлений

1. Цель работы

Цель данной лабораторной работы заключается в освоении метода линейных компонент.

2. Краткая теоретическая часть

Основные понятия, определения, формулы

Во многих задачах обработки многомерных наблюдений и, в частности, в задачах классификации исследователя интересуют в первую очередь лишь те признаки, которые обслуживают наибольшую изменчивость (наибольший разброс) при переходе от одного объекта к другому.

С другой стороны, не обязательно для описания состояния объекта использовать какие-то из исходных, непосредственно замеренных на нем признаков. Так, например, для определения специфики фигуры че­ловека при покупке одежды достаточно назвать значения двух признаков (размер-рост), являющихся производными от измерений ряда параметров фигуры. При этом, конечно, теряется какая-то доля информации (портной измеряет до одиннадцати параметров на клиенте), как бы огрубляются (при агрегировании) получающиеся при этом классы. Однако, как пока­зали исследования, к вполне удовлетворительной классификации людей с точки зрения специфики их фигуры приводит система, использующая три признака, каждый из которых является некоторой комбинацией от боль­шого числа непосредственно замеряемых на объекте параметров.

Именно эти принципиальные установки заложены в сущность компонентного анализа. Компонентный анализ относится к многомерным методам снижения размерности. Он содержит один метод - метод главных компонент. В этом методе линейные комбинации случайных величин определяются характе­ристическими векторами ковариационной матрицы. Главные компонен­ты представляют собой ортогональную систему координат, в которой дис­персии компонент характеризуют их статистические свойства.

Компонентный анализ предназначен для преобразования системы исходных признаков, в систему новых показателей (главных компонент). Главные компоненты не коррелированны между собой и упорядочены по величине их дисперсий, причем, первая главная компонента, имеет наибольшую дисперсию, а последняя, k – ая, наименьшую. При этом выявляются неявные, непосредственно не измеряемые, но объективно существующие закономерности, обусловленные действием как внутренних, так и внешних причин.

Модель компонентного анализа имеет вид:

(1.2.1)

где - “вес”, факторная нагрузка, - ой главной компоненты на j-ой переменной; - значение v – ой главной компоненты для i-ого наблюдения (объекта), где v=1,2,…,k.

В

(1.2.2)

матричной форме модель (1.2.2) имеет вид:

где:

- матрица значений главных компонент размерности ;

- матрица факторных нагрузок размерности;

- транспонированная матрица A;

- значение v – ой главной компоненты у i – ого наблюдения (объекта);

- значение факторной нагрузки v - ой главной компоненты на j-й переменной.

Матрица F описывает n наблюдений в пространстве k главных компонент. При этом элементы матрицы F нормированы, то есть:

(1.2.3)

(1.2.4)

а главные компоненты не коррелированны между собой. Из этого следует, что,

(1.2.5)

где,

- единичная матрица размерности .

Выражение (1.2.11) может быть также представлено в виде:

(1.2.6)

при и 0 при

С целью интерпретации элементов матрицы A, рассмотрим выражение для парного коэффициента корреляции, между - переменной и, например, -ой главной компонентой. Будем иметь

П

(1.2.7)

ринимая во внимание, окончательно получим:

Рассуждая аналогично, можно записать в общем виде:

(1.2.8)

для всех и .

Таким образом, элемент матрицы факторных нагрузок А, характеризует тесноту линейной связи между - исходной переменной и - й главной компонентой, то есть .

Рассмотрим теперь выражение для дисперсии - й нормированной переменной. С учетом будем иметь:

где .

Окончательно получим:

(1.2.9)

По условию переменные нормированы и Таким образом, дисперсия -й переменной представлена своими составляющими, определяющими долю вклада в нее всех k главных компонент.

Полный вклад v-й главной компоненты в дисперсию всех k исходных признаков вычисляется по формуле:

(1.2.10)

Компонентный анализ проводится в следующей последовательности.

Н

(1.2.11)

а основании матрицы исходных данных:

р

(1.2.12)

азмерности , где - значение -ого показателя у -ого наблюдения (i=1,2,…,n; j=1,2,…,k) вычисляют средние значения показателей , а также и матрицу нормированных значений:

с

(1.2.13)

элементами:

Рассчитывается матрица парных коэффициентов корреляции:

(1.2.14)

с элементами:

(1.2.15)

где,

Н

(1.2.16)

а главной диагонали матрицы R т.е. при j=1,

Перейдем теперь непосредственно к отысканию собственных значений и собственных векторов корреляционной матрицы R.

Из линейной алгебры известно, что для любой симметрической матрицы R всегда существует такая ортогональная матрица U, что выполняется условие:

(1.2.17)

где,

- диагональная матрица собственных значений размерности ;

- ортогональная матрица собственных векторов размерности .

Так как матрица R положительно определена, т.е. ее главные миноры положительны, то все собственные значения положительны для всех v=1,2,…,k.

В компонентном анализе элементы матрицы - ранжированы Как будет показано ниже, собственное значение характеризует вклад v – й главной компоненты в суммарную дисперсию исходного признакового пространства.

Таким образом, первая главная компонента вносит наибольший вклад в суммарную дисперсию, а последняя k-ая – наименьший.

В ортогональной матрице U собственных векторов, v-й столбец является собственным вектором, соответствующим - му значению.

Собственные значения находятся как корни характеристического уравнения:

(1.2.18)

С

(1.2.19)

обственный вектор соответствующий собственному значению корреляционной матрицы R, определяется как отличное от нуля решение уравнения:

Н

(1.2.20)

ормированный собственный вектор равен:

Представим матрицу факторных нагрузок A в виде:

(1.2.21)

а

(1.2.22)

v-й столбец матрицы A:

г де, - собственный вектор матрицы R , соответствующий собственному значению :

Найдем норму вектора :

(1.2.23)

З

(1.2.24)

десь учитывалось, что вектор нормированный и Таким образом,

М

(1.2.25)

ожно сделать вывод, что собственное значение характеризует вклад v- й главной компоненты в суммарную дисперсию всех исходных признаков. Следует:

О

(1.2.26)

бщий вклад всех главных компонент в суммарную дисперсию равен k . Тогда удельный вклад v-й главной компоненты определяется по формуле:

(1.2.27)

Суммарный вклад m первых главных компонент определяется из выражения:

Обычно для анализа используют m главных компонент, суммарный вклад которых превышает 60-70%.

Матрица факторных нагрузок A используется для экономической интерпретации главных компонент, которые представляют линейные функции исходных данных. Для экономической интерпретации используется лишь те , для которых, .

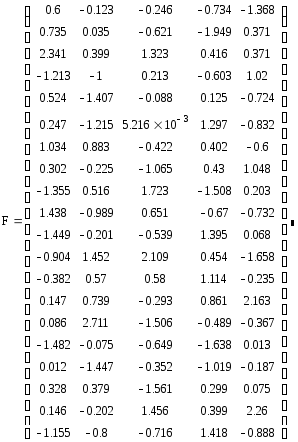
Значения главных компонент для каждого i-ого объекта задаются матрицей F .

М

(1.2.28)

атрицу значений главных компонент можно получить из формулы:

о

(1.2.29)

ткуда,

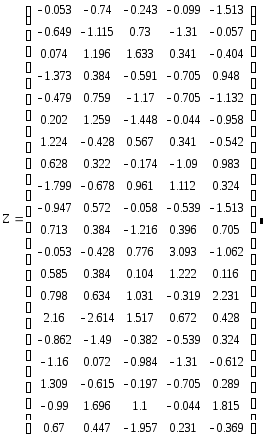
г де, Z-матрица нормированных значений исходных показателей.

3. Экспериментальная часть

В качестве примера рассмотрим объёмы производства (тыс. ед.) 5 видов тортов некоторой кондитерской фабрикой за последние 20 лет.

Таблица 1. Исходные данные

Вид №1	Вид №2	Вид №3	Вид №4	Вид №5
243	291	505	486	444
229	285	547	464	486
246	322	586	494	476
212	309	490	475	515
233	315	465	475	455
249	323	453	487	460
273	296	540	494	472
259	308	508	468	516
202	292	557	508	497
222	312	513	478	444
261	309	463	495	508
243	296	549	544	457
258	309	520	510	491
263	313	560	482	552
295	261	581	500	500
224	279	499	478	497
217	304	473	464	470
275	293	507	475	496
221	330	563	487	540
260	310	431	492	477

Проведём анализ полученных данных с помощью метода главных компонент.

М атематические ожидания значений показателей

С тандартные ошибки

М

(1.3.1)

атрица нормированных значений будет определяться по формуле

М

(1.3.2)

атрица парных коэффициентов корреляции R

М атрица собственных чисел R

М

(1.3.3)

атрица факторных нагрузок (весовых коэффициентов) ,

г де V – матрица собственных векторов R.

Главные компоненты

Т

(1.3.4)

.е. нормированные значения исходных признаков можно выразить через главные компоненты как

о

(1.3.5)

ткуда

И

(1.3.6)

з матрицы собственных чисел видно, что наибольший вклад в дисперсию исходных признаков вносят 2-я, 5-я, и 3-я компоненты (их суммарный вклад составляет 75.6%). Поэтому дальнейший анализ можно проводить, используя только эти 3 параметра. Остальные компоненты, вносящие наименьший вклад в дисперсию будем считать равными нулю. Т. е. мы предполагаем, что

Полученные значения главных компонент не имеют экономического смысла, но геометрически их можно трактовать как координаты 20 точек в пространстве R⁵ в системе координат, полученной поворотом на некоторый угол относительно другой системы, в которой по нормированным значениям и были построены эти точки.

Так как главные компоненты не коррелированы друг с другом, то их значения можно использовать в регрессионном анализе. Допустим, мы хотим исследовать зависимость некоторого признака Y (например, прибыли предприятия) от объёмов производства тортов. Поскольку объёмы производства каждого вида взаимосвязаны, то регрессионный анализ, проведённый по исходным данным, может привести к неадекватным результатам. Поэтому, лучше построить модель признака Y по главным компонентам (не обязательно по всем, в нашем случае можно взять только компоненты 1, 3, 4 и 5). Полученное соотношение Y=F(f) можно преобразовать в соотношение Y=F₁(z), а затем в Y=F₂(x). Полученная таким способом модель будет более точно описывать зависимость признаков, поскольку при её построении будут использованы некоррелированные друг с другом данные.

В нашем случае в качестве параметра Y возьмём объём спроса на торты в данном регионе за последние 20 лет.

Таблица №2. Спрос на торты за последние 20 лет

Объём спроса на торты (тыс. шт)
119.2
120.1
121.5
120.2
119.6
120.0
119.9
120.6
119.9
120.0
119.8
119.5
120.4
122.0
118.8
118.4
119.3
119.5
122.8
119.0

П

(1.3.7)

олученная модель примет вид

Ч

(1.3.8)

ерез переменные z модель запишется как

А

(1.3.9)

через исходные признаки x

Как видно из полученной модели наибольший вклад в спрос вносит вид №2, т. е. торты вида №2 за исследуемый период пользовались наибольшим спросом, торты №1 – наоборот не пользовались спросом. Большое значение свободного члена выражения показывает, что большая часть спроса на торты удовлетворялась тортами других видов, не рассмотренных здесь, т. е. тортами, выпускаемыми другими фабриками.