1. Магнитное взаимодействие проводников с токами. Контур с током в магнитном поле.

Расчет силы Ампера, действующей на единицу длины двух параллельных проводников с токами I₁ и I₂ (рис.2.9) дает величину:

, (2.14)

где d - расстояние между проводниками.

Данное выражение в системе единиц СИ служит основанием для введения единицы силы тока - ампер ( А ).

Проводники с одинаково направленными токами I₁ и I₂ взаимно притягиваются, а проводники с противоположно направленными токами отталкиваются друг от друга.

Замкнутый проводящий контур с током произвольной геометри­ческой формы, помещённый в однородное магнитное поле, испытывает действие вращающего момента сил М (рис.2.10),

, М = р _m Вsin , (2.15)

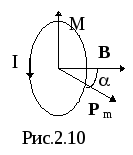
где: р _m - магнитный момент контура с током, а  - угол между магнитным моментом и магнитной индукцией.

М

омент сил стремится установить магнитный момент по направлению магнитной индукции B в положение устойчивого равновесия. Если внешние силы увеличивают угол , то они совершают работу против сил магнитного поля и тем самым увеличивают энергию контура, которую можно вычислить следующим способом:

, . (2.16)

Выражение, определяющее момент сил, действующий на контур с током в магнитном поле, дает еще один способ определения магнитной индукции:

Вектор магнитной индукции B численно равен отношению вра­щающего момента, действующего в магнитном поле на небольшую рамку с током, к магнитному моменту рамки при такой её ориентации в поле, когда это отношение достигает максимального значения; по направлению вектор B совпадает с вектором магнитного момента рамки, находящейся в положении устойчивого равновесия в рассматри­ваемой точке магнитного поля.

.

Если контур с током находится в неоднородном магнитном поле, то кроме вращающего момента сил на контур будет действовать результирующая сила, отличная от нуля, втягивающая контур в область сильного поля, когда угол между магнитным моментом и вектором индукции меньше  /2.

2. Циркуляция магнитного поля ( закон полного тока ) в вакууме. Теорема Гаусса для магнитного поля.

Циркуляцией вектора магнитной индукции B называется линейный интеграл вдоль замкнутого контура L, проведённого в магнитном поле:

.

Теорема о циркуляции для магнитного поля в вакууме:

Циркуляция вектора магнитной индукции поля в вакууме равна алгебраической сумме токов, охватываемых этим контуром (т. е. результирующему току через поверхность, натянутую на контур L), умноженной на магнитную постоянную:

.

Силовые поля, для которых циркуляция силового вектора отлична от нуля, называются вихревыми или соленоидальными. Таким образом магнитное поле является вихревым, а его силовые линии (линии вектора В) замкнутыми.

Используя теорему о циркуляции можно рассчитывать магнитные поля токов, обладающие определенной симметрией, например, индукции магнитных полей внутри тороида и бесконечно длинного соленоида:

соленоида: В = ₀nI . (2.17)

тороида: B = ( ₀ / 2 )( NI / r ); R₂ < r < R₁ , (2.18)

где: n - число витков на единицу длины соленоида; N - полное число витков тороида; r - радиус окружности, лежащей внутри тороида; R₁ и R₂ - внутренний и наружный радиусы тороида; I - сила электрического тока, протекающего по соленоиду или тороиду.

Рис.2.11

Потоком вектора магнитной индукции (магнитным потоком) сквозь малую поверхность площадью dS называется физическая величина:

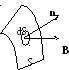
dФ _m = . (2.19)

Магнитный поток сквозь произвольную поверхность S (рис.2.11):

(2.20)

Если магнитное поле однородно, а поверхность S плоская, то

Ф _m = В _n S = BS cos(B^n) (2.21)

Единица магнитного потока в СИ-1 Вб (вебер ), 1 Вб = Тл м².

Теорема Гаусса для магнитного поля (силовые линии поля замкнуты):

Магнитный поток сквозь произвольную замкнутую поверхность равен нулю.