2. Математические модели движения морских судов

Линеаризованные математические модель МПО в общей форме могут быть представлены в матричном виде:

, ()

где A, B –матрицы связи, x –собственные координаты системы (ошибка системы, воздействие на объект, выходная координата), δ – вектор воздействия на систему (сигнал задания, помехи).

1. Модель горизонтального движения надводного судна.

Частная модель движения судна в горизонтальной плоскости при отсутствии ветро-волновых возмущений образуется дифференциальным уравнением равновесия моментов относительно вертикальной оси и уравнением связи, а также уравнением равновесия сил относительно поперечной оси. Упрощение уравнений базируется на следующих допущениях:

определяющими являются гидродинамические силы на корпусе и вертикальном руле, которые появляются в результате движения судна в невозмущенной среде;

в любой момент времени сила тяги компенсирует продольное гидродинамическое сопротивление и движение происходит с постоянной скоростью ;

в качестве технического средства управления выступает вертикальный руль, угол перекладки которого изменяется в конструктивно допустимых пределах.

Рис. 2.2. Движение судна в горизонтальной плоскости

Нормальная форма Коши имеет вид:

(2.25)

Коэффициенты в (2.25) зависят от скорости хода корабля.

В практике расчетов используются уравнения, записанные в нормированном (относительном) времени

Линеаризованные уравнения могут быть записаны в следующей матричной форме:

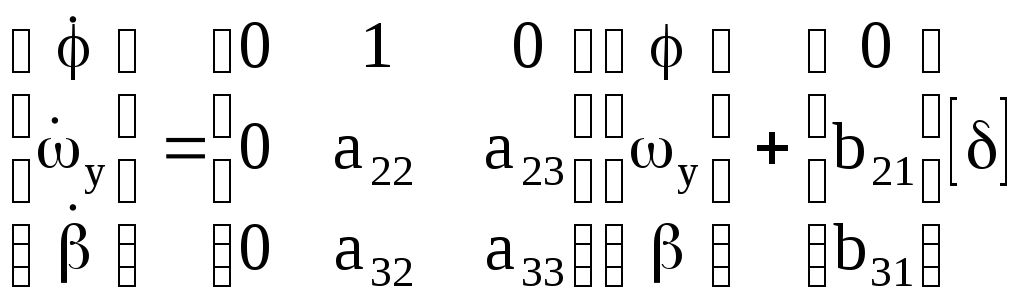(2.26)

где ,

,

,

,

,

.

Эти же уравнения могут быть выражены через скорость бокового смещения, используя известное соотношение :

(2.27)

где .

Приведенные уравнения могут быть упрощены: как правило в них пренебрегают величиной .

Таблица 2.1 Параметры модели движения водоизмещающих судов в горизонтальной плоскости

Параметр	Обозначение	Варианты судов
	единица	1	2	3	4	5	6
Объемное водоизмещение	V, м3	5315	5315	1050	520	-	2930
Длина по ватерлинии	L, м	99,6	99,6	51	39	36	75,6
Ширина по миделю	B, м	16	16	9,3	7,6	8,1	15
Осадка на миделе	Т м	5,7	4,05	4	3	2	4,5
Коэффициенты	r21	-0,58	-0,58	-0,59	-0.69	-0.46	-0,59
	r31	6,16	4,19	5,32	6,14	3,04	5,44
	q21	0,80	0,43	0,94	1,22	0,77	0,73
	q31	-7,23	-3,58	-2,41	-3,12	-0,80	-7.26
	s21	-0,34	-0,34	-0,29	-0,44	-0,18	-0.53
	s31	-3,5	-3,5	-3,4	-3,1	-1,52	-5,72
	h1	2,99	2,11	-	-	-	1,51