
- •Основные определения и понятия теории моделирования
- •Роль и место моделирования в исследовании систем
- •Задачи моделирования
- •Подходы к построению моделей
- •Классификация видов моделирования
- •Подходы в математическом моделировании
- •Требования к программно-техническим комплексам
- •Классификация пакетов моделирования
- •Концепция структурного моделирования систем
- •Структура и свойства математической модели
- •Классификация математических моделей
- •Общий подход к формированию математических моделей
- •Этапы математического моделирования
- •Основные правила построения математических моделей
- •Способы представления и оценки статических моделей
- •Парная регрессия. Оценка параметров парной регрессии.
- •Линеаризация нелинейных регрессий
- •Множественная регрессия. Оценка параметров множественной регрессии
- •Основные способы представления динамических моделей
- •Математические модели непрерывной системы
- •Представление моделей в пространстве состояний
- •Представление моделей в виде передаточных функций
- •Преобразование пф в дифференциальные уравнения
- •Интегрирующее звено
- •Апериодическое звено
- •Колебательное звено
- •Дифференцирующее звено с замедлением
- •Модели объектов управления
- •Описание математической модели дпт нв
- •Представление модели дпт нв в виде детализированной структурной схемы
- •Представление модели дпт нв в виде передаточной функции
- •Представление дпт нв в виде модели в пространстве состояний.
- •Математические модели движения морских судов
- •Модель горизонтального движения надводного судна.
- •Модель судна – модель Номото
- •Модель рулевой машины
- •Модель внешней среды
- •Моделирование дискретных систем. Преобразование непрерывных линейных систем к дискретной форме
- •Идентификация линейных дискретных систем
- •Авторегрессионные модели
- •Структуры моделей управляемого объекта
- •Спецификации моделей
- •Armax-модель
- •Постановка задачи идентификации
- •Параметрические методы идентификации
- •Метод авторегрессионной идентификации
- •Идентификация в векторно-матричной форме
- •Лабораторные работы Лабораторная работа №1. Изучение пакетов моделирования
- •Краткие сведения о среде Matlab
- •Описание среды Scilab
- •Задание на лабораторную работу
- •Лабораторная работа №2. Исследование статических зависимостей. Определение параметров парной регрессии
- •Цель работы:
- •Порядок выполнения работы
- •Содержание отчета
- •Тестовые данные
- •Контрольные задания
- •Лабораторная работа №3. Исследование статических зависимостей. Определение параметров множественной регрессии
- •Задание на лабораторную работу
- •Варианты заданий
- •Содержание отчета
- •Лабораторная работа № 5. Исследование динамических моделей линейных систем (в форме Коши и векторно-матричном виде)
- •Задание на лабораторную работу
- •Лабораторная работа № 6. Преобразование моделей (нм – дм). Исследование дискретных моделей
- •Порядок выполнения работы
- •Содержание отчета
- •Лабораторная работа № 7. Идентификация параметров динамических моделей линейных систем. Авторегрессионная идентификация
- •Задание на лабораторную работу
- •Порядок выполнения работы
- •Приложение:
- •Лабораторная работа № 8. Идентификация параметров динамических моделей линейных систем. Идентификация в пространстве состояний
- •Задание на лабораторную работу
- •Порядок выполнения работы
-
Модели объектов управления
Рассмотрим несколько примеров математических моделей объектов и систем, в частности, модели одного из широко распространенных объектов электроавтоматики – двигателя постоянного тока с независимым возбуждением (ДПТ НВ). В дальнейшем по тексту рассмотрим последовательность получения уравнений ДПТ НВ, приведение их к форме Коши, представление уравнений в виде детализированной структурной схемы (ДСС), преобразование ДСС к модели в виде передаточной функции и её упрощения. Также рассмотрены несколько моделей электромеханических систем, в которых используется ДПТ НВ как объект управления.
Наряду с электромеханическими системами в главе приведено несколько описаний моделей движения судна. Рассмотрена модель плоскопараллельного движения судна и модель, описывающая движение судна по заданному курсу.
-
Описание математической модели дпт нв
Двигатель постоянного тока независимого возбуждения (ДПТ НВ) описывается следующей системой дифференциальных и алгебраических уравнений в абсолютных единицах:
|
|
|
|
Рис. 1. ДПТ НВ и его система уравнений |
|
где
u - напряжение на якорной обмотке двигателя,
e - электродвижущая сила (ЭДС) якоря,
i - ток якоря,
Ф - поток, создаваемый обмоткой возбуждения,
M - электромагнитный момент двигателя,
MС - момент сопротивления движению,
![]() - скорость вращения
вала двигателя,
- скорость вращения
вала двигателя,
R - активное сопротивление якорной цепи,
L - индуктивность якорной цепи,
J - суммарный момент инерции якоря и нагрузки,
![]() - коэффициент связи
между скоростью и ЭДС,
- коэффициент связи
между скоростью и ЭДС,
СМ - коэффициент связи между током якоря и электромагнитным моментом.
Определение области принадлежности переменных.
С точки зрения
будущей модели, входными воздействиями
являются напряжения якоря u и момент
сопротивления движению MС, выходными
переменными - электромагнитный момент
двигателя M и скорость вращения вала
двигателя
![]() ,
а переменными состояния - переменные
стоящие под знаком производной: ток
якоря i и скорость вращения вала двигателя
,
а переменными состояния - переменные
стоящие под знаком производной: ток
якоря i и скорость вращения вала двигателя
![]() .
Остальные переменные, входящие в состав
уравнений (1.1) - (1.4) являются параметрами,
численные значения которых, необходимо
будет задавать при проведении расчетов.
.
Остальные переменные, входящие в состав
уравнений (1.1) - (1.4) являются параметрами,
численные значения которых, необходимо
будет задавать при проведении расчетов.
Преобразуем дифференциальные уравнения (1.1) и (1.2) к явной форме Коши и выполним подстановку. Система уравнений примет вид:
![]() (1.5)
(1.5)
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
Последнее уравнение есть отражение того факта, что переменная состояния является также и выходной переменной.
-
Представление модели дпт нв в виде детализированной структурной схемы
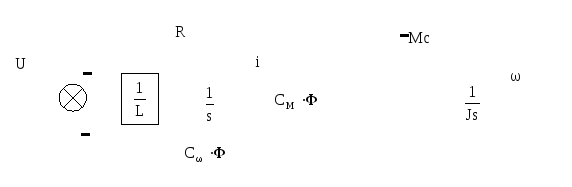
-
Представление модели дпт нв в виде передаточной функции
Преобразование детализированной структурной схемы дает промежуточный результат:
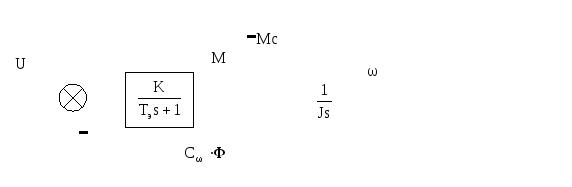 ,
,
Где коэффициент
![]() ,
электрическая постоянная времени
,
электрическая постоянная времени
![]() ,
и окончательный, при
,
и окончательный, при
![]()
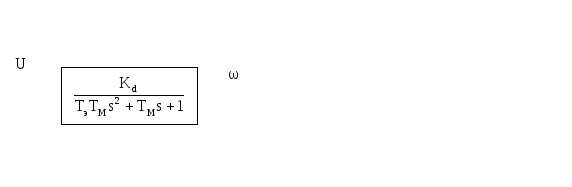
Где коэффициент
передачи двигателя
![]() ,
механическая постоянная времени
,
механическая постоянная времени
![]() .
.
-
Представление дпт нв в виде модели в пространстве состояний.
Для составления модели в пространстве состояний введем "машинные" переменные:
входные переменные:
![]() ,
,
![]() ;
;
выходные переменные:
![]() ,
,
![]() ;
;
переменные
состояния:
![]() ,
,
![]() .
.
Тогда уравнения (1.5) - (1.8) примут вид:
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
Перепишем систему уравнений (1.9) – (1.12) в матричной форме:
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
-
 ,
, ,
,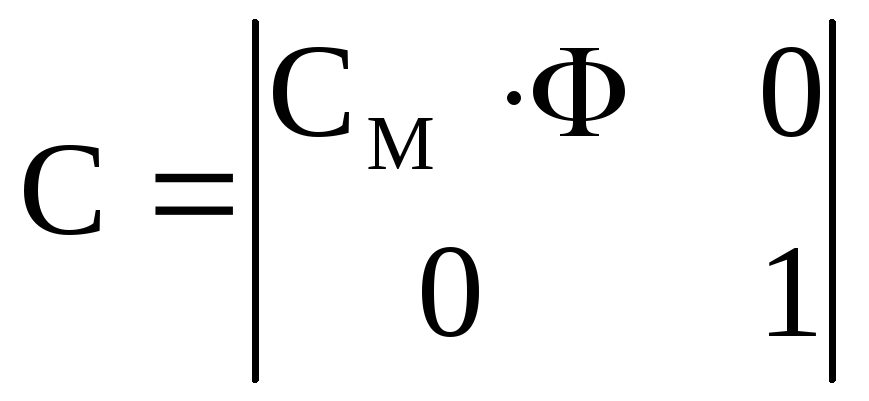 ,
,
 ,
,

