
- •1. Пределы и их свойства
- •2. Дифференцирование функции одной переменной
- •3. Интегральное исчисление
- •3.1. Первообразная и неопределенный интеграл
- •1. Непосредственное интегрирование.
- •2. Метод подстановки.
- •3. Метод интегрирования по частям.
- •3.2. Определенный интеграл
- •Формулы площадей плоских фигур.
- •2. Формулы объемов тел вращения.
- •4. Дифференциальные уравнения и их применение в медицинской практике
- •5. Основы теории вероятностей
- •Виды случайных событий
- •Полная группа событий
- •Исходы испытания
- •Классическое определение вероятности
- •Статистическое определение вероятности
- •Решение:
- •Решение:
- •Решение:
- •6. Случайные величины и их числовые характеристики
- •6.1. Дискретная случайная величина
- •Свойства математического ожидания
- •Свойства дисперсии
- •Решение:
- •6.2. Непрерывная случайная величина
- •Числовые характеристики непрерывной случайной величины Математическое ожидание
- •Среднее квадратическое отклонение
- •Решение:
- •6.3. Нормальное распределение непрерывной случайной величины (закон Гаусса)
- •7. Элементы математической статистики
- •Оценка параметров генеральной совокупности
- •Литература
- •Содержание
2. Формулы объемов тел вращения.
Рассмотрим некоторое тело и вычислим его объем. Допустим, что известны площади сечений этого тела плоскостями, перпендикулярными оси Ох. С изменением х площадь сечения также будет изменяться, т. е. являться некоторой функцией х. Обозначим эту функцию через S(x) и будем считать ее непрерывной функцией на отрезке [a, b]. Тогда объем тела
![]()
В частном случае,
когда тело образовано вращением вокруг
оси Ox
и криволинейной
трапеции, заданной непрерывной функцией
![]() ,
объем тела вращения вычисляется по
формуле
,
объем тела вращения вычисляется по
формуле
![]() (3)
(3)
Если криволинейная
трапеция
![]() вращает вокруг оси Oy,
то объем тела вращения
вращает вокруг оси Oy,
то объем тела вращения
![]() (4)
(4)
Пример: Вычислить объем шара радиуса R.
Решение:
Шар радиуса R
получается вращением полуокружности
![]() вокруг оси Ox,
поэтому его объем V
можно найти по формуле (3). Используя
симметрию данного шара относительно
оси Oy,
находим
вокруг оси Ox,
поэтому его объем V
можно найти по формуле (3). Используя
симметрию данного шара относительно
оси Oy,
находим
![]()
Решение типовых задач
Задание1.
Найти первообразные для функций
![]() .
.
Решение:
-
Функция
 Легко
заметить, что
Легко
заметить, что
 имеет ту же самую производную
имеет ту же самую производную
 и поэтому также является первообразной
для
и поэтому также является первообразной
для
 на R.
Ясно, что вместо числа 7 можно поставить
любую постоянную. Таким образом, мы
видим, что задача нахождения первообразной
имеет бесконечно много решений.
на R.
Ясно, что вместо числа 7 можно поставить
любую постоянную. Таким образом, мы
видим, что задача нахождения первообразной
имеет бесконечно много решений. -
Для функции
 на интервале (0; +)
первообразной является функция
на интервале (0; +)
первообразной является функция
 ,
так как
,
так как
 для всех x
из этого
интервала. Так же как и в примере 1,
функция
для всех x
из этого
интервала. Так же как и в примере 1,
функция
 при любой постоянной С есть первообразная
для функции
при любой постоянной С есть первообразная
для функции
 на том же интервале (0; +).
на том же интервале (0; +). -
Функция
 не является первообразной для функции
не является первообразной для функции
 на промежутке
на промежутке
 ,
так как равенство
,
так как равенство
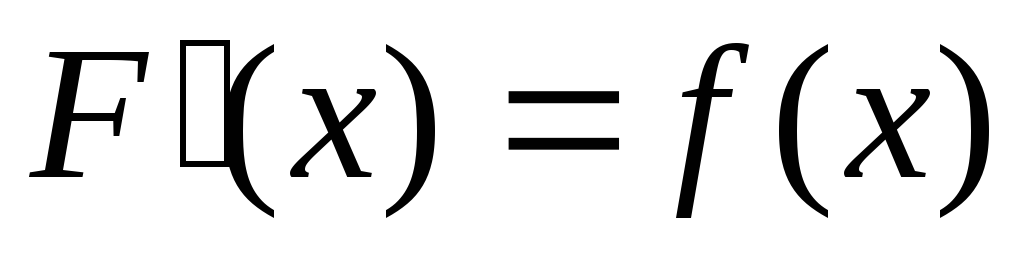 не выполнено в точке 0. Однако в каждом
из промежутков
не выполнено в точке 0. Однако в каждом
из промежутков
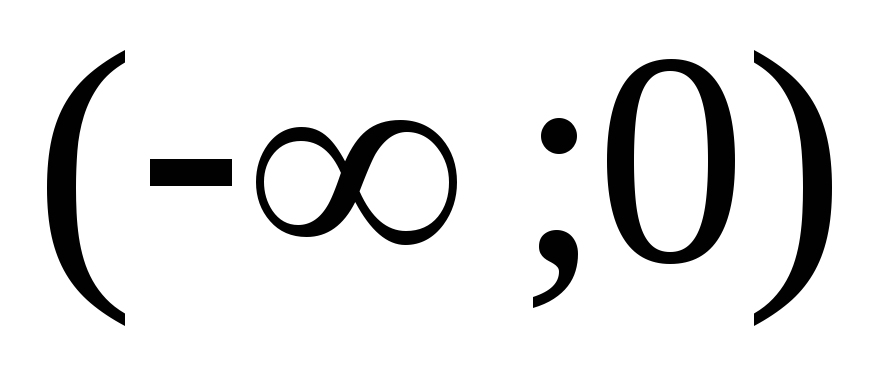 и
и
 функция F
является первообразной для f.
функция F
является первообразной для f.
Задание 2. Вычислить интегралы:

Решение:



Задание 3.
1) Вычислить работу,
совершенную одним молем идеального
газа при обратном изотермическом
расширении от
![]()
Решение: При
обратимом расширении одного моля
идеального газа давление
![]() Совершаемая газом при изменении объема
на величину dV
элементарная работа dA=pdV.
Полная
работа расширения газа от начального
объема V1
до конечного
объема V2
Совершаемая газом при изменении объема
на величину dV
элементарная работа dA=pdV.
Полная
работа расширения газа от начального
объема V1
до конечного
объема V2
 2)
Скорость поступательно движущегося
тела
2)
Скорость поступательно движущегося
тела
![]() (м/с). Определить путь, пройденный телом
за первые 10с после начала движения.
(м/с). Определить путь, пройденный телом
за первые 10с после начала движения.
Решение: Так как
![]() то
то
![]() откуда
откуда

В нашем случае t1=0, t2=10, v=8t-1.
Искомый путь
![]()
Упражнения
Задание 1. Вычислить интегралы
Задание 2. Решить задачи
-
Найти функцию, производная от которой равна
 и при
и при
 принимает значение, равное 4.
принимает значение, равное 4. -
Найти функцию, производная которой равна
 а при х=1
значение функции равно 2е.
а при х=1
значение функции равно 2е. -
Составить уравнение пути
 если скорость тела задана формулой
если скорость тела задана формулой
 (м/c)
и за t=3
с тело прошло путь s=60
м.
(м/c)
и за t=3
с тело прошло путь s=60
м. -
Составить уравнение движения точки, если скорость точки
 (м/c),
а при t=0
точка покоилась.
(м/c),
а при t=0
точка покоилась. -
Составить уравнение движения точки, если скорость точки
 (м/c),
а при t=1
с s=3e
м.
(м/c),
а при t=1
с s=3e
м.
-
Материальная точка движется прямолинейно. Ускорение точки изменяется по закону
 ,
где
,
где
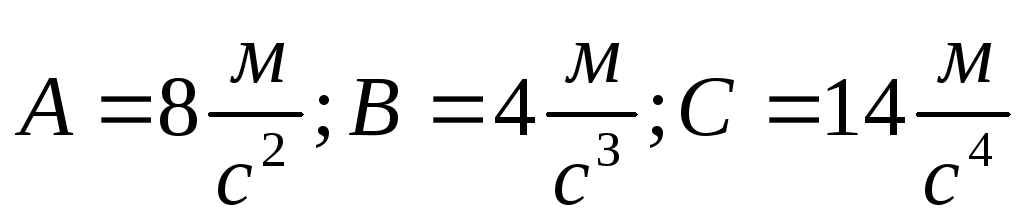 .
Какой скорости достигнет материальная
точка через
.
Какой скорости достигнет материальная
точка через
 после начала движения из состояния
покоя? Какой путь пройдет она за это
время?
после начала движения из состояния
покоя? Какой путь пройдет она за это
время? -
Задан закон изменения углового ускорения
 .
Какой угловой скорости
.
Какой угловой скорости
 достигнет материальная точка через
достигнет материальная точка через
 после
начала движения из состояния покоя?
Чему равно ее угловое перемещение
после
начала движения из состояния покоя?
Чему равно ее угловое перемещение
 за это время?
за это время? -
Тело движется прямолинейно с ускорением
 .
Найти скорость тела в момент
.
Найти скорость тела в момент
 и
закон движения тела, если в начальный
момент тело находилось в начале
координат и начальная скорость тела
равна нулю.
и
закон движения тела, если в начальный
момент тело находилось в начале
координат и начальная скорость тела
равна нулю. -
Две точки начинают двигаться по прямой в один и тот же момент времени в одном и том же направлении из одного и того же места. Скорости точек равны
 м/с,
м/с,
 м/с соответственно. Через какое время
расстояние между ними составит 216 м?
м/с соответственно. Через какое время
расстояние между ними составит 216 м? -
Тело движется прямолинейно со скоростью
 Найти путь, пройденный телом от начала
движения до остановки.
Найти путь, пройденный телом от начала
движения до остановки. -
Ускорение протона изменяется по закону:
 (в
СИ). Найти: 1) законы движения
(в
СИ). Найти: 1) законы движения
 2) соотношения между
2) соотношения между
 и
и
 .
. -
Найти массу стержня длинной 100см, если его линейная плотность изменяется по закону:
 .
. -
Какое количество тепла выделится в проводнике сопротивлением
 за 60 секунд, если ток изменяется по
закону:
за 60 секунд, если ток изменяется по
закону:
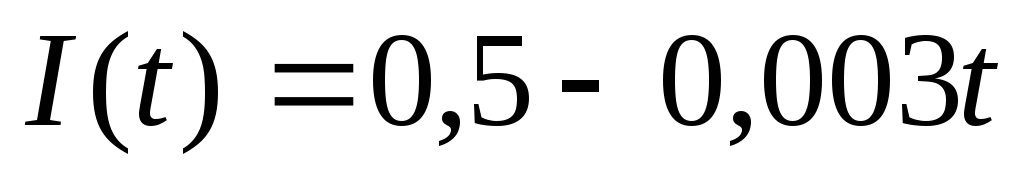 (в
СИ). (Указание:
(в
СИ). (Указание:
 ,
,
 –количество
теплоты).
–количество
теплоты). -
В момент времени t скорость изменения концентрации препарата с изотопным индикатором изменяется по закону:
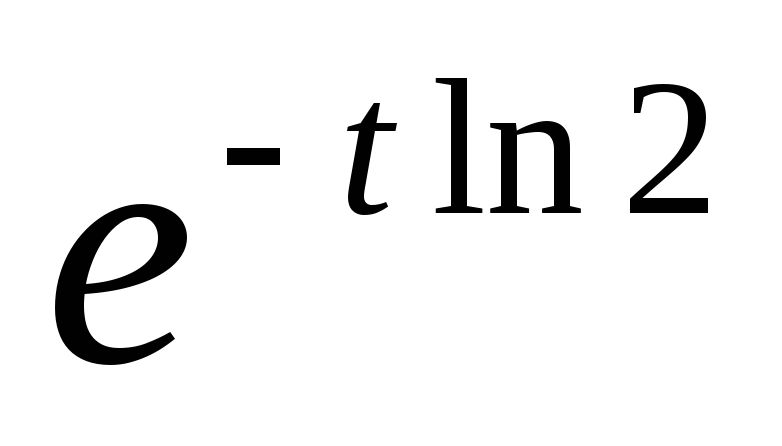 .
Найти концентрацию препарата в момент
времени
.
Найти концентрацию препарата в момент
времени

-
На материальную точку действует сила, которая линейно зависит от пройденного пути:
 .
В начале движения она составляет 100Н,
а когда точка переместилась на 10м,
сила возросла до 600Н. Найти работу,
произведенную силой на этом пути.
Указание: элементарная работа
.
В начале движения она составляет 100Н,
а когда точка переместилась на 10м,
сила возросла до 600Н. Найти работу,
произведенную силой на этом пути.
Указание: элементарная работа
 .
. -
Вычислить работу, совершаемую при сжатии пружины на 15см, если известно, что для сжатия пружины на 1см необходима сила 30Н. (Указание:
 ).
).
-
Тело движется прямолинейно со скоростью
 .
Найти значение
.
Найти значение
 если известно, что за время от 0 до 2с
тело прошло путь длиной 40м.
если известно, что за время от 0 до 2с
тело прошло путь длиной 40м. -
Тело движется со скоростью
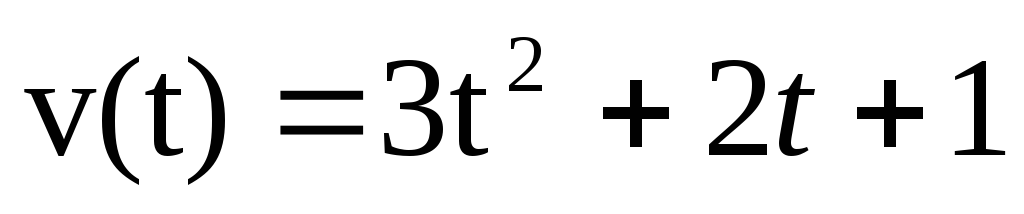 (м/с).
Найти путь, пройденный телом за время
от
(м/с).
Найти путь, пройденный телом за время
от
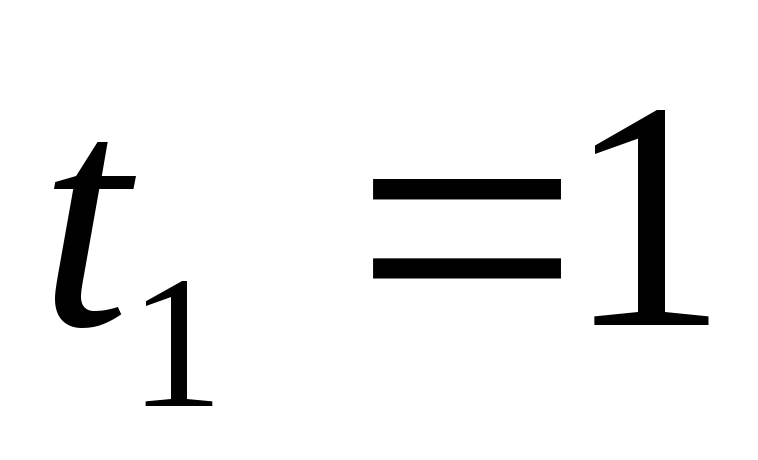 c
до
c
до
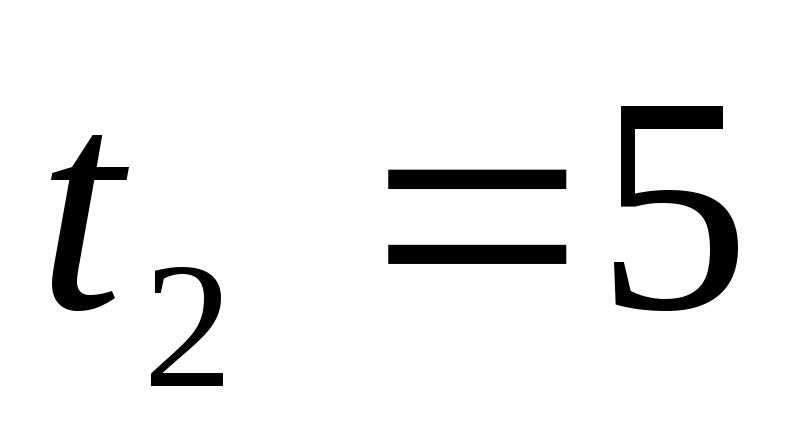 c.
c. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Найти, при каком значении
 площадь фигуры, ограниченной кривой
площадь фигуры, ограниченной кривой
 прямыми
прямыми
 и осью абсцисс, равна
и осью абсцисс, равна
 .
. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок. -
Вычислить площадь фигуры, ограниченной линиями:
 .
Сделать рисунок.
.
Сделать рисунок.










