3. Метод интегрирования по частям.

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

Теорема. Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть функция имеет первообразную на этом промежутке, т. е. существует . Тогда на промежутке Х функция также имеет первообразную и справедлива формула

(1)

Так как то формулу (1) можно записать в виде

Вычислить интегралы:

Проверка:

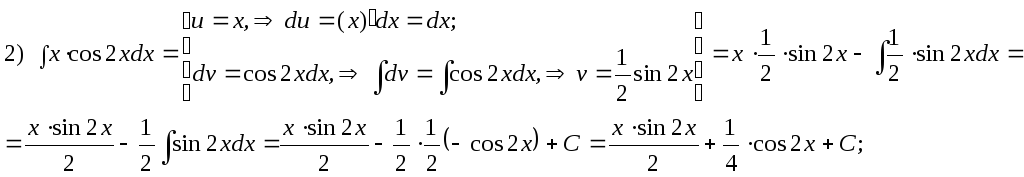
Проверка:

Проверка:

3.2. Определенный интеграл

Определение определенного интеграла.

Пусть функция определена на отрезке [a, b], a<b. Разобьем этот отрезок на n произвольных частей точками a=x₀<x₁<x₂<…<x_i-1<x_i<…<x_n=b. В каждом из полученных частичных отрезков [x_i-1, x_i] выберем произвольную точку и составим сумму

(1)

где Сумма вида (1) называется интегральной суммой для функции f(x) на [a, b].

Обозначим через  длину наибольшего частичного отрезка разбиения: .

Определение. Если существует конечный предел I интегральной суммы (1) при , то этот предел называется определенным интегралом от функции f(x) по отрезку [a, b] и обозначается следующим образом:

В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х – переменной интегрирования.

Для интегрируемости функции достаточно ее непрерывности на отрезке [a, b].

Основные свойства определенного интеграла.

1. По определению,

2. По определению,

3. Каковы бы ни были числа a, b, c, всегда имеет место равенство

4. Постоянный множитель можно выносить за знак определенного интеграла, т. е.

5. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т. е.

Формула Ньютона – Лейбница.

Если функция f(x) непрерывна на отрезке [a, b] и функция F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница

Некоторые физические и геометрические приложения определенного интеграла

1. Формулы площадей плоских фигур.

a) Пусть на плоскости Оxy дана фигура, ограниченная отрезком [a, b] оси Ox, прямыми x=a, x=b и графиком непрерывной и неотрицательной функции y=f(x) на [a, b]. Такую фигуру называют криволинейной трапецией, площадь S которой может быть вычислена по формуле

(1)

Пример:

1) Найти площадь фигуры, ограниченной линиями

Решение:

Рис. 1.

Можно считать, что эта фигура ограничена осью Ох, прямыми х=-1, х=1 и графиком функции (рис.1), поэтому по формуле (1), ее площадь

2) Найти площадь фигуры, ограниченной линиями

Решение:

Рис. 2.

Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную осью абсцисс, прямыми х=0 и х=3 графиком функции, которая на отрезке [0, 1] равна х, а на отрезке [1, 3] равна Разобьем данную криволинейную трапецию прямой х=1 на две части (рис. 2). Площади этих частей находятся по формуле (1):

Площадь искомой криволинейной трапеции находим согласно свойству аддитивности площади,

b) Пусть на отрезке [a, b] заданы две непрерывные функции причем при всех значениях х из этого отрезка . Площадь данной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций прямыми х=а и х=b и осью абсцисс. Следовательно, площадь S данной фигуры можно найти так:

(2)

Пример:

1) Найти площадь фигуры, ограниченной графиками функций (рис. 3).

Решение:

Рис. 3.

Пределами интегрирования являются абсциссы точек пересечения графиков данных функций. Найдем их. Для этого решим систему уравнений

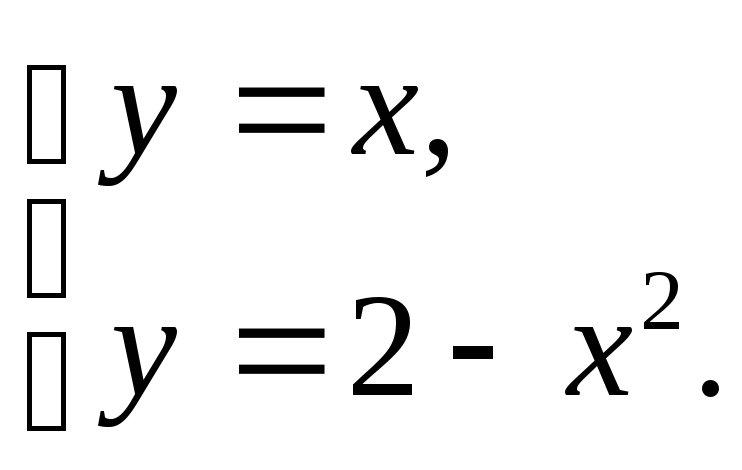
В результате получаем Искомую площадь находим с помощью формулы (2):

2) Найти площадь фигуры, ограниченной линиями

Решение:

Рис. 4.

Данная фигура заключена между графиками функций , прямыми х=0, х=1 (рис. 4). Поэтому ее площадь находим с помощью формулы (2):