Упражнения и задания для самостоятельной работы
Теоретические вопросы
-
Что называется пределом числовой последовательности?
-
Что такое бесконечно малая (бесконечно большая) величина?
-
Какие свойства пределов числовых последовательностей используют при вычислении пределов?
-
Что такое предел функции в точке?
-
Какие свойства пределов функций используются при вычислении пределов?
-
Что такое I (II) замечательный предел?
Задача 1 . Вычислить пределы функций.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задача 2. Вычислить пределы числовых последовательностей.
1.
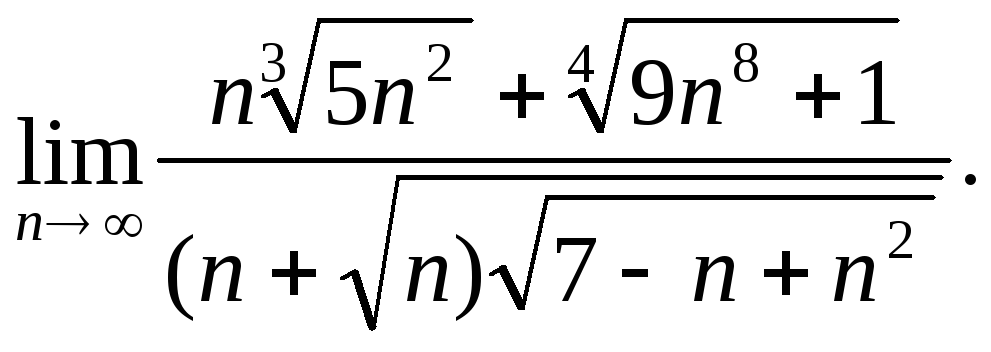
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задача
3 . Доказать (найти
),
что:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
Задача 4. Вычислить пределы функций.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
Задача 5. Вычислить предел функции или числовой последовательности.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
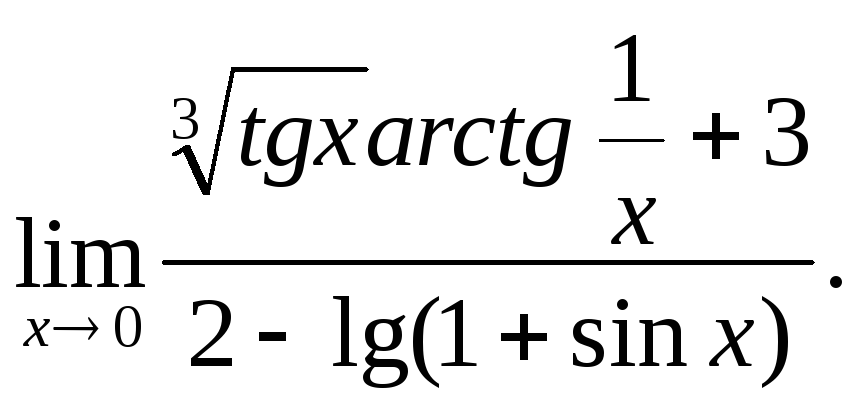
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
-
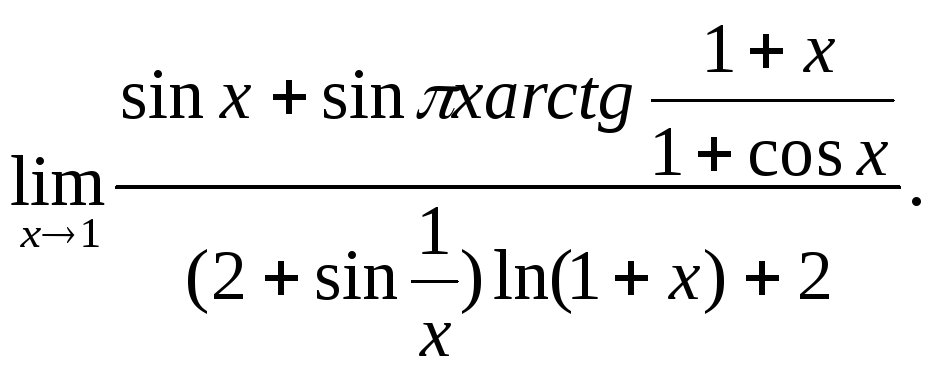
Непрерывность функции
Приращения аргумента и функции
Пусть
есть некоторое значение данной переменной
величины. Наряду с
рассмотрим другое значение
этой переменной величины.
Определение. Приращением переменной величины называется разность между новым значением этой величины и ее прежним значением, т.е. приращение переменной величины равно
.
Для обозначения приращения используется
греческая буква
.
Например,
обозначает приращение величины
.
Предположим, что
есть
некоторая функция от аргумента
,
т.е.
.
Дадим аргументу
приращение
;
тогда
получит соответствующее приращение
.
Этот факт можно записать так:
.
Из двух последних равенств следует
.
Определение. Функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Определение. Функция
называется непрерывной на данном
множестве
,
если:
-
она определена на этом множестве;
-
непрерывна в каждой точке этого множества.
Определение. Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции.