
- •Федеральное государственное образовательное учреждение среднего профессионального образования Красноярский юридический техникум
- •Пояснительная записка
- •Функция Понятие функции. Способы задания и свойства
- •Решение типовых заданий
- •Упражнения и задания для самостоятельной работы
- •Предел функции. Методы вычисления пределов функции.
- •Основные теоремы о пределах
- •Решение типовых заданий
- •Упражнения и задания для самостоятельной работы
- •Непрерывность функции
- •Односторонние пределы Скачок функции
- •Раскрытие неопределенностей
- •Решение типовых заданий
- •Упражнения и задания для самостоятельной работы Теоретические вопросы
- •Задание 1. Доказать, что функция непрерывна в точке (найти ).
- •Задание 3. Вычислить пределы функции.
- •Задача 5. Вычислить пределы функций.
- •Задача 6. Вычислить пределы функций.
- •Список рекомендуемой литературы
Основные теоремы о пределах
Теорема 1. Если каждое слагаемое
алгебраической суммы конечного числа
функций имеет предел при
![]() ,
то предел этой алгебраической суммы
при
,
то предел этой алгебраической суммы
при
![]() существует и равен такой же алгебраической
сумме пределов слагаемых.
существует и равен такой же алгебраической
сумме пределов слагаемых.
![]() .
.
Терема 2. Если каждый из
сомножителей произведения конечного
числа функций имеет предел при
![]() ,
то предел произведения при
,
то предел произведения при
![]() равен произведению пределов сомножителей.
равен произведению пределов сомножителей.
![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела.
![]() .
.
Следствие 2. Если функция
![]() имеет предел при
имеет предел при
![]() ,
то предел при
,
то предел при
![]() целой положительной степени ее равен
такой же степени предела этой функции,
т.е.
целой положительной степени ее равен
такой же степени предела этой функции,
т.е.
![]() ,
(n – натуральное число).
,
(n – натуральное число).
Теорема 3. Если функция
![]() имеет предел при
имеет предел при
![]() ,
отличный от нуля, то предел при
,
отличный от нуля, то предел при
![]() обратной
ей по величине функции
обратной
ей по величине функции
![]() равен обратной величине предела данной
функции, т.е.
равен обратной величине предела данной
функции, т.е.
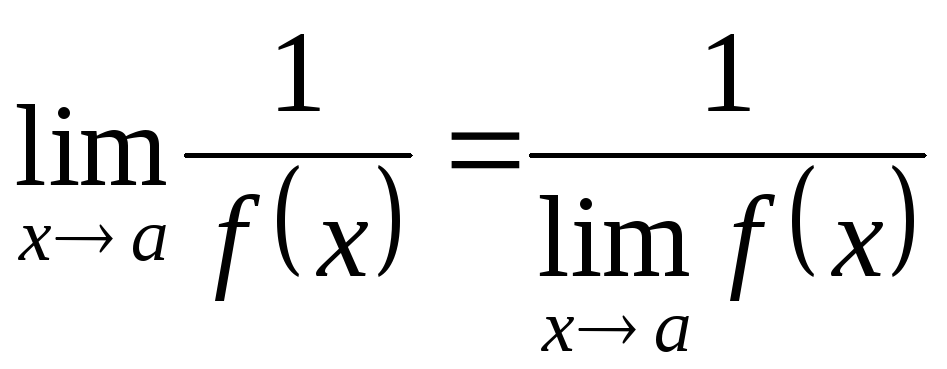 .
.
Теорема 4. Если делимое
![]() и делитель
и делитель
![]() имеют пределы при
имеют пределы при
![]() и предел делителя отличен от нуля, то
предел их частного (дроби) при
и предел делителя отличен от нуля, то
предел их частного (дроби) при
![]() равен частному пределов делимого
(числителя дроби) и делителя (знаменателя
дроби), т.е.
равен частному пределов делимого
(числителя дроби) и делителя (знаменателя
дроби), т.е.
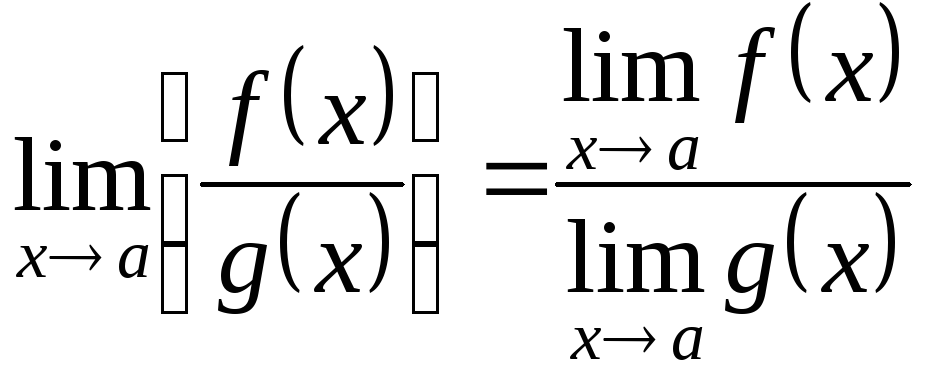 .
.
Теорема 5. Если функция
![]() имеет предел при
имеет предел при
![]() и
и
![]() (n – натуральное число)
существует в точке
(n – натуральное число)
существует в точке
![]() и в некоторой ее окрестности, то
и в некоторой ее окрестности, то
![]() .
.
Решение типовых заданий
Пример
1.
Найти: а)
![]() ;
б) ; в) ; г) .
;
б) ; в) ; г) .
Р е ш е н и е: а) На основании непрерывности
функции в точке х=7 искомый предел равен
значению функции в этой точке, т.е.
![]() .
.
б) При
![]() числитель
(3х+5) стремится к
числитель
(3х+5) стремится к
![]() (т.е. является ограниченной функцией),
а знаменатель (х-5) – к нулю (т.е. является
бесконечно малой величиной); очевидно,
их отношение есть величина бесконечно
большая, т.е.
(т.е. является ограниченной функцией),
а знаменатель (х-5) – к нулю (т.е. является
бесконечно малой величиной); очевидно,
их отношение есть величина бесконечно
большая, т.е.
![]() =
=![]() .
.
в)
![]() =0,
ибо отношение ограниченной функции
sinx
=0,
ибо отношение ограниченной функции
sinx
![]() к бесконечно большой величине х (при )
есть величина бесконечно малая.
к бесконечно большой величине х (при )
есть величина бесконечно малая.
г)
![]() =0,
т.к. произведение бесконечно малой
величины х (при
=0,
т.к. произведение бесконечно малой
величины х (при![]() )
на ограниченную функцию
)
на ограниченную функцию
![]() есть величина бесконечно малая.
есть величина бесконечно малая.
Заметим, что этот предел нельзя вычислять
с помощью теоремы о пределе произведения,
поскольку
![]() не существует (при
не существует (при
![]() аргумент косинуса
аргумент косинуса
![]() изменяется непрерывно вдоль числовой
оси до бесконечности, при этом значения
изменяется непрерывно вдоль числовой
оси до бесконечности, при этом значения
![]() колеблются от -1 до 1 и от 1 до -1, не стремясь
ни к какому числу (пределу).
колеблются от -1 до 1 и от 1 до -1, не стремясь
ни к какому числу (пределу).
В рассмотренных примерах предел
находится сразу: в виде числа или символа
![]() .
Но чаще при вычислении пределов мы
сталкиваемся с неопределенностями,
когда результат нахождения предела
неясен: например, в случае отношения
двух бесконечно малых функций (условное
обозначение
.
Но чаще при вычислении пределов мы
сталкиваемся с неопределенностями,
когда результат нахождения предела
неясен: например, в случае отношения
двух бесконечно малых функций (условное
обозначение
![]() )
или бесконечно больших
)
или бесконечно больших
![]() .
Кроме отмеченных неопределенностей
вида
.
Кроме отмеченных неопределенностей
вида
![]() и в математическом анализе рассматриваются
также неопределенности вида
и в математическом анализе рассматриваются
также неопределенности вида
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Пример 2. Найти:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Р е ш е н и е: а) для раскрытия неопределенности
вида
![]()
Разложим числитель на множители и
сократим дробь множитель (х-1): сокращение
возможно, т.к. при
![]() (х-1) стремится к нулю, но не равен нулю.
(х-1) стремится к нулю, но не равен нулю.
![]() =
=![]() =
=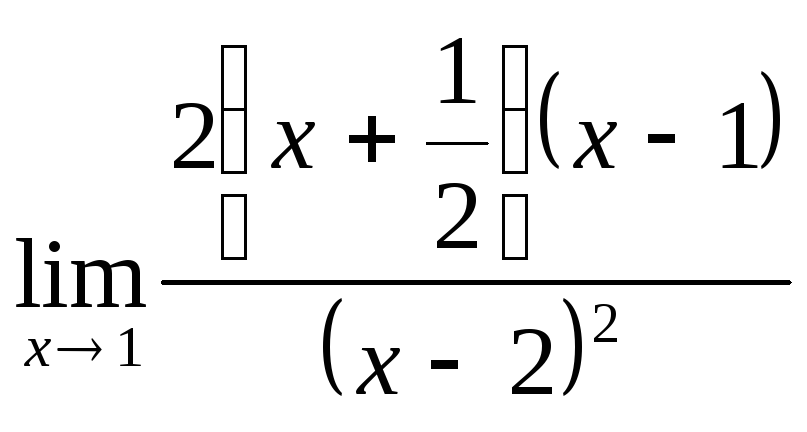 =
=![]() .
.
б) Для раскрытия неопределенности вида
![]() умножим числитель и знаменатель на
выражение, сопряженное к числителю,
получим:
умножим числитель и знаменатель на
выражение, сопряженное к числителю,
получим:
![]() в)
Для раскрытия неопределенности вида
в)
Для раскрытия неопределенности вида
![]() удобно предварительно сделать замену
удобно предварительно сделать замену
![]() (тогда
(тогда
![]() , при
, при
![]() ), а затем полученные многочлены разложить
на множители:
), а затем полученные многочлены разложить
на множители:
![]() =
=![]() =
=![]() .
.
Пример 3. Найти: а)
![]() ;
б)
;
б)
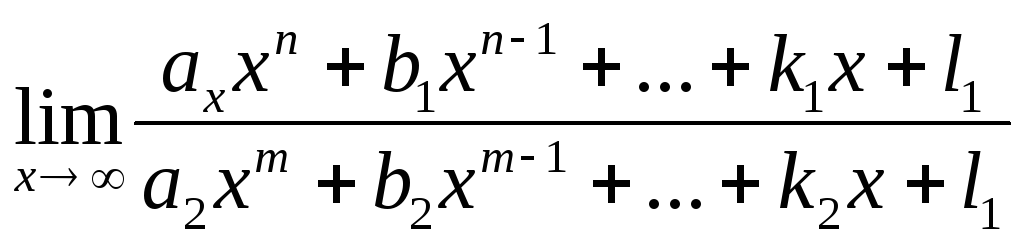 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
Р е ш е н и е: а) Имеем неопределенность
вида
![]() .
Учитывая, что поведение числителя и
знаменателя при
.
Учитывая, что поведение числителя и
знаменателя при
![]() определяется членами с наибольшими
показателями степеней (соответственно
определяется членами с наибольшими
показателями степеней (соответственно
![]() и
и
![]() ),
разделим числитель и знаменатель на
),
разделим числитель и знаменатель на
![]() ,
т.е. на х с наибольшим показателем
степени числителя и знаменателя.
Используя теоремы о пределах, получим:
,
т.е. на х с наибольшим показателем
степени числителя и знаменателя.
Используя теоремы о пределах, получим:
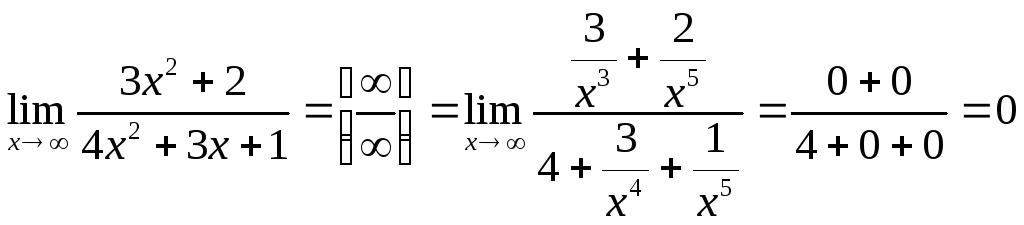 .
.
б) Используя тот же прием, что и в п.а), можно показать, что
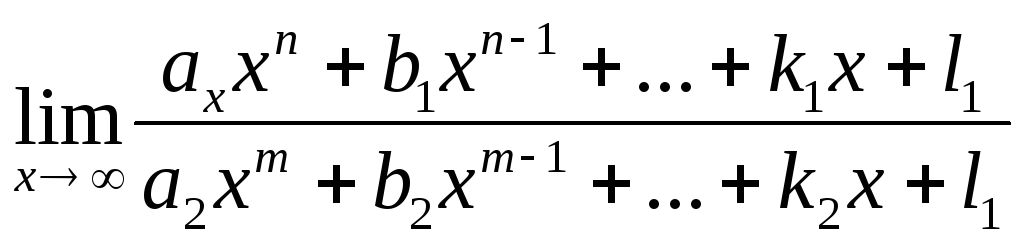 =
=![]() =
=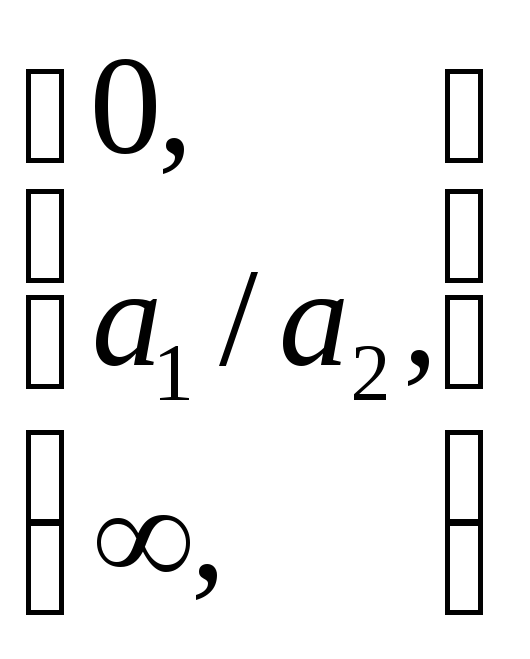 ,
т.е. предел отношения двух многочленов
,
т.е. предел отношения двух многочленов
![]() равен 0, отношению коэффициентов при
старших степенях х или
равен 0, отношению коэффициентов при
старших степенях х или
![]() ,
если показатель степени числителя и
соответственно меньше, равен или больше
показателя степени знаменателя m.
,
если показатель степени числителя и
соответственно меньше, равен или больше
показателя степени знаменателя m.
Рекомендуем запомнить это правило.
в) Имеем неопределенность вида
![]() .
Здесь выражению в числителе условно
можно приписать степень
.
Здесь выражению в числителе условно
можно приписать степень
![]() ,
а в знаменателе степень m=2;
т.к.
,
а в знаменателе степень m=2;
т.к.
![]() ,
то на основании правила, сформулированного
в п.б), искомый предел равен
,
то на основании правила, сформулированного
в п.б), искомый предел равен
![]() .
.
Действительно, разделив и числитель и
знаменатель на
![]() ,
получим:
,
получим:
![]() =
=![]() =
=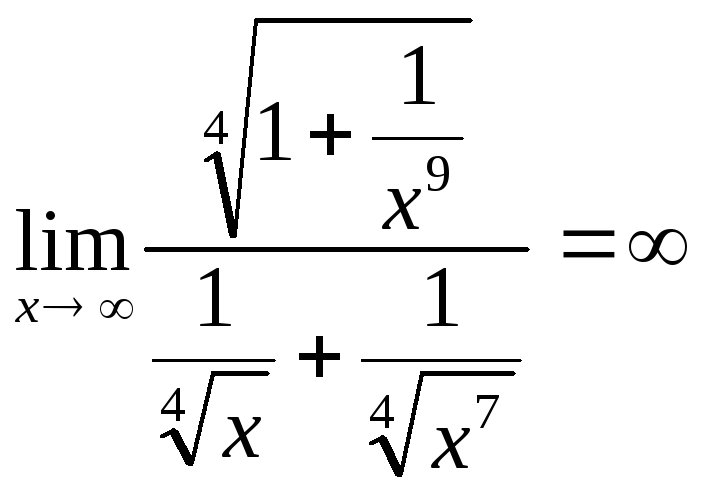 .
.
г) При
![]() имеем неопределенность вида
имеем неопределенность вида
![]() ,
при этом поведение числителя и знаменателя
определяется вторыми слагаемыми,
которые возрастают быстрее первых.
Разделив числитель и знаменатель на
,
при этом поведение числителя и знаменателя
определяется вторыми слагаемыми,
которые возрастают быстрее первых.
Разделив числитель и знаменатель на
![]() и используя теоремы о пределах, получим:
и используя теоремы о пределах, получим:
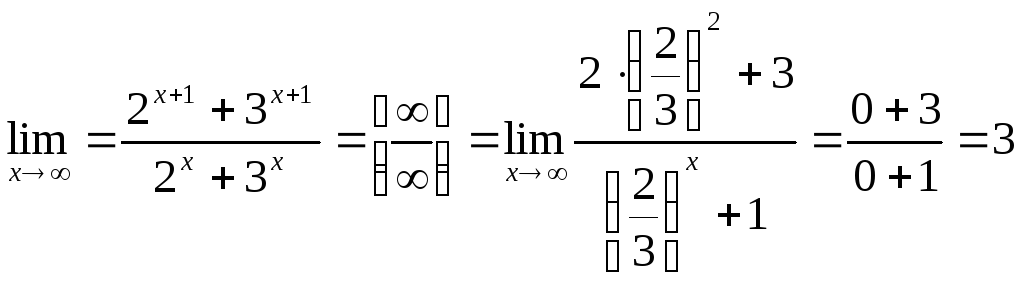 ,
поскольку
,
поскольку
![]() .
.
При
![]() имеем неопределенность вида
имеем неопределенность вида
![]() ,
при этом поведение числителя и знаменателя
определяется первыми слагаемыми,
которые убывают медленнее других.
Разделив числитель и знаменатель на
,
при этом поведение числителя и знаменателя
определяется первыми слагаемыми,
которые убывают медленнее других.
Разделив числитель и знаменатель на
![]() и используя теоремы о пределах, получим:
и используя теоремы о пределах, получим:
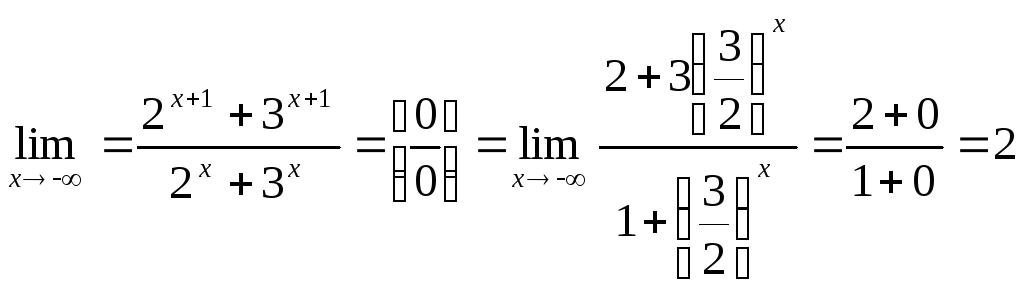 .
.
д) Для раскрытия неопределенности вида разделим числитель на x, получим
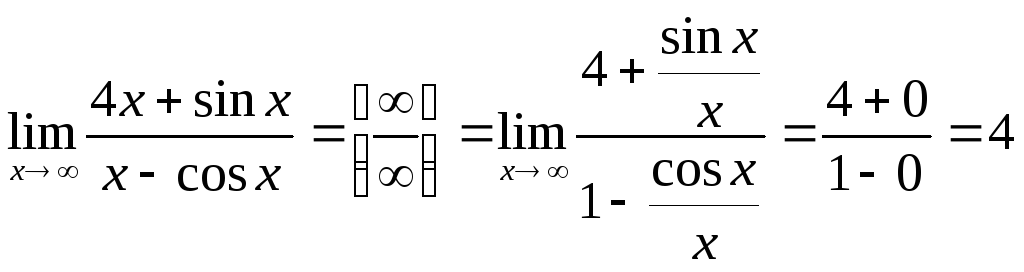
так как![]()
![]()
Пример 4. Найти:
а)
![]()
б)
![]()
в)
![]()
Решение: а) Для раскрытия неопределенности вида умножим и разделим выражение в скобках на сопряжение выражение, получим
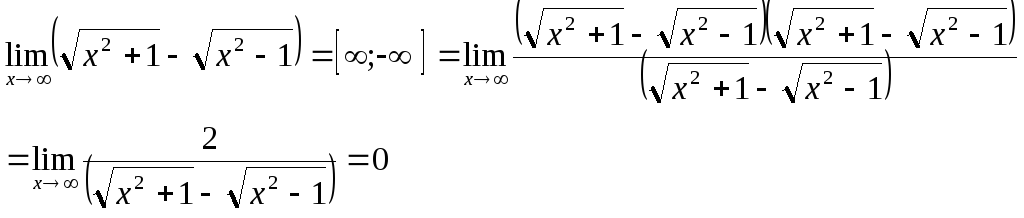
б) При
![]() имеем
неопределенность вида , ибо квадратный
корень из неотрицательного числа всегда
неотрицателен.
имеем
неопределенность вида , ибо квадратный
корень из неотрицательного числа всегда
неотрицателен.
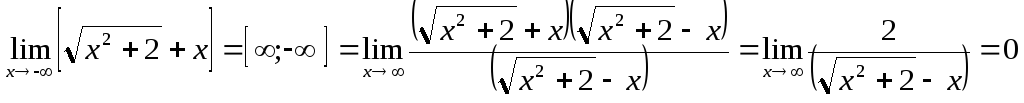
Обращаем внимание на то, что при x
→ ![]() в знаменателе нет неопределенности,
так как он представляет сумму бесконечно
больших положительных величин –
величину, бесконечно большую.
в знаменателе нет неопределенности,
так как он представляет сумму бесконечно
больших положительных величин –
величину, бесконечно большую.
в)
![]()
Пример 5. Вычислить пределы числовых последовательностей.
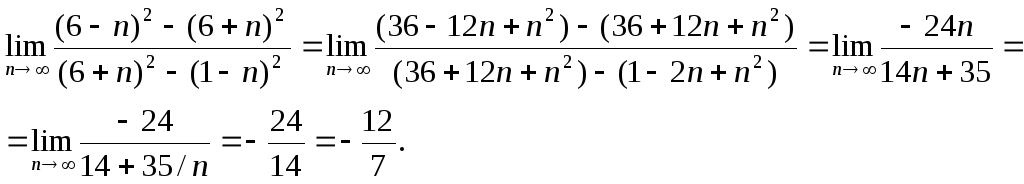
Пример 6. Вычислить пределы числовых последовательностей.
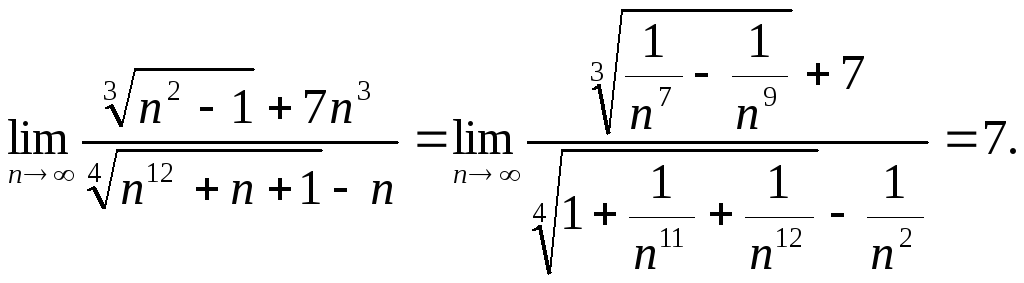
Пример 7 . Вычислить пределы функций.
![]()
Пример 8 . Вычислить пределы функций.
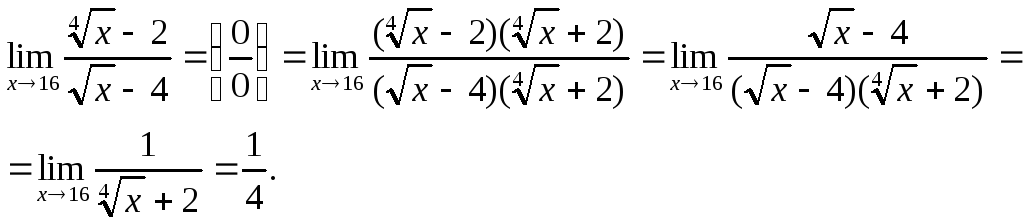
Пример 9 . Вычислить пределы функций.
![]()
Пример 10. Вычислить пределы функций.
![]()
Пример 11. Вычислить пределы функций.
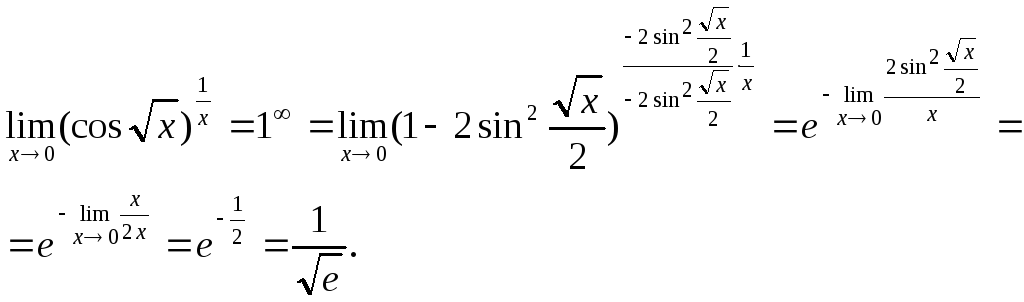
Пример 12. Вычислить пределы функций.
![]()
Пример 13. Вычислить пределы функций.
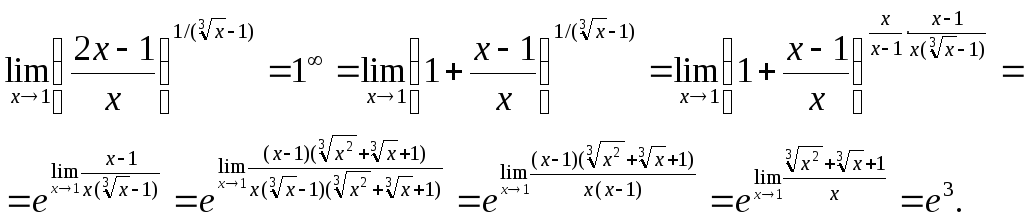
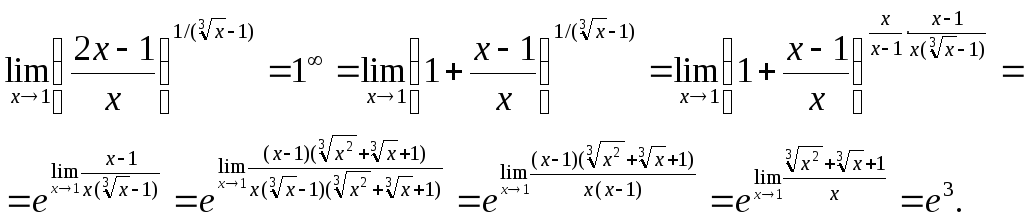
Пример 14. Вычислить пределы функций.
![]()
