Решение типовых заданий
Пример 1. Найти область определения функций
а)
;
б)
;
в)
.
Решение. а) Область определения функции X найдем
из системы неравенств
откуда
или
.
б) Имеем систему
.
Решая первое неравенство,
получим
;
решая второе, найдем
,
откуда
и
.
С помощью числовой оси (рис.4) находим
решение системы неравенств:
,т.е.
область определения функции
.
Рисунок 4
в
)
Область определения найдем из неравенства
,
откуда
.
Так как при любом
,
то перейдем к равносильному неравенству
,
откуда
,
или
Очевидно, что полученные неравенства
справедливы при любом
,
т.е. область определения функции
.
Пример 2. Найти область значений функций:
Решение. Преобразуем функцию
Так как синус любого угла по абсолютной
величине не превосходит 1, т.е.
,
то
,
,
Итак, область значений функции
Пример 3. Выяснить четность (нечетность) функций:
а)
б)
в)
решение:
а)
Так как
,
то данная функция четная;
б)
(после преобразований).
Так как
,
то данная функция четная.
в)
Так как
и
,
то данная функция общего вида, т.е. ни
четная, ни нечетная.
Упражнения и задания для самостоятельной работы
Теоретические вопросы
-
Что такое функция?
-
Какие существуют способы задания функций?
-
Какую функцию называют периодической? Что такое период функции?
-
Какая функция называется четной? нечетной?
-
Какая функция называется монотонной.
Задание 1. Найти область определения функции.
Задание 2. Найти область значения функции.
Задание 3. Выяснить четность (нечетность) функции:
-
-
-
-
-
-
-
; -
-
. -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
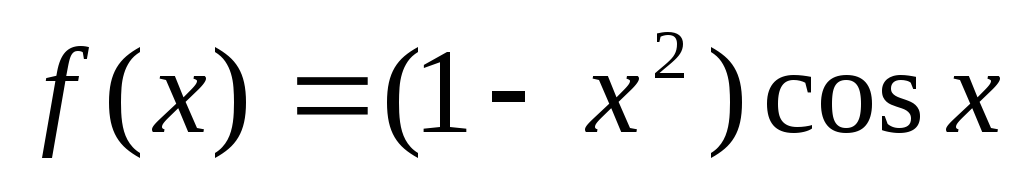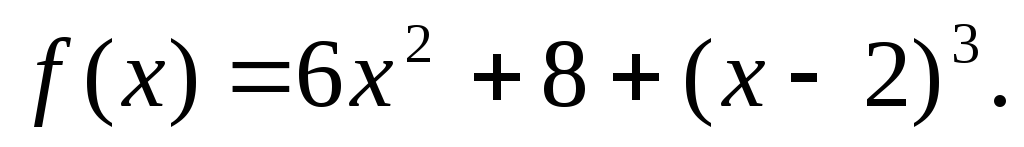
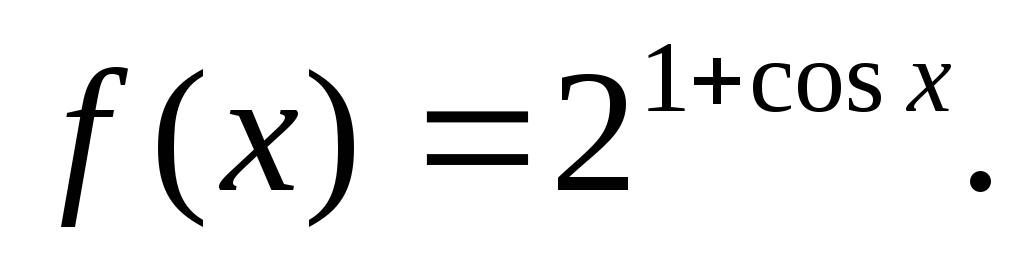
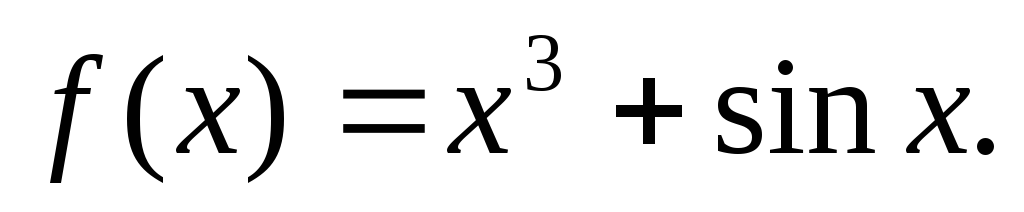
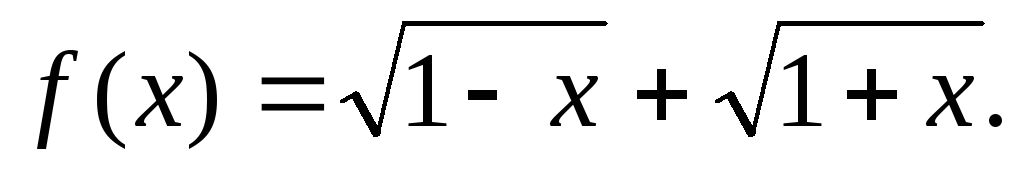
Задание 4. Построить графики функции:
-
Предел функции. Методы вычисления пределов функции.
Определение: Пусть функция
определена в некоторой проколотой
окрестности точки а. Если она
непрерывна в точке а, то назовем ее
значение в точке
пределом
функции
при стремлении х к а и будем
писать
.
Если функция
разрывна в точке
,
то может случиться, что этот разрыв
устранимый. Тогда можно изменить
значение функции в точке
или доопределить ее в этой точке так,
что в результате получится функция,
непрерывная в точке
.
Примеры:
-
Вычислить
.
Т.к. функция
непрерывна в точке
,
то предел функции при
,
равен ее значению в этой точке, т.е.
.
-
Вычислить
.
Здесь нельзя воспользоваться рассуждением
предыдущего примера, поскольку функция
не определена, а значит, разрывна в
точке
.
Выполним некоторые преобразования
аналитического выражения этой функции:
.
В проколотой окрестности точки
функция
совпадает
с функцией
,
непрерывной в этой точке и принимающей
в ней значение
.
Таким образом
.