7. Методы интегрирования

Непосредственное интегрирование

Этот метод заключается в прямом использовании табличных интегралов и свойств.

Пример.

Метод разложения

Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул.

Пример.

.

Метод подведения под знак дифференциала

Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала.

а) Подведение под знак дифференциала линейной функции

d(ах+b) = а dх, отсюда dх = d (ах + b), а 0, в частности

dх = d(х + b), dх = d(ах), т.е. дифференциал не меняется, если к переменной прибавить или отнять постоянную величину, а если переменная увеличивается в несколько раз, то дифферен­циал умножается на обратную величину.

Пример.

.

б) Подведение под знак дифференциала основных элементарных функций: e^x dx = d(e^x), cos x dx = d(sin x), x dx = d(x²)/2 и т. д.

Пример.

Метод замены переменной

Существуют две формулы замены переменной в неопреде­ленном интеграле:

1. , где x = φ(t)

2. , где φ(x) = t

Здесь x = φ(t) и t = φ(x) суть монотонные дифференцируе­мые функции своих переменных.

Искусство применения метода состоит, в основном, в выборе функций х = φ(t) или t = φ(x) так, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной.

Замечание. Подведение под знак дифференциала является частным случаем замены переменной, так как выполняются те же действия, только не вводится новая переменная. Это произ­водится в уме.

Пример.

Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x+1 = t², тогда x = t² – 1, а dx = 2t dt:

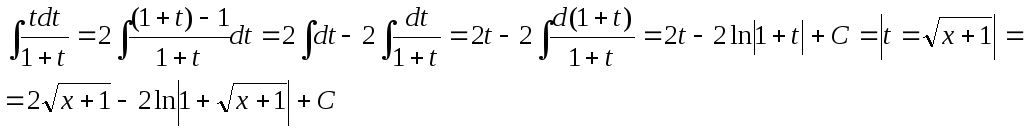
Метод интегрирования по частям

Дифференциал произведения двух функций определяется формулой

Интегрируя это равенство, получим выражение:

Отсюда . Это и есть формула интегриро­вания по частям.

Применение этого метода предполагает субъективное пред­ставление подынтегрального выражения в виде , и при этом интеграл должен быть не труднее, чем . В противном случае применение метода не имеет смысла.

Итак, искусство применения метода интегрирования по ча­стям предполагает умение выделять из подынтегральной функ­ции сомножители u и dυ с учетом вышеизложенных требований. Конечно, не все интегралы могут быть найдены этим методом.

Пример.

8. Понятие определенного интеграла, свойства

К понятию определенного интеграла приводят разнообраз­ные задачи математики, физики, химии и других точных наук, в том числе вычисление площадей плоских фигур, длин дуг, объема произведенной работы, количества вещества, образовав­шегося в результате химической реакции. Далее рассмотрим некоторые из этих задач более подробно.

Вычисление площади криволинейной трапеции

Криволинейной трапецией будем называть плоскую фигуру, ограниченную осью ОХ, графиком непрерывной функции у = f(x) и двумя вертикальными прямыми х = а и х = b (рис. 5).

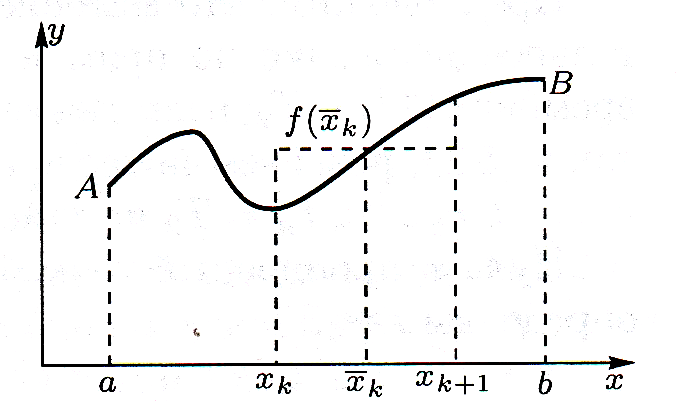
Рис. 5

Чтобы вычислить площадь криволинейной трапеции, проделаем следующие действия. Сначала разделим основание трапеции [а, b] на n частичных интерва­лов [х₀, х₁], [х₁, x₂], … , [х_n-1,х_n], считая что

a = x₀ < x₁ < x₂ < …< x_n-1 < x_n = b

Проведем через точки разбиения прямые, параллельные оси ОУ, тогда фигура аАВb разделится на n элементарных криво­линейных трапеций. Обозначим Δx_k = х_k+1 – х_k, k = 0,1, . . . , n – 1.

Вычислим площадь прямоугольника с основанием Δх_k и вы­сотой

,

что приближенно равняется площади k-й элементарной криволи­нейной трапеции с тем же основанием (см. рис. 5). Учитывая, что площадь фигуры, составленной из нескольких непересекаю­щихся фигур, равна сумме площадей этих фигур, получим

Эта сумма является приближением для искомой площади, причем чем Δх_k меньше (а следовательно, n больше), тем это приближение точнее, т. е.

S = площадь аАВb = lim S_n,

где переход к пределу совершается при условии max Δх_k —> 0.

Определенный интеграл. Теорема существования.

Рассмотренный пример, если абстрагироваться от физиче­ского смысла переменных и их обозначений, приводит к одной математической задаче: найти предел интегральной суммы

(10)

при max Δх_k —> 0, где f(x) — функция, непрерывная на промежутке [а, b]. Предел этой суммы называется определенным ин­тегралом от функции f(x) в пределах от a до b и обозначается

Функция f(x) называется подынтегральной функцией; f(x)dx — подын­тегральным выражением; x — переменной интегрирования: а — нижним, b — верхним пределами интеграла; [а, b] — промежут­ком интегрирования.

Определение. Определенным интегралом называется предел, к которому стремится интегральная сумма (10) при стремлении к нулю длины наибольшего частичного интервала Δх_k.

Теорема (существования определенного интеграла). Если функция f(x) непрерывна в замкнутом интервале [а, b], то ее n-я интегральная сумма стремится к пределу при стремлении к ну­лю наибольшего частичного интервала. Этот предел не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.

Свойства определенного интеграла

Исходя из определения можно установить следующие свойс­тва определенного интеграла.

1. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых:

2. Постоянный множитель подынтегральной функции можно выносить за символ интеграла:

3. Если верхний и нижний пределы интеграла поменять ме­стами, то интеграл изменит знак:

, в частности

4. Если интервал интегрирования [а, b] разбить на две части [а, с] и [с, b], то

(свойство аддитивности определенного интеграла).

5. Если подынтегральная функция в интервале интегрирова­ния не меняет знака, то интеграл представляет собой число того же знака, что и функция. В частности, если в интервале [а, b], где а < b, то

.

Формула Ньютона-Лейбница

Непосредственное вычисление интеграла как предела соот­ветствующих интегральных сумм затруднительно, да и не требуется, поскольку для этой цели можно воспользоваться следующей теоремой.

Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла:

, где F`(x) = f(x) (11)

Равенство (11) называется формулой Ньютона-Лейбница.

Разность значений функции часто записывают так:

(12)

В случае использования (12) формуле можно придать вид

, где F`(x) = f(x)

Формула Ньютона-Лейбница дает нам альтернативный способ вычисления определенных интегралов. Она позволяет находить их по формуле