4.3.3 Электрическая схема установки

В данной лабораторной работе объектом исследования является нить лампы накаливания Л , включенной в цепь постоянного тока.

Схема включения приведена на рисунке 4.3

Рисунок 4.3 Блок – схема включения лампы накаливания

Лампа накаливания Л включена в цепь выпрямителя В , на вход которого подается переменное напряжение с лабораторного автотрансформатора – ЛАТРа, включенного в сеть ~220 В. Ток, протекающий через лампу, измеряется амперметром А , напряжение – вольтметром V.

Подавая с ЛАТРа различное напряжение на вход выпрямителя В, можно добиться различного свечения лампы. Энергия, потребляемая лампой за единицу времени, равна произведению тока I, протекающего через лампу, на напряжение U на лампе.

4.4 Порядок выполнения работы

1. Включить ЛАТР в сеть и постепенно увеличивать напряжение до начала свечения нити исследуемой лампы – объекта исследования.

2. Навести пирометр на излучающую поверхность исследуемой лампы.

3. Если поверхность видна не отчетливо, то перемещая объектив пирометра, добиться резкого изображения объекта исследования

Данный пункт выполняется только лаборантом или

преподавателем.

4. Включить источник ИП накала нити лампочки пирометра. Если нить пирометра видна не отчетливо, то, передвигая окуляр, добиться ее резкого изображения.

5. С помощью реостата R (поворотное кольцо с нулевой отметкой) подобрать такой накал нити пирометра, чтобы ее верхняя часть «исчезла» на фоне изображения исследуемого объекта.

6. Записать показания пирометра -T_я , а также показания амперметра I и вольтметра U , включенных в цепь исследуемого объекта – лампы накаливания.

7. По формуле (36) найти истинную температуру T_T нити исследуемой лампы, считать для вольфрама (для λ = 0,66 мкм).

8. Измерения, отмеченные в пунктах 5 и 6, повторить при трех различных температурах накала нити исследуемой лампы.

9. По формуле (32) вычислить суммарный коэффициент поглощения для каждой температуры.

10. Вычислить абсолютную и относительную погрешности.

11. Результаты измерений и расчетов занести в таблицу 4.1.

Таблица 4.1

№ п/п	I A	U B	Tя 0C	Tя 0К	ΔTя 0К	TT 0К	ΔTT 0К	aT	ΔaT
1 2 3 4

12. Отключить установку питания объекта исследования и пирометра. Отчет по данной работе, кроме результатов измерений, должен содержать принципиальную схему устройства оптического пирометра и схему включения объекта исследований – лампы накаливания.

4.5 Техника безопасности

1. Включение установки производится только через ЛАТР с помощью тумблера «Вкл.”.

2. Запрещается касаться токоведущих частей схемы при включении в сеть ЛАТРа.

3. По окончании работы снять напряжение с ЛАТРа, а потом отключить установку.

4.6 Вопросы для самоподготовки

1. Характеристики теплового излучения.

2. Законы теплового излучения.

3. Каково устройство оптического пирометра?

4. Что такое яркостная температура?

5. Как определить опытным путем суммарный коэффициент поглощения?

6. Вывести рабочую формулу для истинной температуры и суммарного коэффициента поглощения.

5 Лабораторная работа №4.10. ИССЛЕДОВАНИЕ СПЕКТРА АТОМАРНОГО ВОДОРОДА И ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА

Цель работы: Изучение видимой части спектра излучения атомов и определение постоянной Ридберга.

5.1 Теоретические сведения

Спектр излучения является важной характеристикой вещества, которое позволяет установить некоторые особенности его строения, свойства атомов и молекул. Спектры испускания и поглощения разных химических элементов состоят из множества линий, группы которых называются спектральными сериями. Наиболее простой спектр имеет атом водорода. Длины волн излучения описываются формулой Бальмера-Ритца:

, (5.1)

где λ – длина волны излучения,

R – постоянная Ридберга,

n₁ и n₂ – целые числа, соответствующие номеру стационарного состояния атома.

Каждой серии спектра атома водорода соответствует определенное значение n₁ . n₂ может принимать значения от n₁ +1 до +∞.

Таким образом спектр излучения водорода можно представить в виде следующих серий (рисунок 5.1).

Серия Лаймана (n₁ =1) – ультрафиолетовая область спектра.

Серия Бальмера ((n₁ =2) – видимая область спектра и ближняя часть ультрафиолетовой области.

Серия Пашена (n₁ =3) – инфракрасная область спектра.

Серия Брэкета (n₁ =4) - инфракрасная область спектра.

Серия Пфундта (n₁ =5) - инфракрасная область спектра.

Рисунок 5.1

Линия, соответствующая переходу электрона в атоме водорода с уровня n=3 на уровень n=2 в серии Бальмера является наиболее яркой и называется головной линией (первая линия каждой серии – головная).

В данной работе определяются длины волн четырех линий серии Бальмера, принадлежащих видимой области спектра. Эти линии имеют следующие обозначения:

H_α – красная линия (n₂ =3),

H_β –голубая линия (n₂ =4),

H_γ – сине-голубая (n₂ =5),

H_δ – фиолетовая (n₂ =6).

Как известно, экспериментальные исследования спектров излучения атомов послужили основой для построения теории, объясняющей их строение и закономерности в спектрах излучения и поглощения. Попытки построить модель атома, которая смогла бы объяснить возникновение спектров испускания, были предприняты Томсоном (1903 г.), Резерфордом (1913 г.) и потерпели неудачу.

Первая попытка построения неклассической теории атома была предпринята Н.Бором в 1913 г. В основе этой теории лежала идея связать в единое целое эмпирические закономерности линейчатых спектров (формулу Бальмера), ядерную модель Резерфорда и квантовый характер излучения света (теория Планка). В теории Бора не содержалось принципиального отказа от описания поведения электрона в атоме при помощи законов классической физики. Однако Бору пришлось дополнить классическое описание состояния электрона в атоме некоторыми ограничениями. Эти ограничения были сформулированы в виде постулатов.

Первый постулат Бора (постулат стационарных состояний) заключается в следующем: из бесконечного множества электронных орбит, возможных с точки зрения классической механики, осуществляются только некоторые дискретные орбиты, удовлетворяющие определенным квантовым состояниям, энергии которых составляют дискретный ряд: W₁ ,W₂,W₃,...W_n. В стационарном состоянии атом не излучает.

Второй постулат Бора (правила квантования орбит): в стационарном состоянии атома электрон движется только по таким орбитам, для которых момент импульса электрона удовлетворяет условию:

, (5.2)

где ħ – постоянная Планка, равная 1,054^.10^-34 Дж^.с;

n=1,2,3,…; m_e – масса электрона;

r_n – радиус соответствующей орбиты.;

v_n – скорость электрона.

Третий постулат Бора (правило частот): при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии.

Излучение происходит при переходе из состояния с большей энергией в состояние с меньшей энергией, т.е. при переходе электрона с орбиты, более удаленной от ядра, на более ближнюю к ядру:

(5.3)

где  – энергия электрона на соответствующей орбите;

 – квант энергии;

 – циклическая частота излучения.

Теория Бора дала возможность построить модель атома водорода и водородоподобных ионов . Согласно этой теории атом состоит из ядра и электрона, движущегося по круговым стационарным орбитам. Электрон удерживается на круговой орбите кулоновской силой. Определим полную энергию электрона в водородоподобном атоме. Полная энергия электрона на орбите складывается из кинетической энергии электрона 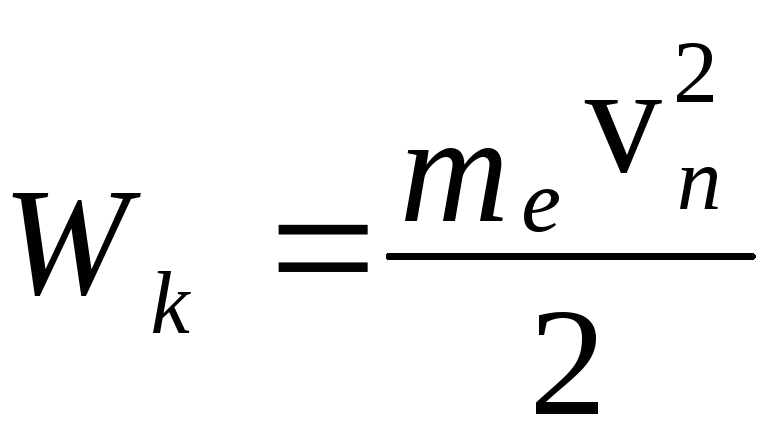и потенциальной энергии взаимодействия электрона с ядром ,

где  – масса электрона;

 – линейная скорость электрона на орбите;

 – зарядовое число ядра атома;

 – заряд электрона;

 – электрическая постоянная;

 – радиус орбиты.

. (5.4)

Кулоновская сила сообщает электрону центростремительное ускорение, т.е.

. (5.5)

Из (5.5) следует, что

, (5.6)

т.е. потенциальная энергия равна удвоенному значению его кинетической энергии:

. (5.7)

Подставив (5.5) в (5.4), получим:

. (5.8)

Для определения радиуса орбиты воспользуемся вторым постулатом Бора и равенством (5.5). Решив систему двух уравнений относительно , получим:

. (5.9)

Таким образом r_n n², т.е. с ростом номера орбиты радиус ее растет. Для водорода (z=1) при n=1: радиус первой боровской орбиты.

Подставив (5.9) в выражение (5.8), получим:

(5.10)

Таким образом, из выражения (5.10) следует:

• Полная энергия электрона в атоме отрицательна.

• Энергия электрона в атоме принимает дискретный ряд значений, которые представлены на рисунке 5.1

При n=1 энергия минимальна, при n→∞ энергия электрона максимальна, и он покидает атом. Атом при этом ионизируется.

Воспользуемся третьим постулатом Бора и формулой энергии электрона (5.10), определим длину волны излучения при переходе электрона из одного энергетического состояния в другое.

Длина волны связана с циклической частотой соотношением , где с – скорость света в вакууме. Поскольку то , где  – энергия на n уровне;  – энергия на m уровне. Причем n > m.

. (5.11)

Для длины волны формулу (5.11) можно записать в виде:

. (5.12)

Обозначив 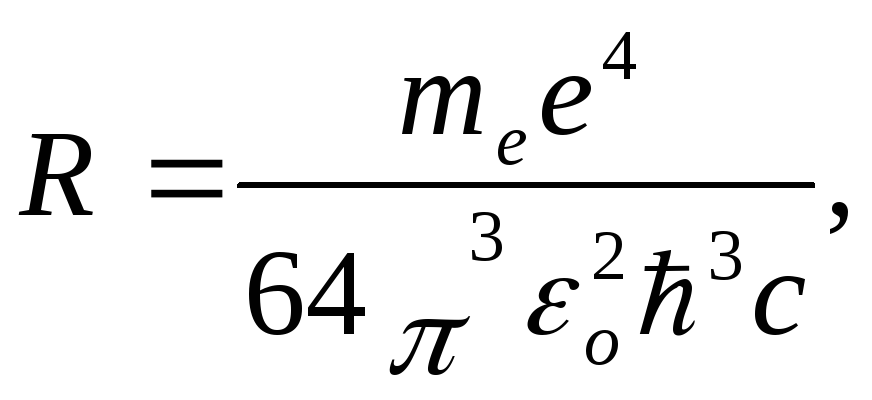получим обобщенную формулу Бальмера:

(5.13)

где R – постоянная Ридберга.

Теория Бора смогла объяснить факт испускания света атомом: при переходе электрона из состояния с большей энергией W_n в состояние с меньшей энергией W_m атом излучает квант энергии .(На рисунке 5.2 – переходы 2 и 3).

При поглощении порции энергии ΔW электрон переходит из основного состояния (n=1) в возбужденное (переход 1 на рисунке 5.2). В этом состоянии атом пребывает незначительный промежуток времени Δt^ с, а затем переходит в основное состояние, причем этот переход может осуществляться ступенчато.

Рисунок 5.2 - Возможные переходы электронов в атоме.