Лабораторная работа № 1

Синтез сигналов по фурье

Цель работы — изучение возможности аппроксимаций сигналов многочленом Фурье по ортогональной системе тригонометрических функций.

Теоретические сведения

1. Ряды Фурье и тригонометрические полиномы.

Для теории сигналов и их обработки важное значение имеет разложение заданной функции по различным ортогональным системам функций . Напомним основные определения, относящиеся к свойствам ортогональных систем.

Бесконечная система действительных функций

(2.1) называется ортогональной на отрезке , если

при . (2.2)

При этом предполагается, что

, (2.3)

т. е. что никакая из функций рассматриваемой системы (2.1) не равна тождественно нулю.

Условие (2.2) выражает попарную ортогональность функций системы (2.1). Величина

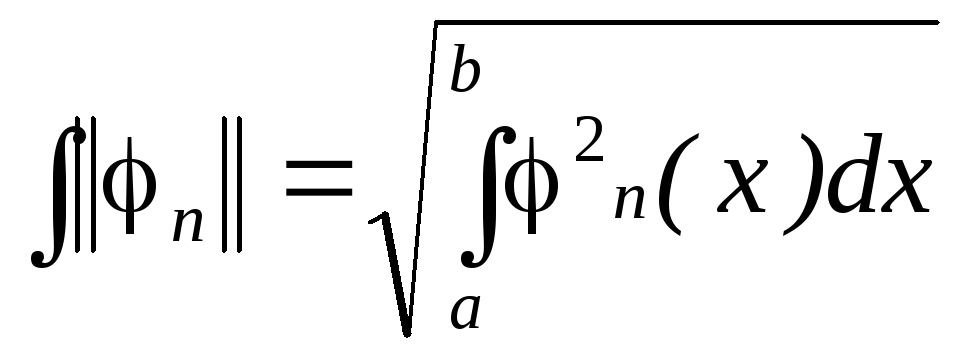называется нормой функций . (2.4)

Функция для которой выполняется условие

(2.5)

называется нормированной функцией, а система нормированных функций в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой.. В математике доказывается, что если функции непрерывны, то 'произвольная кусочно-непрерывная функция , для которой выполняется условие

может быть представлена в виде суммы ряда

(2.6)

Интеграл в предыдущем выражении вычисляется по области определения .

Умножим обе части уравнения (2.6) на и проинтегрируем в пределах . Все слагаемые вида при обращаются

в нуль в силу ортогональности функций и . В правой части оста- ется одно слагаемое

,

что позволяет написать

,

откуда следует важное соотношение

(2.7)

Ряд (2.6), в котором коэффициенты определены по формуле (2.7), называется обобщенным рядом Фурье по данной системе . Совокупность коэффициентов называется спектром сигнала в ортогональной системе и полностью определяет этот сигнал.

Обобщенный ряд Фурье обладает следующим важным свойством: при заданной системе функций и фиксированном числе слагаемых ряда (2.6) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции . Это означает, что среднеквадратическая ошибка, под которой подразумевается величина

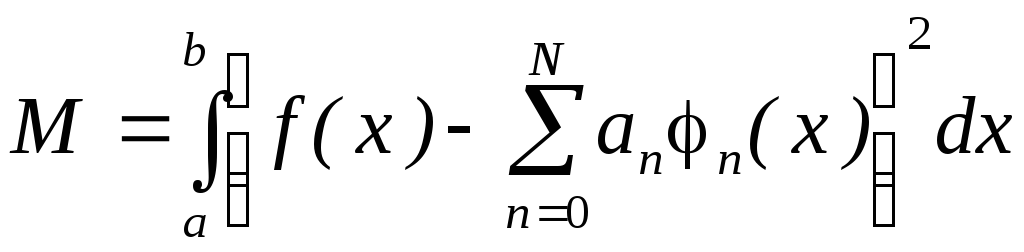
достигает минимума, когда коэффициенты ряда .

Действительно, подставив в предыдущее выражение и использовав равенства (2.2), (2.4) и (2.7), получим

Отсюда следует, что достигает минимума при , т. е. при Таким образом,

.

Так как величина

является квадратом нормы функции , а , то на основании (2.8) можно написать следующее неравенство:

Это основное неравенство, называемое неравенством Бесселя, справедливо для любой ортогональной системы.

Ортогональная система называется полной, если увеличением числа членов в ряде среднеквадратическую ошибку М можно сделать сколь урод- но малой.

Условие полноты можно записать в виде соотношения

. (2.10)

При выполнении этого условия можно считать, что ряд (2.6) сходится в среднем, т. е.

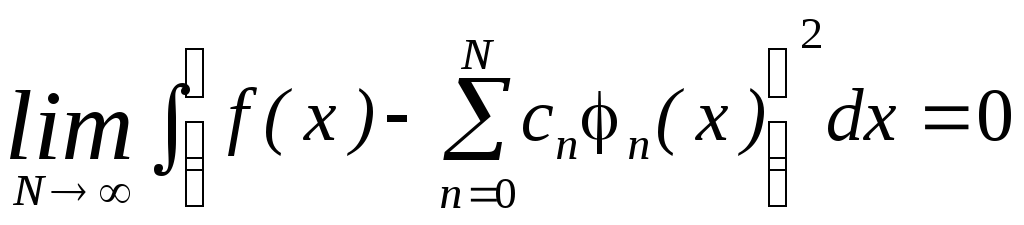. (2.11)

Из этого, однако, еще не следует, что сходится к , т.е. что

при любых значениях .

В отдельных точках на оси ряд может отличаться от хотя равенство (2.11) имеет место.

Для системы функций , принимающих комплексные значения, приведенные выше определения обобщаются следующим образом:

условие ортогональности

при (2.2*)

квадрат нормы функции

; (2.4*)

коэффициенты Фурье (2.7*)

.

В этих выражениях обозначает функцию, комплексно-сопряженную функции .

Применительно к сигналам , являющимся функциями времени, выражение (2.6) в дальнейшем будет записываться в форме

. (2.12)

В новых обозначениях квадрат нормы функции по аналогии с (2.4) будет

, (2.13)

где – энергия сигнала.

Таким образом, в соответствии с формулой (2.10) энергия сигнала , (2.14)

а при использовании ортонормированной системы функций

. (2.14*)

При этом имеется в виду, что промежуток времени в котором определяется энергия Э, является интервалом ортогональности для системы функций .

Очевидно, что средняя за время мощность сигнала

. (2.15)

Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди разнообразных задач, требующих разложения сложного сигнала, наиболее важными являются: 1) точное разложение на простейшие ортогональные функции; 2) аппроксимация сигналов, процессов или характеристик, когда требуется свести к минимуму число членов ряда (при заданной допусти- мой погрешности).

При первой постановке задачи наибольшее распространение получила ортогональная система основных тригонометрических функций — синусов и косинусов. Это объясняется рядом причин. Во-первых, гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении через любую линейную цепь (с постоянными параметрами). Изменяются лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи. По этим, а также и некоторым другим причинам гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

При второй постановке задачи — приближенном разложении функций — применяются разнообразные ортогональные системы функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра, функции Уолша и многие другие. При разложении периодического сигнала в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут

или

Интервал ортогональности в обоих случаях совпадает с периодом функции .

Система функций (2.18) приводит к тригонометрической форме ряда Фурье, а система (2.19) — к комплексной форме. Между этими двумя формами существует простая связь.

Воспользуемся сначала ортогональной системой (2.17). Тогда ряд Фурье должен быть записан в форме

(2.20)

Совокупность коэффициентов ряда Фурье в базисе тригонометрических функций называется частотным спектром периодического сигнала. Коэффициенты ряда (2.20) легко определяются с помощью формул, приведенных ранее.

Из формулы (2.6*) следует, что

(2.21)

Таким образом, независимо от n норма . Используя формулу (2.9*), получаем

(2.22)

В выражениях (2.21) и (2.22) учтено, что функции соответствует комплексно-сопряженная функция .

Коэффициенты в общем случае являются комплексными величинами. Подставив в (2.22) , получим

. (2.23)

Косинусная (действительная) и синусная (мнимая) части коэффициента определяются формулами

, . (2.24)

Коэффициенты часто бывает удобно записывать в форме

,

где , .

Модуль является функцией, четной относительно , а аргумент — нечетной (последнее вытекает непосредственно из выражений (2.24), показывающих, что является четной, а нечетной функциями ).

Общее выражение (2.20) можно привести к виду

(2.28)

Теперь нетрудно перейти к тригонометрической форме ряда Фурье. Выделив из ряда (2.28) пару слагаемых, соответствующую какому-либо за- данному значению , например , и, учтя соотношения, , получим для суммы этих слагаемых

.

Отсюда видно, что при переходе к тригонометрической форме ряд (2.28) необходимо записать следующим образом:

(2.30)

Смысл удвоения коэффициентов Фурье в тригонометрическом ряду при становится ясным из рассмотрения векторной диаграммы соответствующей (2.29) при =2. Вещественная функция получается как сумма проекций на горизонтальную ось 0В двух векторов длиной , вращающихся с угловой частотой во взаимно противоположных направлениях. Вектор, вращающийся против часовой стрелки, соответствует положительной частоте, а вектор, вращающийся по часовой стрелке, — отрицательной. После перехода к тригонометрической форме понятие «.отрицательная частота» теряет смысл. Коэффициент не удваивается, так как в спектре периодического сигнала составляющая с нулевой частотой не имеет «дублера».

Вместо выражения (2.30) в математической и радиотехнической литера- туре часто встречается следующая форма записи:

(2.31)

причем .

Из сопоставления выражений (2.31) и (2.30) видно, что амплитуда n-й гармоники связана с коэффициентом ряда (2.28) соотношением

, а .

Таким образом, для всех положительных значений n (включая и )

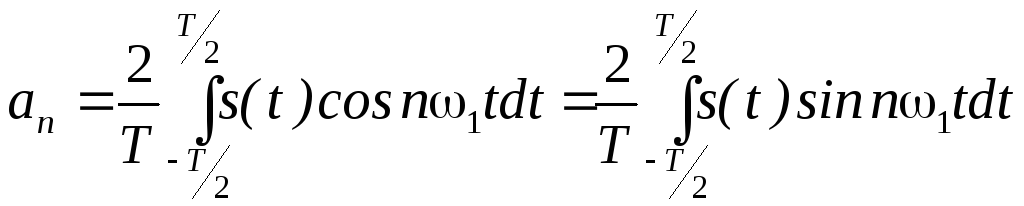(2.32)

Если сигнал представляет собой функцию, четную относительно , т. е. , в тригонометрической записи ряда остаются только косинусоидальные члены, так как коэффициенты в соответствии с формулой (2.32) обращаются в нуль. Для нечетной относительно функции наоборот, в нуль обращаются коэффициенты и ряд состоит только из синусоидальных членов.

Две характеристики — амплитудная и фазовая, т. е. модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектрa периодического колебания. Наглядное представление о «ширине» спектра дает графическое изображение спектра амплитуд. Для исчерпывающей характеристики спектра подобные построения должны быть дополнены заданием начальных фаз отдельных гармоник.

Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, соответствующих дискретным частотам и т. д.

Использование для гармонического анализа сложных периодических колебаний рядов Фурье в сочетании с принципом наложения представляет собой эффективное средство для изучения влияния линейных цепей на про- хождение сигналов. Следует, правда, отметить, что определение сигнала на выходе цепи по сумме гармоник с заданными амплитудами и фазами является непростой задачей, особенно если не обеспечивается быстрая сходимость ряда Фурье, представляющего входной сигнал. Наиболее распространенные в радиотехнике сигналы не соответствуют этому условию, и для удовлетворительного воспроизведения формы сигналов обычно необходимо суммировать большое число гармоник.