1. Аффинные преобразования на плоскости
Аффинное отображение - такое отображение плоскости (пространства) на другую плоскость (пространство), при котором каждая прямая отображается в прямую (рис.1). Аффинное преобразование есть аффинное отображение плоскости на себя.
Математический аппарат аффинных преобразований лежит в основе построения изображений в компьютерной графике.
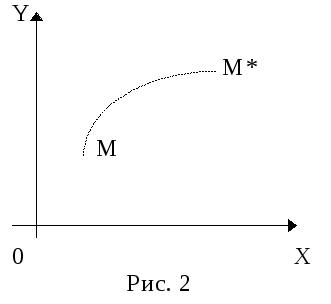
Преобразование, которое переводит точку М (x,y) в другую точку М*(x*,y*), (рис.2), задается формулами
x* = x + y + (11)
y* = x + y +
где , , , , , - произвольные числа, связанные неравенством:
0
В аффинных преобразованиях на плоскости особую роль играют несколько важных частных случаев, имеющих четкую геометрическую интерпретацию, а именно:
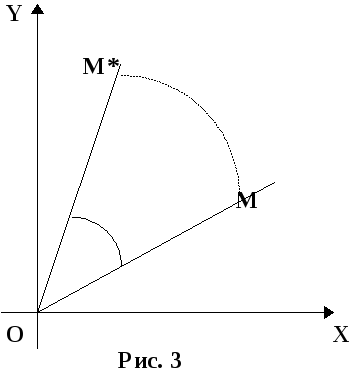
а). Поворот вокруг начальной точки на угол (рис. 3).
x* = x cos - y sin (21)
y* = x sin + y cos
x* = x (31)
y* = y
Для растяжения: 1; 1; для сжатия: 1 0; 1 0.
в). Отражение относительно оси абсцисс (рис. 5).
x* = x (41)
y* = - y
г). Перенос (рис. 6).
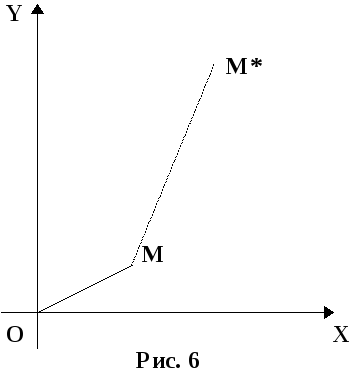
y* = y +
где , - координаты вектора переноса М М*.
2. Однородные координаты точки
Однородными координатами точки М(x,y) называется любая тройка одновременно не равных нулю чисел x1, x2, x3, связанных с заданными координатами (x,y) следующими соотношениями:
x1/x3 = x; x2/x3 =y; ( 61 )
То есть, в общем случае однородные координаты точки можно представить тройкой (hx, hy, h). При решении задач компьютерной графики обычно используется частный случай, а именно: произвольной точке М (x,y) на плоскости ставится в соответствие точка М*(x,y,1) в пространстве (рис. 7).
При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.
Аффинные преобразования в пространстве
Аналогично тому, как это было сделано для двумерного случая, заменим координатную тройку (x, у, z), задающую точку в пространстве, на четверку (x, у, z, 1) или в общем виде на (hx, hy, hz, 1), где h 0.
Можно показать, что любое аффинное преобразование в трехмерном пространстве может быть представлено в виде комбинации поворотов, растяжений (сжатий), отражений и переносов. Выпишем все матрицы, определяющие эти преобразования:
А. Матрицы поворота в пространстве
Матрица поворота вокруг оси абцисс на угол :
1 0 0 0
Rx = 0 cos sin 0 (1)
0 - sin cos 0
0 0 0 1
Матрица поворота вокруг оси ординат на угол :
cos 0 - sin 0
Ry = 0 1 0 0 (2)
sin 0 cos 0
0 0 0 1
Матрица поворота вокруг оси аппликат на угол :
cos sin 0 0
Rz = - sin cos 0 0 (3)
0 0 1 0
0 0 0 1
Б. Матрица растяжения (сжатия)
0 0 0
D = 0 0 0 (4)
0 0 0
0 0 0 1
где , , - коэффициенты растяжения (сжатия) вдоль осей абсцисс, ординат и аппликат, соответственно.
В. Матрицы отражения:
Матрица отражения относительно плоскости XY:
1 0 0 0
Мz = 0 1 0 0 (5)
0 0 - 1 0
0 0 0 1
Матрица отражения относительно плоскости YZ:
- 1 0 0 0
Мx = 0 1 0 0 (6)
0 0 1 0
0 0 0 1
Матрица отражения относительно плоскости ZX:
1 0 0 0
Мy = 0 - 1 0 0 (7)
0 0 1 0
0 0 0 1
Г. Матрица переноса
1 0 0 0
T = 0 1 0 0 (8)
0 0 1 0
1
где ( , , ) - вектор переноса.
Матрицы (18) отражают простейшие геометрические преобразования точки в пространстве. Матрица сложного аффинного преобразования получается в результате перемножения такого рода матриц и имеет в общем случае вид:
1 2 3 0
P = 1 2 3 0 (9)
1 2 3 0
1
При помощи указанных матриц можно преобразовывать любые пространственные тела, заданные множеством вершин, соединенных отрезками прямых.
Пусть требуется подвергнуть заданному аффинному преобразованию выпуклый многогранник, имеющий n вершин (рис. 1). Матрица, однозначно описывающая такое тело, имеет вид:
x1 y1 z1 1
x2 y2 z2 1
V0 = . . . . (10)
. . . .
xn yn zn 1
где xi , yi , zi - координаты i - й вершины.
По геометрическому описанию преобразования находим его матрицу P . Тогда новый выпуклый многогранник описывается набором вершин:
x1*
y1*
z1*
1
x2* y2* z2* 1
V* = V0 P = . . . . (11)
. . . .
xn* yn* zn* 1