laby po fizike / Laboratornaia rabota №29

7

Московский Энергетический Институт

(технический университет)

Кафедра ОФ и ЯС

Лаборатория электричества и магнетизма.

Лабораторная работа №29

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ

Группа:
Студент:
Преподаватель:
К работе допущен:
Дата выполнения:
Работу сделал:
Работу сдал:

МОСКВА 2004

Цель работы - ознакомление с характером затухающих колеба­ний; определение основных характеристик колебательного контура.

1. Теоретические основы работы

Колебательным контуром называется электрическая цепь, содер­жащая катушку с индуктивностью L, конденсатор с емкостью С, и резистор с сопротивлением R (рис. 1). Если зарядить конденсатор от батареи if до напряжения U_m, а затем с помощью переключателя К замкнуть на колебательный контур, то конденсатор начнет разряжаться и в контуре возникнут электромагнитные колебания.

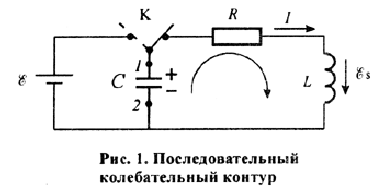
Согласно закону Ома для участка цепи

, (1)

где

, (конденсатор разряжается);

;

.

Отсюда следует:

.

Последнее уравнение можно записать в виде

. (2)

Принято обозначать:

- циклическая частота собственных колебаний;

- коэффициент затухания.

С учетом введенных обозначений дифференциальное уравнение (2) запишем в виде

. (3)

Уравнение (3) представляет собой дифференциальное уравнение затухающих электрических колебаний. Его решение имеет вид:

,

или

,

где - амплитуда колебаний заряда; - цик­лическая частота затухающих колебаний; - начальная фаза колебани­й. Учитывая, что U=qС, для напряжения на конденсаторе получаем

, (4)

или

,

где - амплитуда колебаний напряжения на конденсаторе.

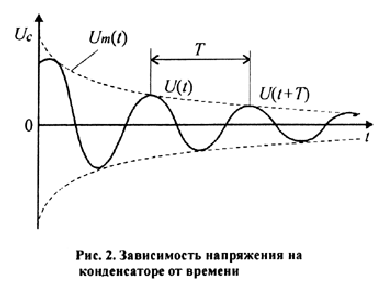
Коэффициент затухания характеризует скорость убывания ампли­туды колебаний (за время амплитуда колебаний уменьшается в е раз). На рис. 2 показана зависимость напряжения на конденсаторе от времени.

Период колебаний определяется по формуле

. (5)

Логарифмическим декрементом колебаний называется логарифм отношения амплитуд напряжения, разделенных периодом колебаний:

. (6)

Поскольку , a ,

то логарифмический декремент

(7)

2. Описание экспериментальной установки

Принципиальная схема установки приведена на рис. 3.

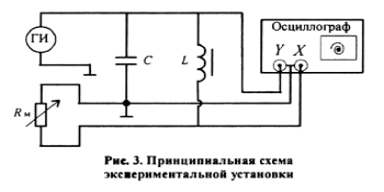
Колебательный контур содержит конденсатор емкостью С, катуш­ку индуктивностью L и магазин сопротивлений R_M. Периодическая зарядка конденсатора осуществляется прямоугольными импульсами от генератора импульсов (ГИ). Может также использоваться генератор синусоидальных сигналов с преобразователем импульсов. Напряжение U_c с конденсатора подается на вход вертикального усилителя осцилло­графа, что позволяет наблюдать затухающие колебания напряжения на экране осциллографа.

Изменяя сопротивление R_M магазина сопротивлений и проводя со­ответствующие измерения на экране осциллографа, можно определить зависимость периода Т затухающих колебаний и логарифмического декремента δ от электрического сопротивления контура.

Логарифмический декремент зависит от полного сопротивления контура:

, (8)

где .

В условиях эксперимента , поэтому период колебаний Т можно считать постоянным и равным

. (9)

Учитывая, что полное сопротивление контура R = R_м + R_к, где R_м -сопротивление магазина; R_K - сопротивление катушки, из (8) получим

.

Зависимость логарифмического декремента от сопротивления мага­зина является линейной и описывается уравнением прямой

где ; .

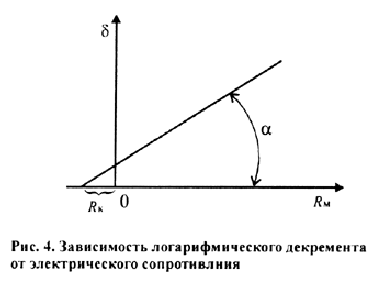
График зависимости приведен на рис. 4.

По графику можно определить сопротивление катушки, аппрокси­мируя опытную зависимость до пересечения с осью абсцисс, а индуктивность катушки рассчитать по тангенсу угла наклона прямой

. (10)

Электроемкость конденсатора С можно определить по формуле (9), зная период колебаний Т и индуктивность L катушки.

В ряде случаев удобно изучать колебательный процесс в системе координат (U_c,, I), называемой фазовой плоскостью. Кривая зависимо­сти напряжения на конденсаторе от силы тока в контуре на фазовой плоскости называется фазовой кривой.

П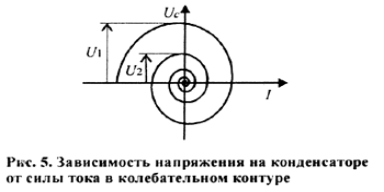ри затухающих коле­баниях амплитуды напря­жения на конденсаторе и силы тока в контуре моно­тонно убывают, и фазовая кривая имеет вид, приве­денный на рис. 5.

Фазовая кривая наблю­дается на экране осциллографа при подаче на вертикальные отклоняющие пластины напряжения с конденсатора, а на горизонтальные пластины - напряжения с магази­на сопротивлений. По фазовой кривой можно определить логарифмический декремент.

3. Данные.

Спецификация измерительных приборов

Название прибора и его тип	Предел измерения	Цена деления	Инструментальная погрешность

Зависимость логарифмического декремента от электрического сопротивления.

№	RM, Ом	n, B	U(t), B	U(t+nT), B	δ