Тема 1. Трансцендентное исчисление. А) Логарифмы.

№1. Вычислить: а) log ₁₂ 3 + log ₁₂ 4; б) log45 – log3; в) log ₆₄ 128; г) 100; д) 49; е) ; ж) .

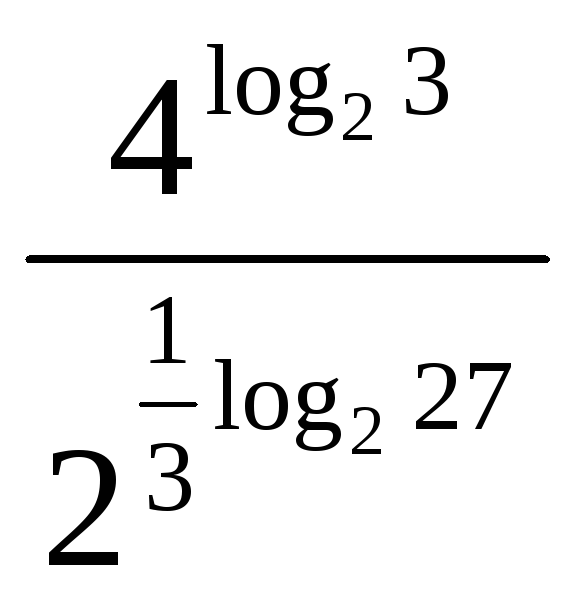№2. Вычислить log ₅ 9,8, если lg 2 = a, lg 7 = b.

№3. Доказать неравенство: log ₄ 6 > log ₆ 4.

№4. Определить знаки чисел: а) log _1,7 ; б) log _0,3.

№5. Найти область определения функции у = lg. б) Тригонометрические преобразования. №6. Найти наибольшее и наименьшее значения выражения 2 – sin . №7. Дано: cos = - , π < < . Найти остальные функции числа . №8. Упростить: а) ; б) sin ⁴ + cos ⁴ + sin ² cos ²; в) ; г) tg (π - ) + sin (2π - ) cos - cos ²(π - ); д) cos 20⁰ – sin 20⁰10⁰.

№9. Выразить через tg выражение sin ⁴ - cos ⁴. №10. Дано: tg + ctg = 3. Найти tg ³ + ctg³ . №11. Дано: ctg 2 = , 0 < < . Найти cos ². №12. Дано: cos (3π - 4) = . Найти 27 cos ⁴ 2. №13. Дано: sin = . Найти 4 tg ^2. №14. Дано: sin = . Найти 16 sin ^4. №15. Дано: ctg = 3. Найти sin . №16. Дано: cos 2 = . Найти 9.

№17. Дано: = 2arcctg (- 2) - . Найти sin 3. №18. Вычислить tg (arcsin (- 0,8)). №19. Построить на единичной окружности arccos . №20. Что больше: arccos или arcctg ?

Тема 2. Комплексные числа: №№ 4.1, 4.4, 4.5, 4.7, 4.9, 4.13 (а, в, д) [2].

Тема 3. Функции и их графики. а) Свойства функций: №№ 10.14, 10.17, 10.20, 10.24, 10.27, 10.30, 10.31, 10.36, 10.41, 10.42, 10.48, 10.51, 10.52, 10.55 [2]; б) Преобразование графиков: №№ 10.58, 10.68, 10.75, 10.81, 10.84 [2].

Тема 4. Кривые 2-го порядка. а) Задачи на построение кривых: №№ 3.28 (а), 3.2, 3.38 (а), 3.23 (а) [2]. б) Задачи на составление уравнений: №№ 3.6, 3.7, 3.13, 3.19, 3.27, 3.32, 3.40 [2]. Тема 5. Пределы. а) Определения пределов. №1. Доказать, что . Определить, начиная с какого номера члены данной последовательности будут отличаться от её предела на величину, меньшую 0,1; 0,01; 0,001. №2. Доказать, что = - 1. Определить, на какую величину должен отличаться аргумент х от - 1, чтобы данная функция отличалась от своего предела на величину, меньшую чем 0,1; 0,02.

№3. Доказать, что не существует. б) Алгебраические приёмы раскрытия неопределённостей. №4. Вычислить: а) ; б) ; в) . №№ 11.2, 11.9, 11.1, 11.5, 11.32 (а, б), 11.34 [2]. №5. Вычислить: а) ; б) . в) Замечательные пределы: №№ 11.19(а), 11.20, 11.21 (а), 11.22 (б), 11.23 (а), 11.25 (б), 11.28 (а), 11.26 (а) [2]. г) Вычисление пределов с помощью эквивалентностей. №6. Вычислить: . Тема 6. Непрерывность функции: №№ 11.54, 11.58 (а, в) [2]. №1. Исследовать на непрерывность функции: а) у = ; б) у = . Тема 7. Производная функции. а) Вычисление производных с помощью определения: №№ 12.4, 12.6, 12.10 [2]. б) Практикум по вычислению производных: №№ 12.14, 12.18, 12.17, 12.34, 12.35, 12.36, 12.38, 12.45, 12.40, 12.47, 12.70 [2]. в) Производная неявной функции: № 12.138 [2]. г) Производные высших порядков: №№ 12.76, 12.87, 12.89 [2]. Тема 8. Дифференциал: №№ 12.115, 12.116, 12.130 [2]. Тема 9. Вычисление пределов с помощью производной: №№ 12.175, 12.168, 12.169, 12.170, 12.188, 12.189, 12.171, 12.193, 12.194 [2]. Тема 10. Исследование функций. а) Исследование по отдельным факторам: №№ 12.254, 12.205, 12.217, 12.245 [2]. б) Полное исследование: №№ 12.262, 12.263, 12.270, 12.287, 12.284 [2]. Тема 11. Задачи на наибольшее и наименьшее значения: 12.234, 12.237, 12.239, 12.244 [2]. Тема 12. Функции многих переменных. а) Область определения: №№ 13.2, 13.6 [2]. б) Частные производные: №№ 13.22, 13.39, 13.79, 13.81 [2]. в) Дифференциал: №№ 13.60, 13.73, 13.76 [2]. г) Производная по направлению: №№ 13.45, 13.49, 13.50, 13.52, 13.55 [2]. Тема 13. Экстремумы функций многих переменных: №№ 13.101, 13.107 [2]. Тема 14. Условный экстремум: №№ 13.108, 13.114 [2]. Тема 15. Неопределённый интеграл. а) Непосредственное интегрирование: №№ 14.1, 14.13, 14.10, 14.16; б) Метод замены переменной: №№ 14.18, 14.22, 14.24, 14.33, 14.36, 14.28, 14.52; в) Интегрирование по частям: №№ 14.53, 14.55, 14.57, 14.58, 14.61, 14.71, 14.54; г) Интегрирование рациональных дробей: №№ 14.87, 14.85, 14.80, 14.95, 14.94; д) Интегрирование тригонометрических выражений: №№ 14.102, 14.101, 14.121, 14.125; е) Интегрирование иррациональных выражений: №№ 14.141, 14.145, 14.146, 14.150, 14.153 [2]. Тема 16. Определённый интеграл: №№ 15.3, 15.26, 15.34 [2]. Тема 17. Несобственные интегралы: №№ 15.68, 15.69, 15.81, 15.85 [2]. Тема 18. Геометрические приложения определённого интеграла. а) Площади фигур: №№ 15.53, 15.49; б) Объёмы тел вращения: №№ 15.57, 15.64 [2]. Тема 19. Дифференциальные уравнения первого порядка. а) Уравнения с разделяющимися переменными: №№ 16.13, 16.14; б) Однородные уравнения: №№ 16.23, 16.28; в) Линейные уравнения: №№ 16.30, 16.35; г) Уравнения Бернулли: №№ 16.37, 16.40; д) Уравнения в полных дифференциалах: №№ 16.42, 16.44 [2]. Тема 20. Уравнения высших порядков, допускающие понижение порядка: №№ 16.48, 16.54, 16.55, 16.57, 16.58 [2]. Тема 21. Линейные уравнения высших порядков с постоянными коэффициентами. а) Однородные уравнения: №№ 14.61 – 16.64; б) Неоднородные уравнения: №№ 16.76, 16.82 [2]. Тема 22. Числовые ряды. а) Знакоположительные ряды: №№ 17.12, 17.14, 17.17, 17.21, 17.25, 17.27, 17.28, 17.34; б) Знакопеременные ряды: №№ 17.40, 17.42, 17.46 [2]. Тема 23. Степенные ряды: №№ 17.61, 17.64, 17.63 [2]. Тема 24. Ряды Тейлора и Маклорена. а) Разложение функций в ряд Тейлора: № 17.86; б) Разложение функций в ряды Маклорена с помощью основных разложений: №№ 17.71, 17.73, 17.74; в) Почленное интегрирование и дифференцирование рядов: №№ 17.76, 17.80; г) Приближённые вычисления с помощью рядов: №№ 17.89, 17.93, 17.96 [2].

Домашние задания:

Тема 1. №1. Вычислить: а) 16; б) lg│cos π│ + log ₄ 1.

№2. Что больше: log ₃ 4 или log _0,5 7? №3. Определить знак числа 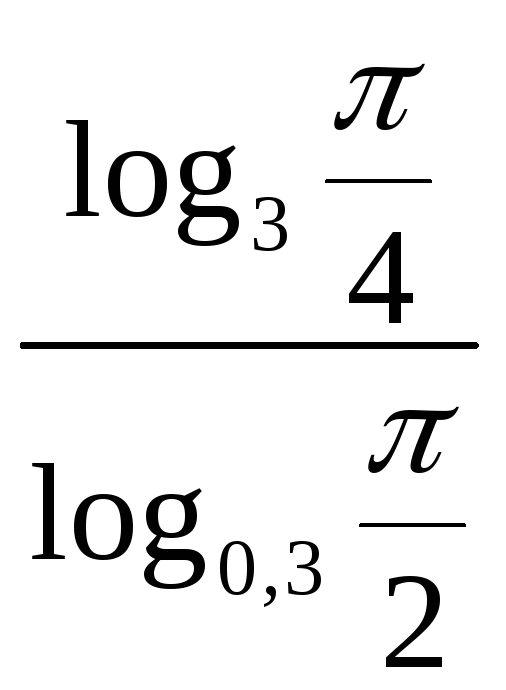. №4. Найти область определения функции у = lg . №5. Дано: ctg = - , 630⁰ < < 720⁰. Найти остальные функции этого угла. №6. Упростить: а) ; б) ; в) cos ; г) 8 cos 20⁰ cos 40⁰ cos 80⁰; д) sin. №7. Дано: tg + ctg = 3. Найти sec² + cosec².

№8. Дано: cos = , < < 2π. Найти tg 2. Тема 2: №№ 4.3, 4.6 (а, г, ж, и), 4.8, 4.10, 4.13 (б, г, е) [2]. Тема 3: №№ 10.15, 10.25, 10.29, 10.33, 10.34, 10.46, 10.50, 10.54, 10.69, 10.82 [2].

Тема 4: №№ 3.4 (в), 3.23 (б), 3.28 (б), 3.38 (б), 3.8, 3.14, 3.24, 3.29, 3.31, 3.35, 3.37 [2]. Тема 5. №1. Доказать, что . Определить, начиная с какого номера члены данной последовательности будут отличаться от её предела на величину, меньшую 0,1; 0,01; 0,001. №2. Доказать, что = - 2. Определить, на какую величину должен отличаться аргумент х от - 1, чтобы данная функция отличалась от своего предела на величину, меньшую чем 0,1; 0,03.

№3. Доказать, что не существует. №№ 11.11, 11.7, 11.6, 11.32 (в), 11.34 (б), 11.41 (б), 11.22 (а), 11.37, 11.23 (б), 11.43 (а), 11.27 (а) [2]. №4. Вычислить: . Тема 6: №№ 11.56 (а), 11.57, 11.58 (б) [2]. №1. Исследовать на непрерывность функцию у = . Тема 7: №№ 12.6, 12.12, 12.30, 12.43, 12.55, 12.63, 12.68, 12.71, 12.142, 12.91, 12.90, 12.95. Тема 8: №№ 12.126, 12.131, 12.129 [2]. Тема 9: №№ 12.174, 12.183, 12.184, 12.191, 12.195, 12.196 [2].

Тема 10: №№ 12.258, 12.213, 12.221, 12.252, 12.268, 12.265, 12.277, 12.274 [2]. Тема 11: №№ 12.236, 12.238, 12.240 [2]. Тема 12: №№ 13.5, 13.7, 13.30, 13.38, 13.86, 13.66, 13.75, 13.47, 13.53, 13.56 [2]. Тема 13: №№ 13.103, 13.106 [2]. Тема 14: №№ 13.112, 13.115 [2]. Тема 15: №№ 14.8, 14.11, 14.25, 14.26, 14.48, 14.50, 14.64, 14.65, 14.72, 14.60, 14.88, 14.79, 14.96, 14.108, 14.111, 14.122, 14.124, 14.127, 14.144, 14.148, 14.149, 14.152 [2]. Тема 16: №№ 15.9, 15.24, 15.41 [2]. Тема 17: №№ 15.73, 15.89 [2]. Тема 18: №№ 15.54, 15.56, 15.58, 15.67 [2]. Тема 19: №№ 16.16, 16.21, 16.25, 16.29, 16.33, 16.36, 16.38, 16.43 [2]. Тема 20: №№ 16.49, 16.56, 16.59 [2]. Тема 21: №№ 16.65 – 16.68, 16.71, 16.80, 16.83 [2]. Тема 22: №№ 17.13, 17.20, 17.22, 17.29, 17.30, 17.35, 17.43 [2]. Тема 23: №№ 17.59, 17.60 [2]. Тема 24: №№ 17.87, 17.70, 17.75, 17.77, 17.78, 17.81, 17.91, 17.94 [2].

Примерные варианты контрольных работ: Контрольная работа №1.

1. Найти все значения и изобразить их на плоскости.

2. Построить кривые: а) у = 3│ln (x – 2) + 1│ - 3; б) 25х ² – 64у ² + 50х + 128у – 1639 = 0.

3. Вычислить пределы: а) ; б) ; в) ; г) . 4. Найти производную функции у = . 5. Вычислить приближённо с помощью дифференциала . 6. Используя правила Лопиталя, вычислить предел . 7. Исследовать функцию у = и построить её график. 8. Требуется изготовить открытый цилиндрический резервуар вместимостью 300 м ³. Стоимость материала, из которого производится дно, в два раза больше стоимости материала, идущего на боковые стенки. При каких размерах резервуара его изготовление окажется более дешёвым?

Контрольная работа №2.

1. Найти экстремумы функции z = 2x³ + 6xy ² – 30x – 24y.

2. Найти неопределённые интегралы и вычислить определённые интегралы: а) ; б) ; в) ; г) .

3. Найти общие интегралы дифференциальных уравнений и, где указано, решить задачу Коши: а) 4x dx – 3y dy = 3x ²y dy - 2xy ²dx; б) y’ = + 4 + 2; в) y’ - = x ², y (1) = 0;

г) 3x ²e ^y dx + (x ³e ^y – 1) dy =0. 4. Исследовать на сходимость числовые ряды: а) ; б) . 5. Найти промежуток сходимости степенного ряда: .

Итоговый контроль знаний студента на экзамене (или зачёте) зависит от текущей успеваемости студента в течение семестра во время его самостоятельной работы на практических занятиях (включая работу у классной доски) и от оценки за итоговую контрольную работу, которая предлагается на последнем занятии (время выполнения – 180 минут). Нормативы для контрольной работы: 12 безупречно выполненных и оформленных заданий – «превосходно»; 11 или 12 выполненных заданий с правильными решениями, но с незначительными недочётами – «отлично»; 10 безупречно выполненных и оформленных заданий – «очень хорошо»; 8 или 9 выполненных заданий с правильными решениями, но с незначительными недочётами – «хорошо»; 5-7 выполненных заданий с правильными решениями, но с незначительными недочётами – «удовлетворительно»; менее 5-ти правильно выполненных заданий – «неудовлетворительно»; ни одного правильно выполненного задания – «плохо».