Статистическая обработка результатов измерения
Таблица 2. Измерение высоты образующей цилиндра
№ |
h, мм |
1 |
12,3 |
2 |
12,1 |
3 |
12,2 |
4 |
12,3 |
5 |
12,1 |
По результатам измерений определим среднее значение h:
hср 12,3 12,1 12,2 12,3 12,1 12,2 мм
5
Рассчитаем объем цилиндра по среднему значению h (возьмем число π = 3,14 – на одну цифру после запятой больше, чем в значении высоты):
Vср R2hср 3,14 (18)2 12,2 12411,792мм3
А.Н.Седов 2008 |
21 |
Статистическая обработка результатов измерения
Выведем из расчетной формулы
V R2h
формулу для вычисления относительной погрешности :
V |
V |
|
|
2 |
|
R 2 |
|
h |
2 |
|
V |
|
|
4 |
|
|
. |
||||
|
|
|
|
|
R |
|
h |
|
|
|
Относительной погрешность числа числа π можно пренебречь.
V |
V |
|
|
R 2 |
|
h |
2 |
|
V |
4 |
|
|
. |
||||
|
|
|
R |
|
h |
|
|
|
А.Н.Седов 2008 |
22 |
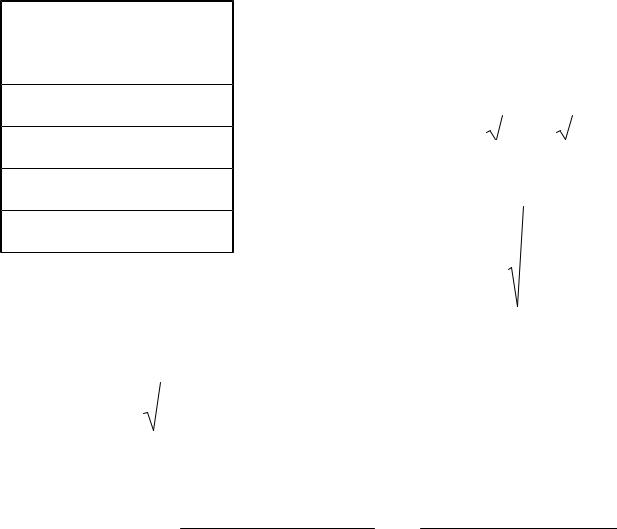
Статистическая обработка результатов измерения
№ |
h, мм |
Определим погрешность прямого измерения h. |
||||||||||
1 |
12,3 |
Погрешность средств измерения: |
|
|||||||||
|
пр |
|
|
0,1 |
|
|
||||||
2 |
12,1 |
hси |
|
|
0,068. |
|||||||
|
|
|
|
|
|
|
||||||
3 |
|
3 |
|
|||||||||
3 |
12,2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
4 |
12,3 |
Случайную погрешность hсл вычисляем по формуле |
||||||||||
5 |
12,1 |
|
|
|
|
|
n |
hi |
hср 2 |
|
||
|
|
|
|
|
|
|
||||||
|
|
hсл t p,n |
|
i 1 |
|
. |
||||||
|
|
|
|
n n 1 |
||||||||
|
|
|
|
|
|
|
|
|
||||
Для доверительной вероятности P = 0,95 и числа измерений n = 5 коэффициент Стьюдента tp,n = 2,776 (значения коэффициента Стьюдента приведены в таблице) .
h |
2,776 |
12,3 12,2 2 12,1 12,2 2 12,2 12,2 2 12,3 12,2 2 12,1 12,2 2 |
. |
сл |
|
5 4 |
|
hсл = 0,34 мм
Результирующая абсолютная погрешность:
h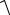 
hсл 2 hси 2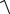 
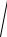0,34 2 0,068 2 0,369 мм
А.Н.Седов 2008 |
23 |
Статистическая обработка результатов измерения
Вычислим относительную погрешность измерения высоты и радиуса цилиндра:
h |
h |
0,396 |
0,033 , |
R |
R |
|
0,5 |
0,028 . |
|
hср |
R |
18 |
|||||||
|
12,2 |
|
|
|
|
Относительная погрешность объема цилиндра рассчитывается по формуле:
|
V |
4 |
R 2 |
|
|
h 2 |
|
|
|
|
|
|
4 0,028 2 0,033 2 |
0,065 |
|||||
V |
V |
|
|
|
|
|
|
|
|
|
|
R |
|
|
h |
|
|
|
Вычислим абсолютную погрешность измерения объема цилиндра:V = δVVср = 0,065·12411,792 = 806,767 мм3.
Vср = 12411,792 мм3.
Как правильно округлить значение погрешности и среднего значения?
А.Н.Седов 2008 |
24 |
Правила округления результатов измерений
Сначала округляется значение абсолютной погрешности:
– если первая значащая цифра 1 или 2, то значение погрешности округляется до двух значащих цифр;
13,85 |
14 |
|
|
|
первая цифра 1 |
Округляем до двух цифр |
|
0, 125 0,13 |
1,037 1,0 |
0,235 0,24 |
165,43 1,7 102 |
– если первая значащая цифра 3, 4,... , 9, то значение погрешности округляется до одной значащей цифры.
3,85 
4
первая цифра 3 Округляем до одной цифры
0,502 0,5 |
7,434 7 |
0,045 0,05 |
735,32 7 102 |
А.Н.Седов 2008 |
25 |
Правила округления результатов измерений
Затем округляется среднее значение измеряемой величины:
- последняя значащая цифра в среднем значении должна стоять в том же разряде, что и последняя значащая цифра в округленном значении абсолютной погрешности.
Среднее значение: |
163,248 мм |
Погрешность: 0,235 мм |
163,25 мм |
0,24 мм |
l = ( 163,25 0,24) мм
(467,202 0,502) (467,2 0,5)
(123,072 1,04) (123,1 1,0)
(1234,5 165,4) (1,23 0,17) 103
А.Н.Седов 2008 |
26 |
Запись окончательного результата измерений
Запишем окончательный результат измерения объема цилиндра:
V = 806,767 мм3
Vср = 12411,792 мм3
V = (124 ± 8)·102 мм3, Р = 0,95
или
V = (12,4 ± 0,8) см3, |
Р = 0,95 |
А.Н.Седов 2008 |
27 |