
- •Высшая математика Методические указания к практическим занятиям по теме «Векторная алгебра и элементы аналитической геометрии» для студентов дневной и заочной форм обучения всех специальностей
- •212005, Г. Могилев, пр. Мира, 43
- •Содержание
- •Введение
- •1 Линейные операции над векторами, линейная зависимость и независимость векторов.
- •Линейные операции над векторами, линейная зависимость и независимость векторов
- •Линейные операции над векторами
- •Линейная зависимость и независимость векторов
- •Упражнения
- •Контрольные задания
- •Базисы и координаты векторов. Скалярное произведение векторов
- •Базисы и координаты векторов
- •Скалярное произведение векторов
- •Упражнения
- •Контрольные задания
- •Векторное произведение векторов. Смешанное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Упражнения
- •Контрольные задания
- •Прямая на плоскости
- •Основные способы задания прямых на плоскости
- •Упражнения
- •Контрольные задания
- •Плоскость в пространстве
- •Основные способы задания плоскостей
- •Упражнения
- •Контрольные задания
- •Прямая в пространстве
- •Основные способы задания прямой в пространстве
- •Взаимное расположение двух прямых
- •Упражнения
- •Контрольные задания
- •Список литературы
-
Упражнения
-
Составить уравнение прямой, проходящей через точки
 и
и
 и сделать чертеж:
и сделать чертеж:
-
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() .
.
-
Составить параметрические уравнения прямой
 .
. -
Прямая задана параметрическими уравнениями

Найти нормальный вектор этой прямой и записать общее уравнение этой прямой.
-
Дана прямая
 .
Составить уравнения прямых, проходящих
через точку
.
Составить уравнения прямых, проходящих
через точку
 параллельно и перпендикулярно данной
прямой.
параллельно и перпендикулярно данной
прямой. -
Известны вершины треугольника
 ,
,
 ,
,
 .
.
Требуется:
1) написать уравнения сторон этого треугольника;
2) написать уравнение высоты AD и найти её длину;
3) написать уравнение медианы BF и найти её длину;
4) найти угол при вершине A треугольника;
5) найти угол между высотой AD и медианой BF.
-
Вычислить расстояние от точки
 до прямой
до прямой
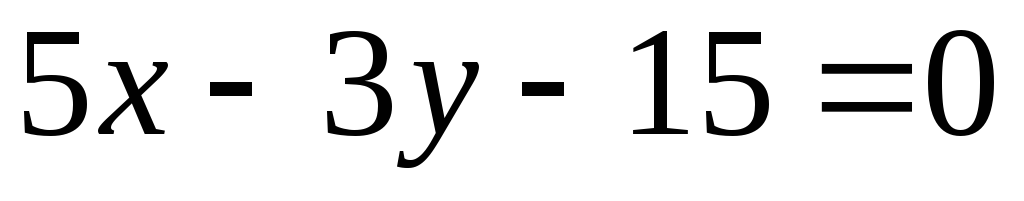 .
. -
Написать уравнение прямой, проходящей посередине между параллельными прямыми
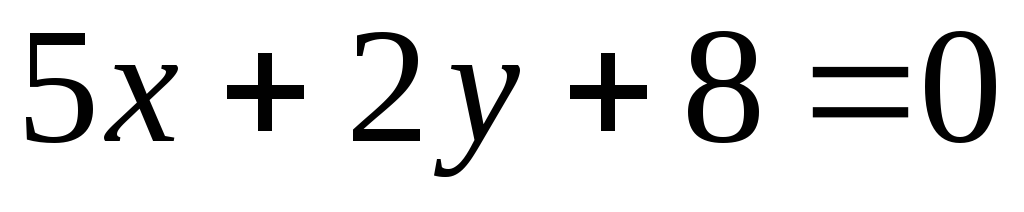 и
и
 .
. -
Написать уравнение прямой, параллельной прямой
 и отстоящей от неё на расстоянии
и отстоящей от неё на расстоянии

-
Записать уравнение прямой, проходящей через точку
 под углом
под углом
 к прямой
к прямой
 .
. -
Известны уравнения одной из сторон ромба и одной из его диагоналей:
 ,
,
 .
Известна точка пересечения его
диагоналей
.
Известна точка пересечения его
диагоналей
 .
Найти уравнения остальных сторон
ромба.
.
Найти уравнения остальных сторон
ромба.
-
Контрольные задания
Рекомендуемая литература [1, гл. 2, §2–3], [2, гл. 5, §5.1–5.7].
-
Даны вершины треугольника
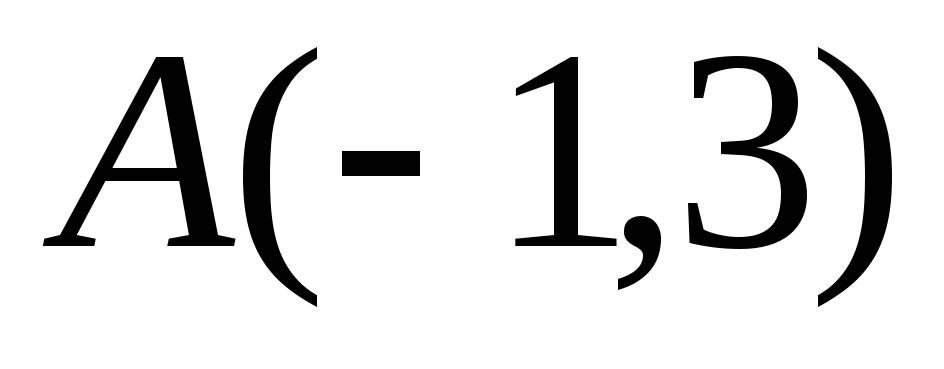 ,
,
 ,
,
 .
.
Требуется:
1) написать уравнения сторон этого треугольника;
2) написать уравнение высоты CD, проведённой из вершины C;
3) написать уравнение медианы BF, проведённой из вершины B;
4) найти угол при вершине A треугольника;
5) построить на чертеже
![]() ,
высоту СD и медиану
BF.
,
высоту СD и медиану
BF.
-
Вычислить расстояние от точки
 до прямой
до прямой
 .
. -
Известно уравнение одной из сторон параллелограмма
 и уравнение двух его диагоналей
и уравнение двух его диагоналей
 ,
,
 .
Найти уравнения остальных сторон
параллелограмма.
.
Найти уравнения остальных сторон
параллелограмма.
-
Плоскость в пространстве
Цель занятия: усвоение способов задания плоскости в пространстве, выработка навыков решения задач, связанных с построением плоскостей в пространстве.
-
Основные способы задания плоскостей
Считаем,
что в пространстве задана ортонормированная
система координат
![]() .
Координаты произвольной точки M
обозначаем, как правило,
.
Координаты произвольной точки M
обозначаем, как правило,
![]() .
Основной результат о задании плоскости
в пространстве заключается в следующем.
.
Основной результат о задании плоскости
в пространстве заключается в следующем.
-
Теорема. Любая плоскость в пространстве может быть задана линейным уравнением вида
![]() . (20)
. (20)
Наоборот, каждое уравнение вида (20) задает в пространстве некоторую плоскость.
Отметим,
что вектор
![]() ортогонален плоскости (20) и называется
нормальным вектором этой плоскости.
Уравнение (20) называют общим уравнением
плоскости. Различные модификации
уравнения (20) связаны с различными
способами задания плоскости. При решении
задач, связанных с использованием
плоскостей, следует выбирать тот способ
задания плоскости, который в данном
случае наиболее эффективен. Перечислим
основные способы задания плоскостей.
ортогонален плоскости (20) и называется
нормальным вектором этой плоскости.
Уравнение (20) называют общим уравнением
плоскости. Различные модификации
уравнения (20) связаны с различными
способами задания плоскости. При решении
задач, связанных с использованием
плоскостей, следует выбирать тот способ
задания плоскости, который в данном
случае наиболее эффективен. Перечислим
основные способы задания плоскостей.
-
Плоскость П определяется одной своей точкой
 и своим нормальным вектором
и своим нормальным вектором
 .
Уравнение имеет вид:
.
Уравнение имеет вид:
![]() . (21)
. (21)
-
Плоскость П определяется тремя своими точками
 ,
,
 ,
,
 .
Её уравнение имеет вид:
.
Её уравнение имеет вид:
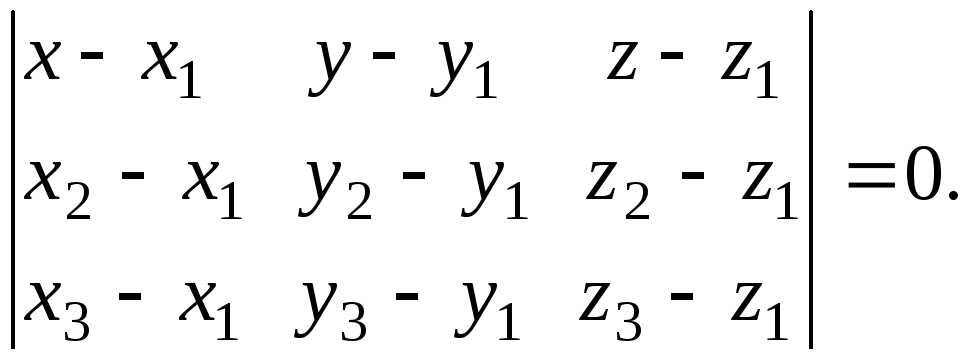 (22)
(22)
-
Плоскость П определяется двумя своими точками
 ,
,
 и вектором
и вектором
 ,
параллельным этой плоскости. Уравнение
плоскости имеет вид:
,
параллельным этой плоскости. Уравнение
плоскости имеет вид:
 (23)
(23)
-
Плоскость П определяется одной своей точкой
 и двумя векторами
и двумя векторами
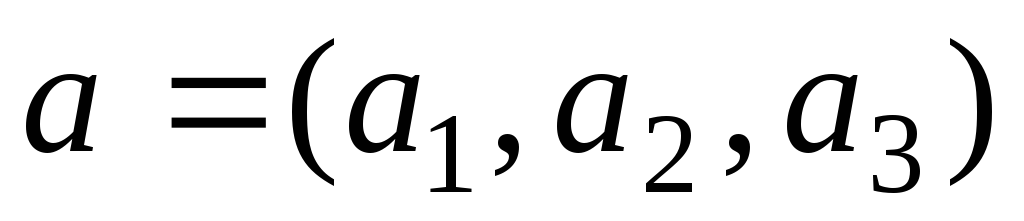 ,
,
 ,
параллельными этой плоскости. Уравнение
плоскости П имеет вид:
,
параллельными этой плоскости. Уравнение
плоскости П имеет вид:
 (24)
(24)
При решении задач
полезно использовать признаки взаимного
расположения плоскостей. Пусть П1: ![]() и П2:
и П2: ![]() – две плоскости. Эти плоскости:
– две плоскости. Эти плоскости:
1) совпадают, если
![]() ;
;
2) параллельны, если
![]() ,
т.е. если векторы
,
т.е. если векторы
![]() и
и
![]() коллинеарны;
коллинеарны;
3) пересекаются, если
их нормальные векторы
![]() и
и
![]() неколлинеарны.
неколлинеарны.
Угол
между двумя плоскостями П1
и П2
следует искать как угол между их
нормальными векторами
![]() и
и
![]() .
.
-
П
 ример.
Составить уравнение плоскости, которая
проходит через точку
ример.
Составить уравнение плоскости, которая
проходит через точку
 и перпендикулярна плоскостям
и перпендикулярна плоскостям
 ,
,
 .
.
Решение.
Нормальные векторы
![]() ,
,
![]() непараллельны, поэтому плоскости П1
и П2
пересекаются. Плоскость П, перпендикулярная
к каждой из плоскостей П1
и П2 ,
перпендикулярна и к линии их пересечения
(рисунок 8). На основании этого найдем
нормальный вектор
непараллельны, поэтому плоскости П1
и П2
пересекаются. Плоскость П, перпендикулярная
к каждой из плоскостей П1
и П2 ,
перпендикулярна и к линии их пересечения
(рисунок 8). На основании этого найдем
нормальный вектор
![]() искомой плоскости П как векторное
произведение
искомой плоскости П как векторное
произведение
![]() и
и
![]() :
:

![]()
Используя (21), запишем уравнение плоскости П:
![]() ,
,
![]() .
.
Возможен
и другой вариант решения. Пусть
![]() произвольная точка искомой плоскости.
Тогда векторы
произвольная точка искомой плоскости.
Тогда векторы
![]() ,
,
![]() ,
,
![]() компланарны, поэтому
компланарны, поэтому

![]() ,
,
![]() .
.
