ПРЕДИСЛОВИЕ РЕДАКТОРОВ

ПРЕДИСЛОВИЕ АВТОРОВ

Часть I

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

§ 1. Множества

§ 2. Необходимые и достаточные условия. Обратные и противоположные теоремы

§ 3. Последовательность. Предел последовательности

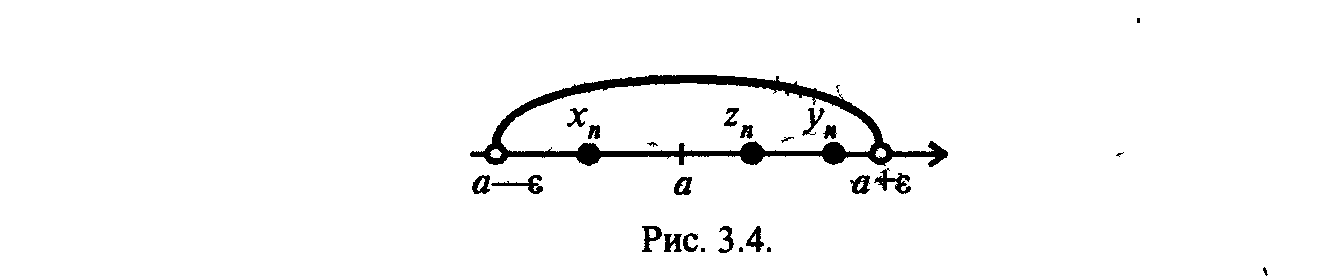
§ 4. Бесконечно большие и бесконечно малые последовательности

§ 6. Монотонные последовательности

§ 7. Подпоследовательности

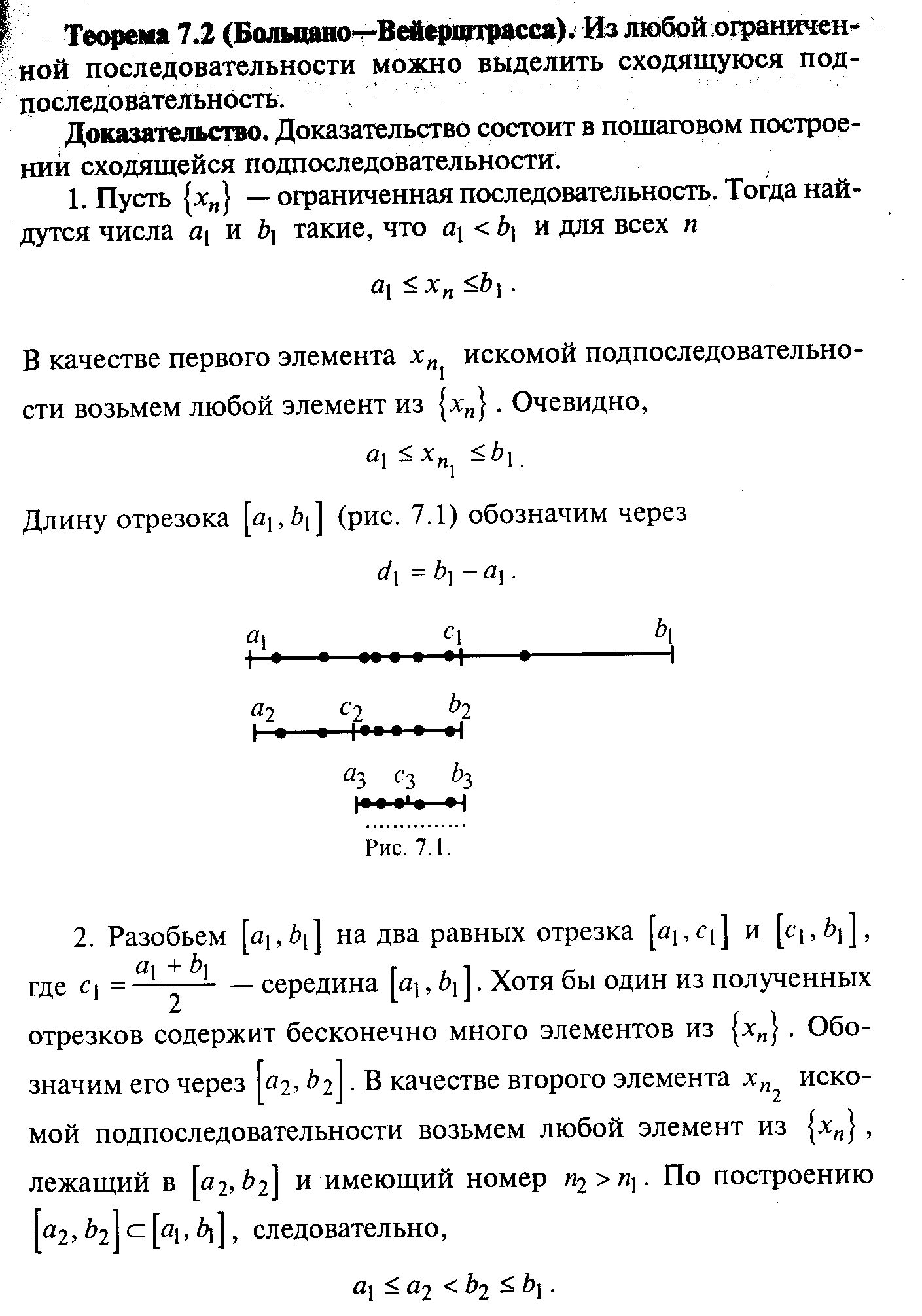
§ 8. Число е

§ 9. Понятие функции. Основные определения

§ 10. Взаимно-однозначная функция. Обратная функция

§ 11. Предел функции

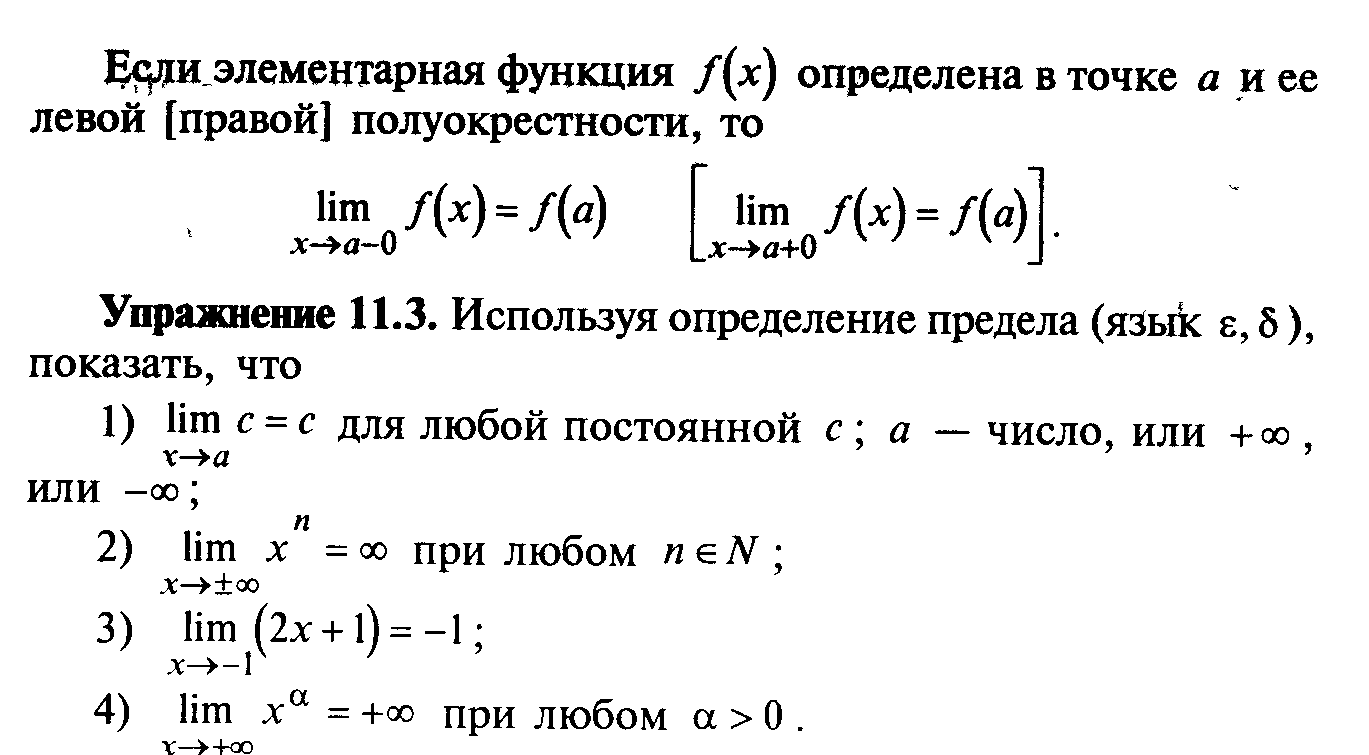
§ 12. Бесконечно большие и бесконечно малые функции. Сравнение бесконечно малых. Неопределенные выражения

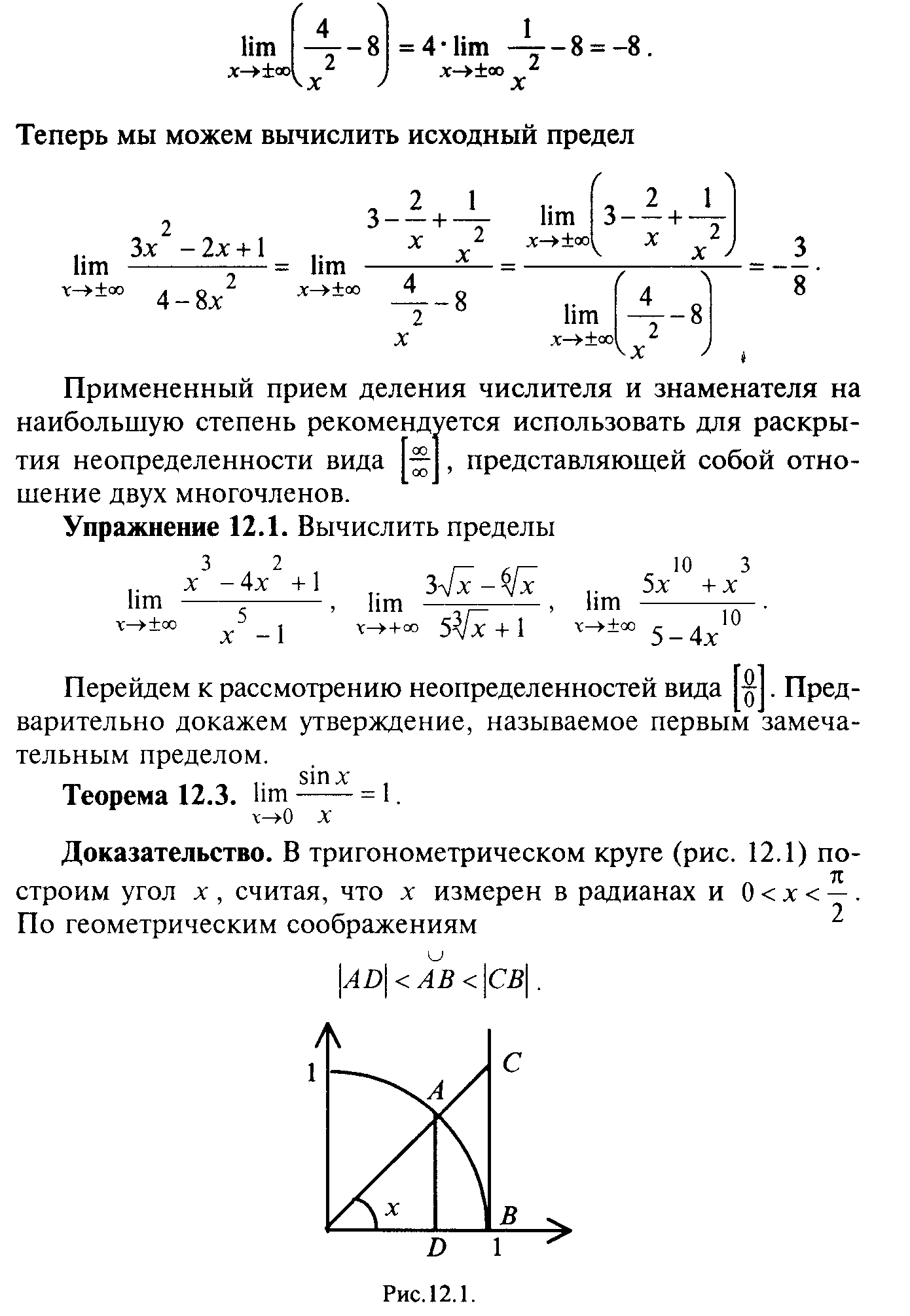
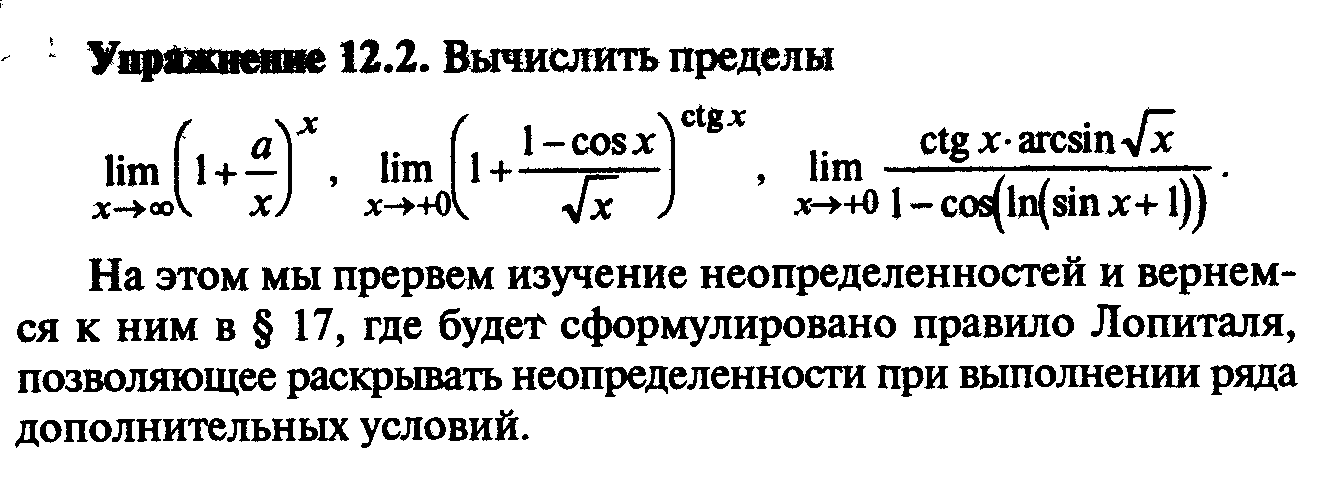
§13. Непрерывные функции. Точки разрыва и их классификация

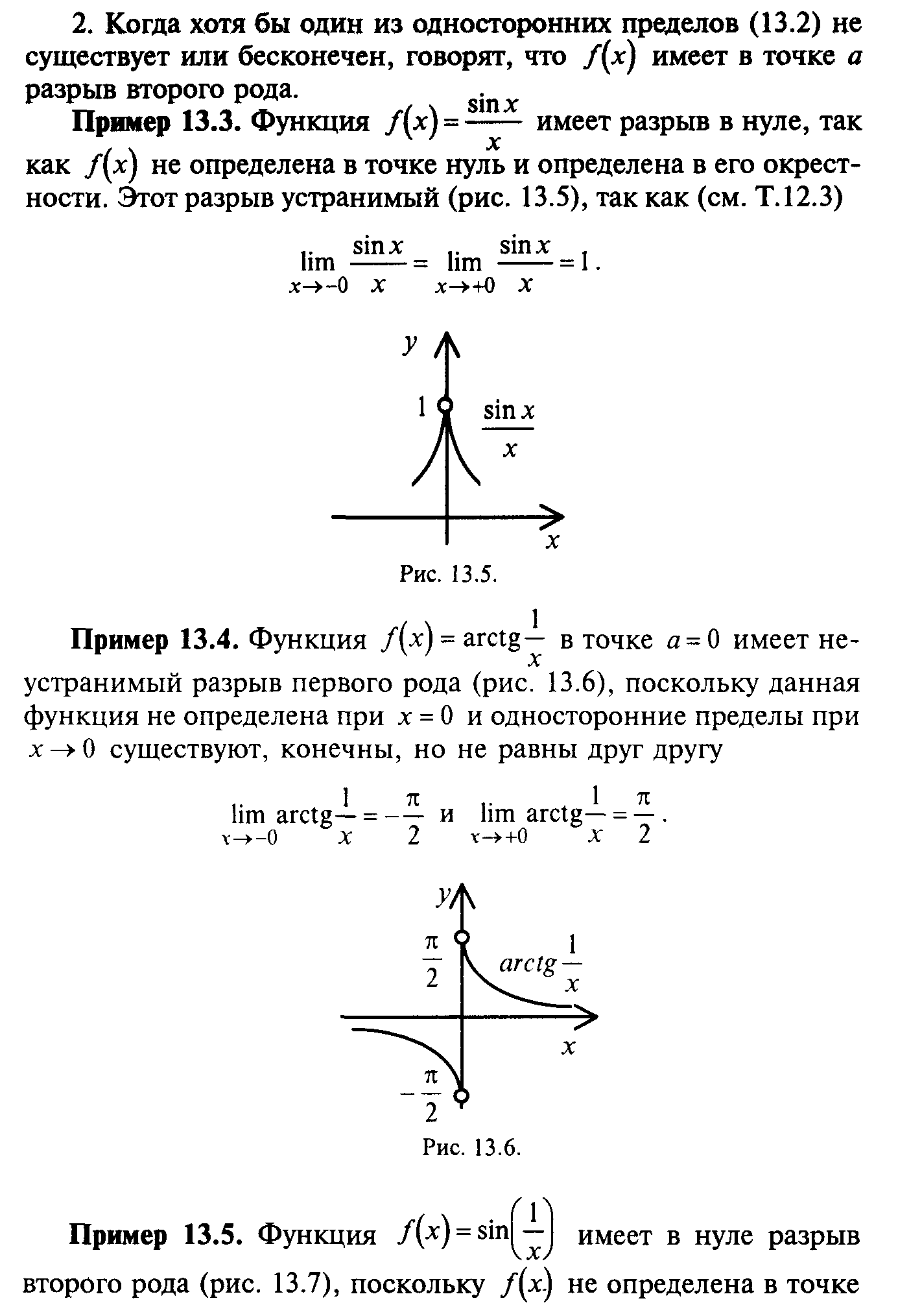
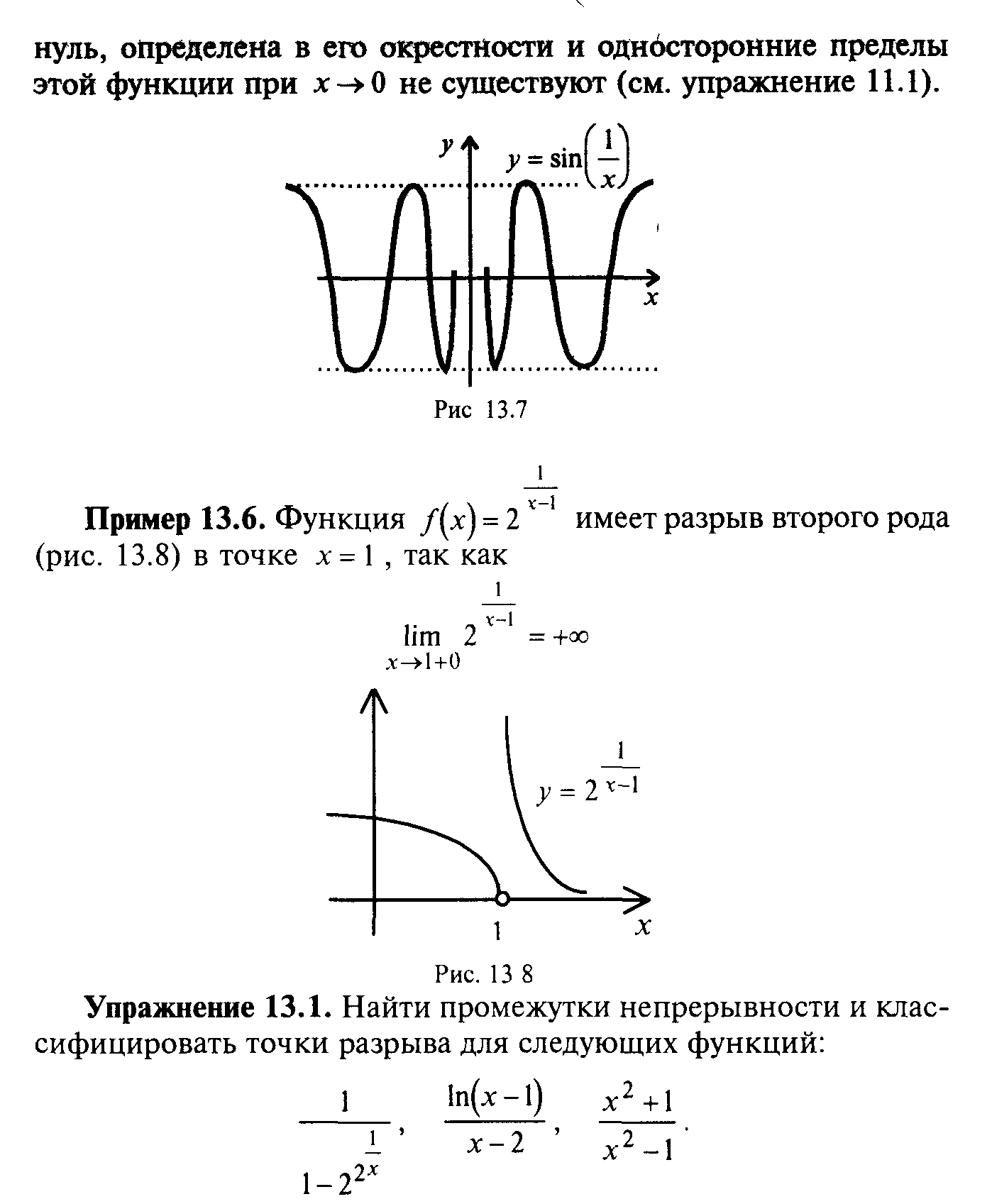
§14. Свойства функций, непрерывных на отрезке

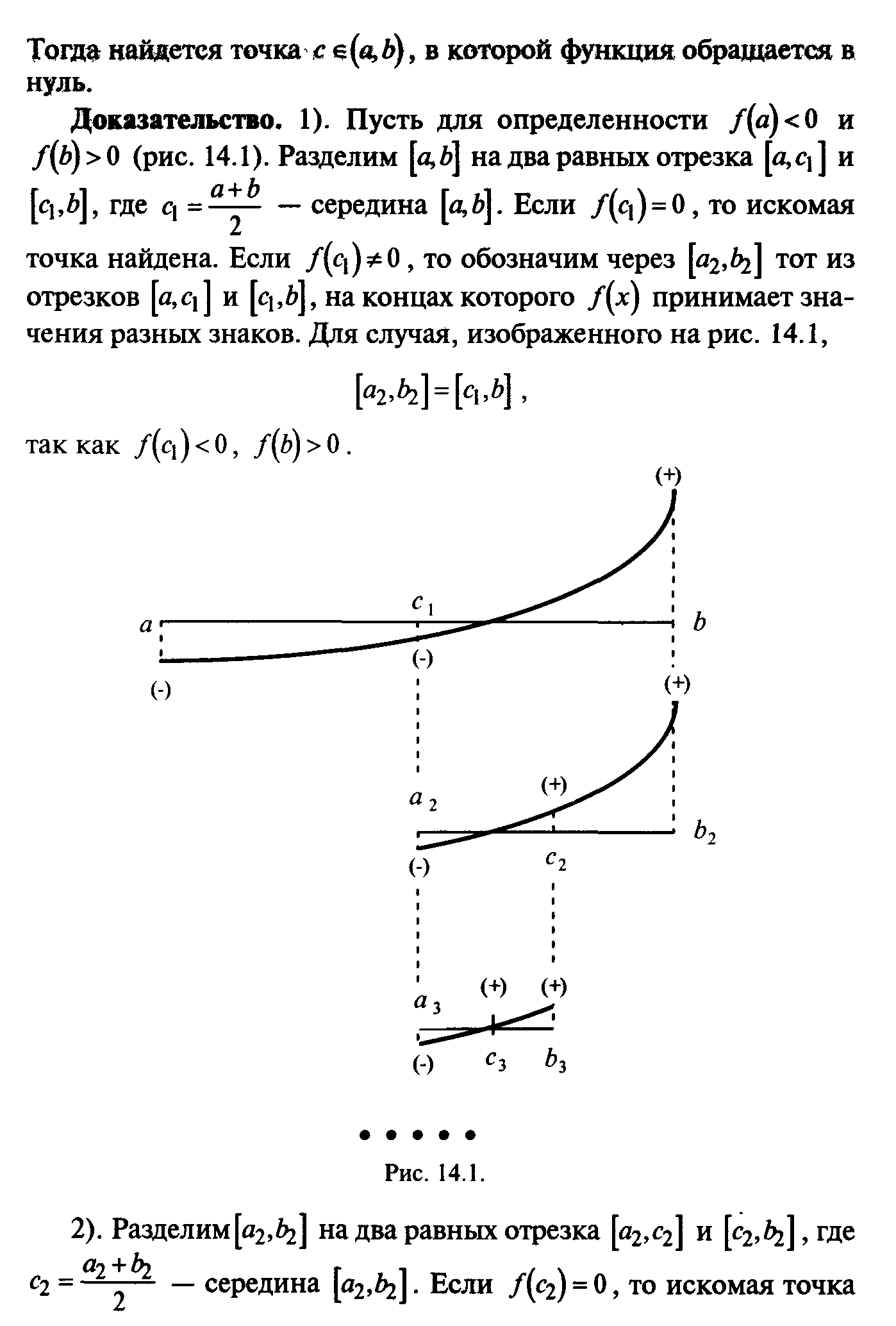
§15. Дифференцируемость функции. Производная и дифференциал

§16. Простейшие свойства производной

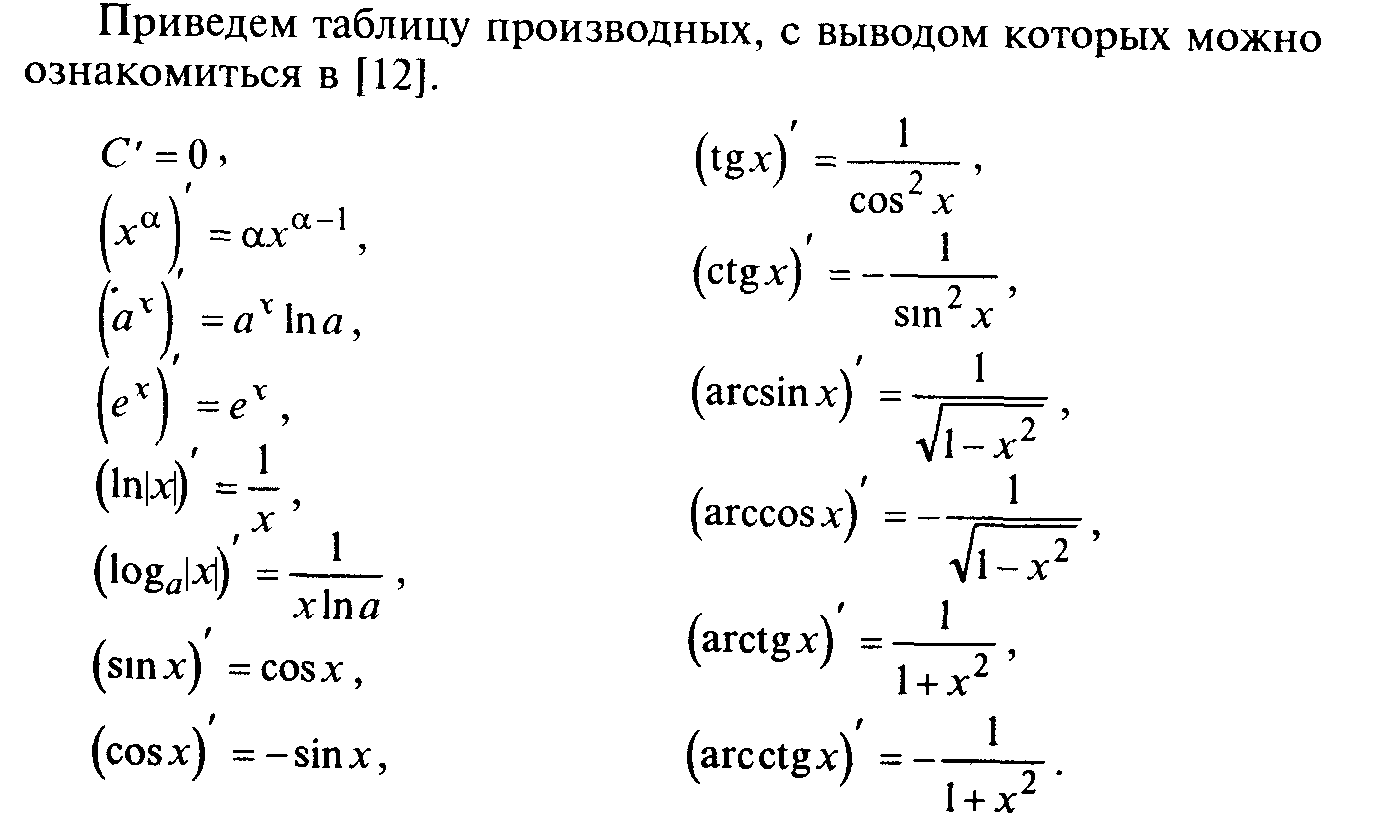
§17. Основные теоремы дифференциального исчисления

§ 18. Производные и дифференциалы высших порядков. Формула Тейлора

§19. Монотонность функции. Точки экстремума. Наибольшее и наименьшее значение функции на отрезке

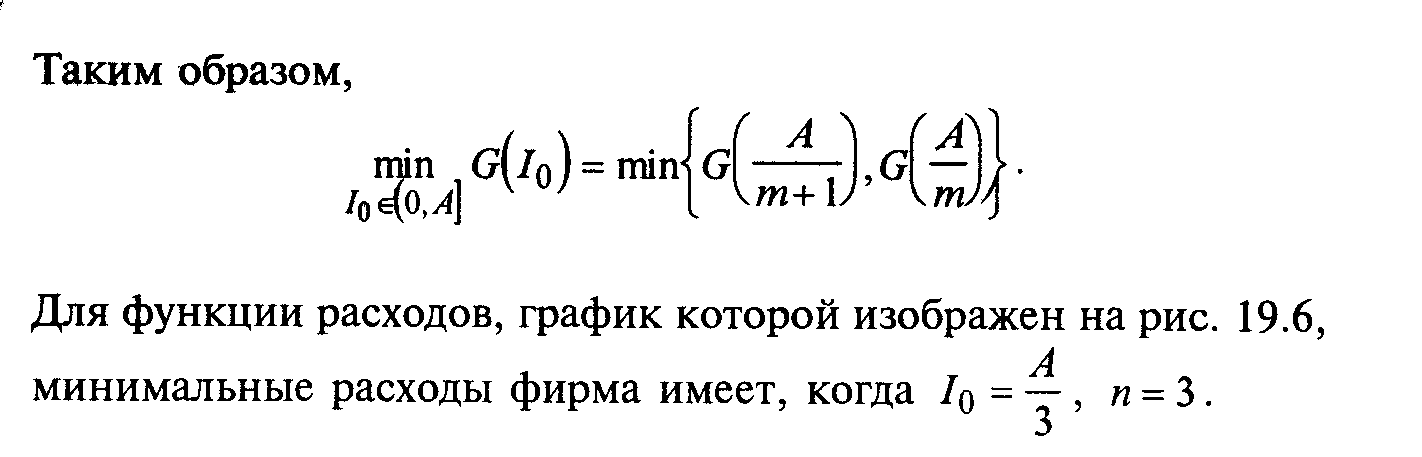
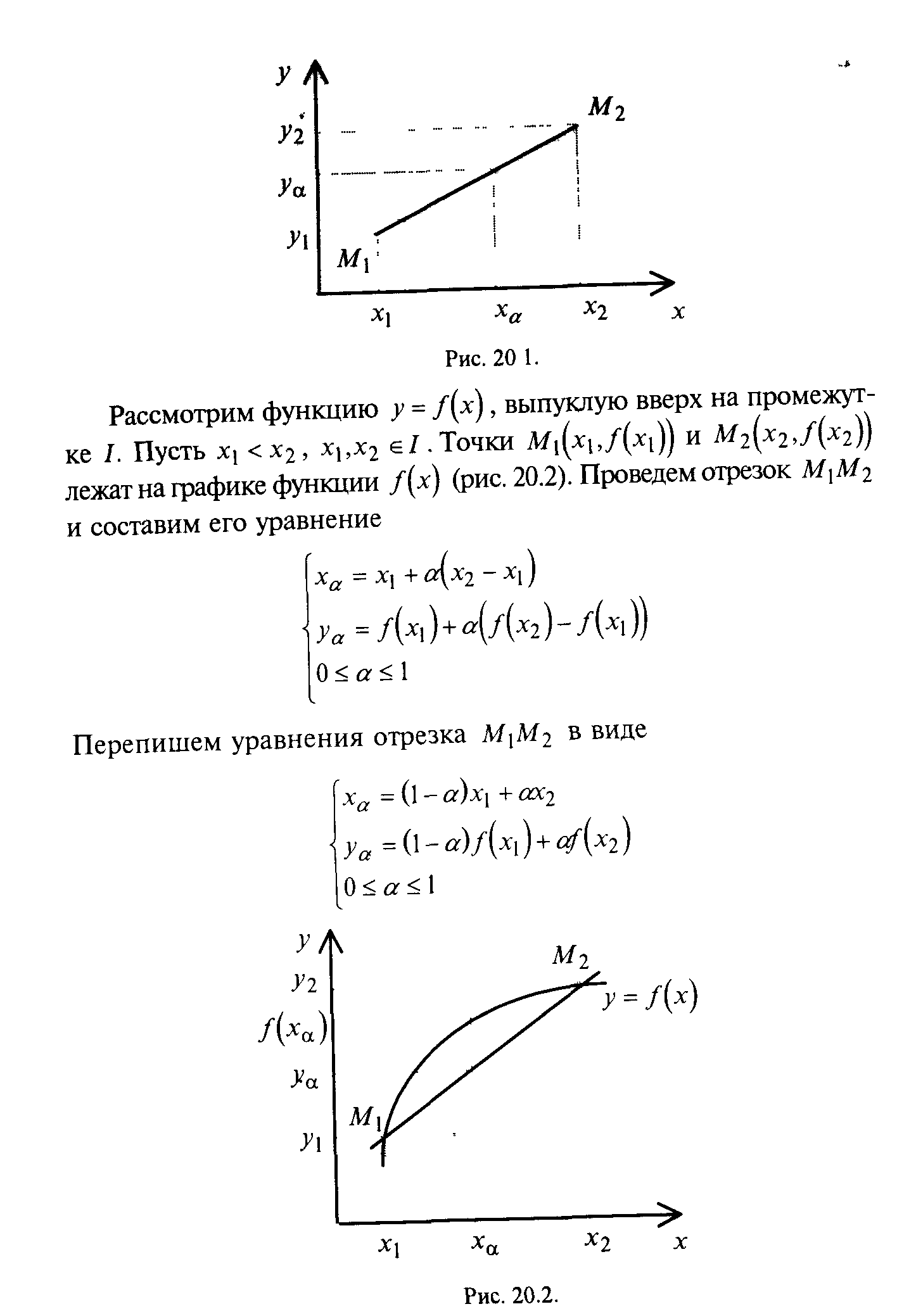
§ 20. Выпуклость функции

§ 21. Асимптоты

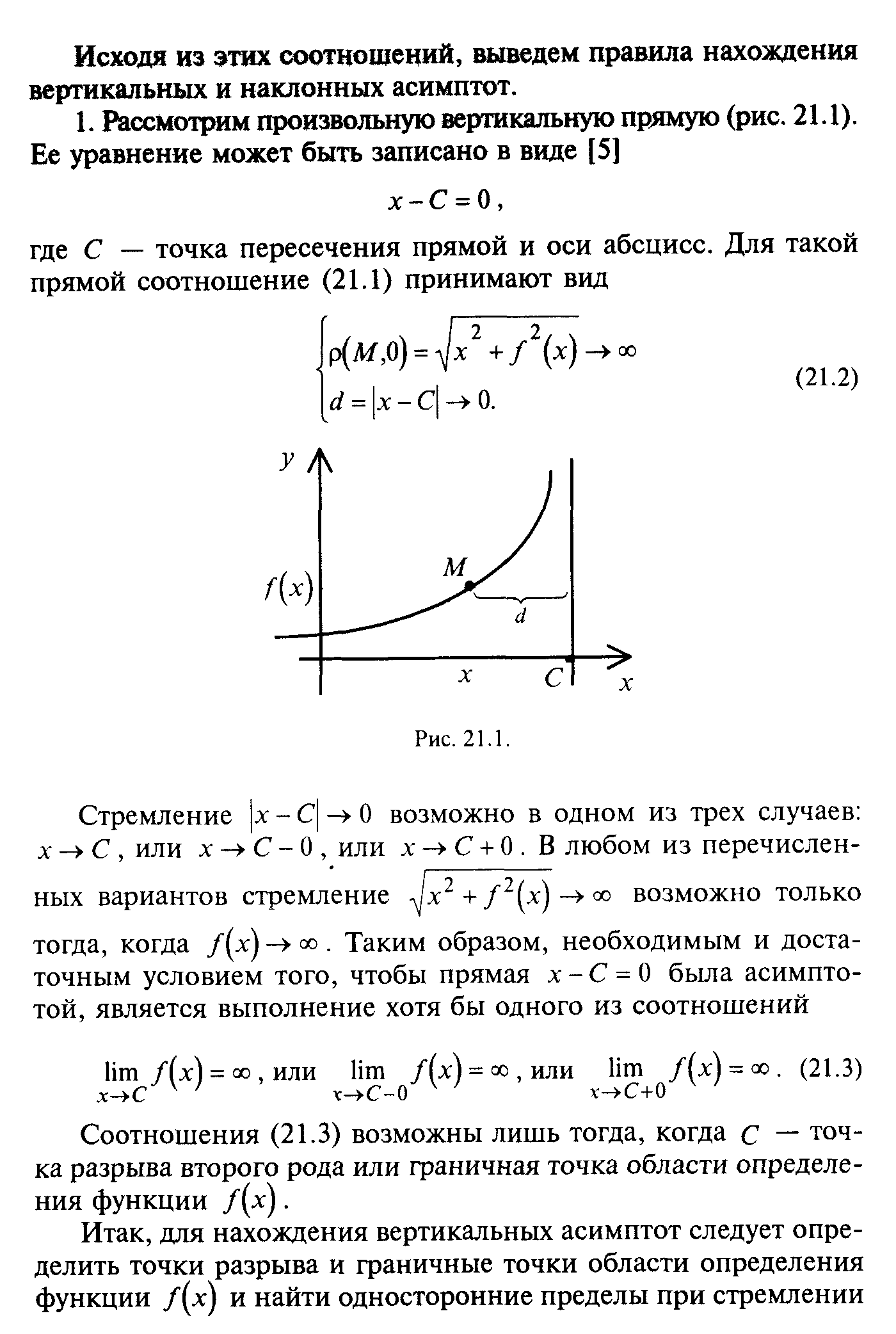
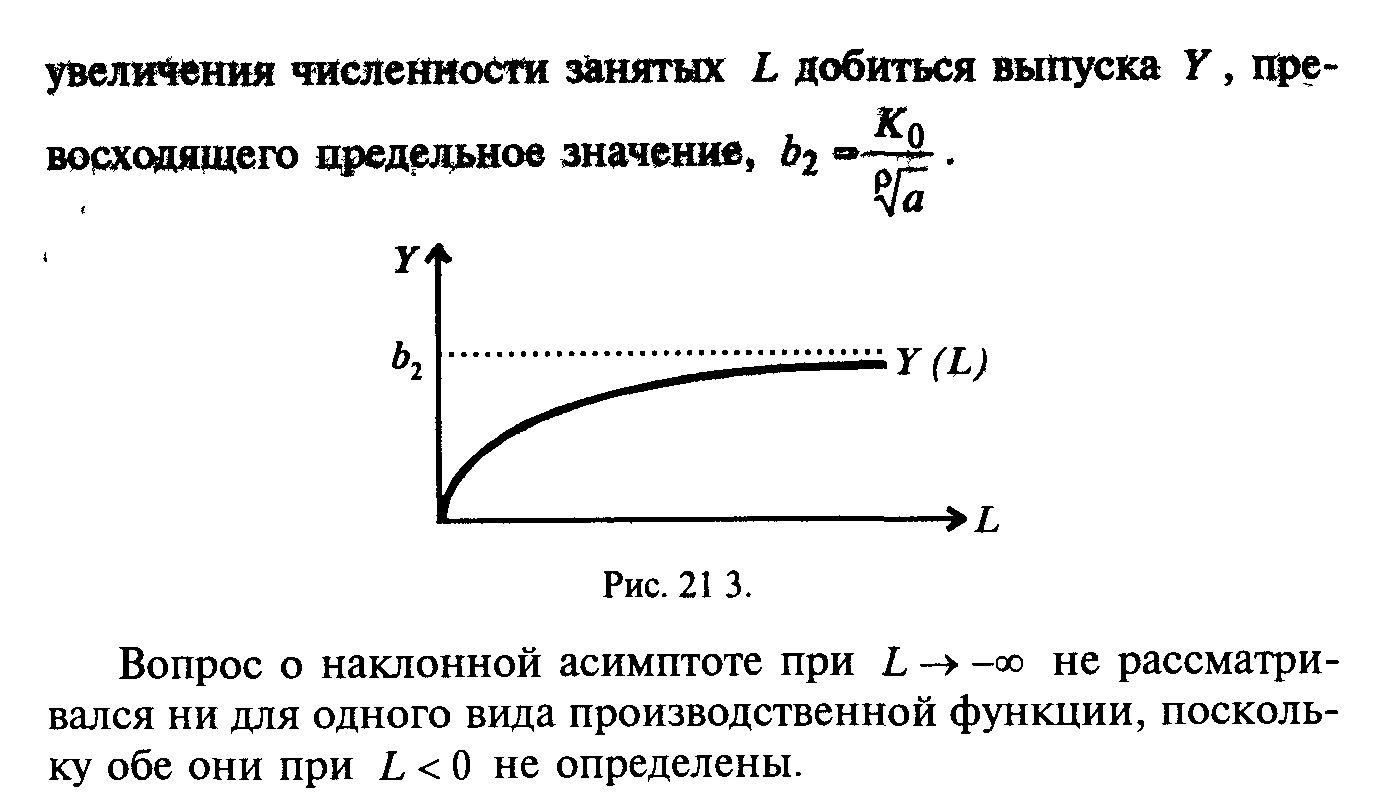
§ 22. Схема исследования функции и построения графика

§ 23. Эластичность функций

Часть II

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

§ 1. Множества в пространстве JK"

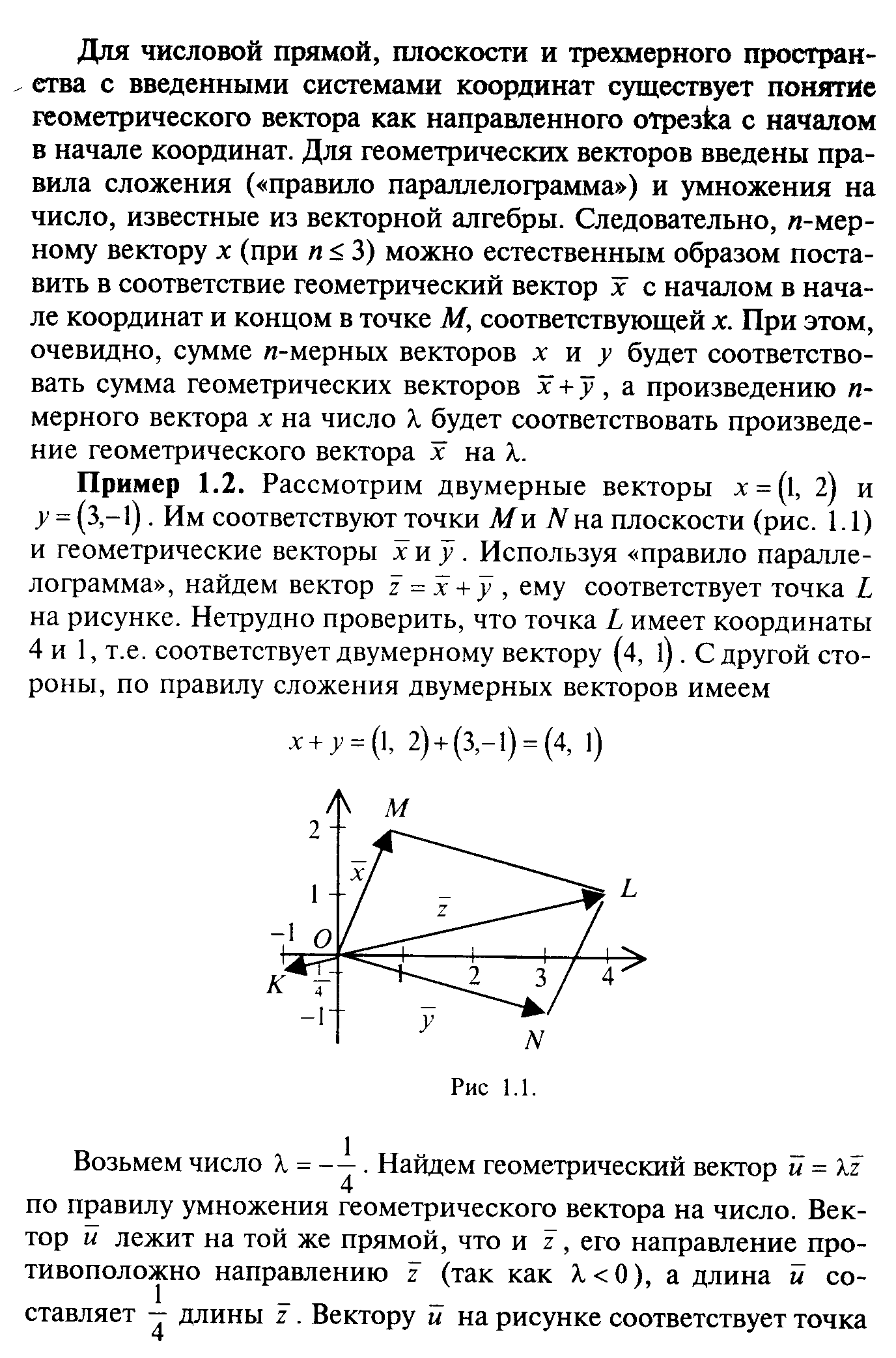
§ 2. Функции нескольких переменных. Экономические примеры

§ 3. Предел и непрерывность функций нескольких переменных

§ 4. Частные производные и эластичность функций нескольких переменных

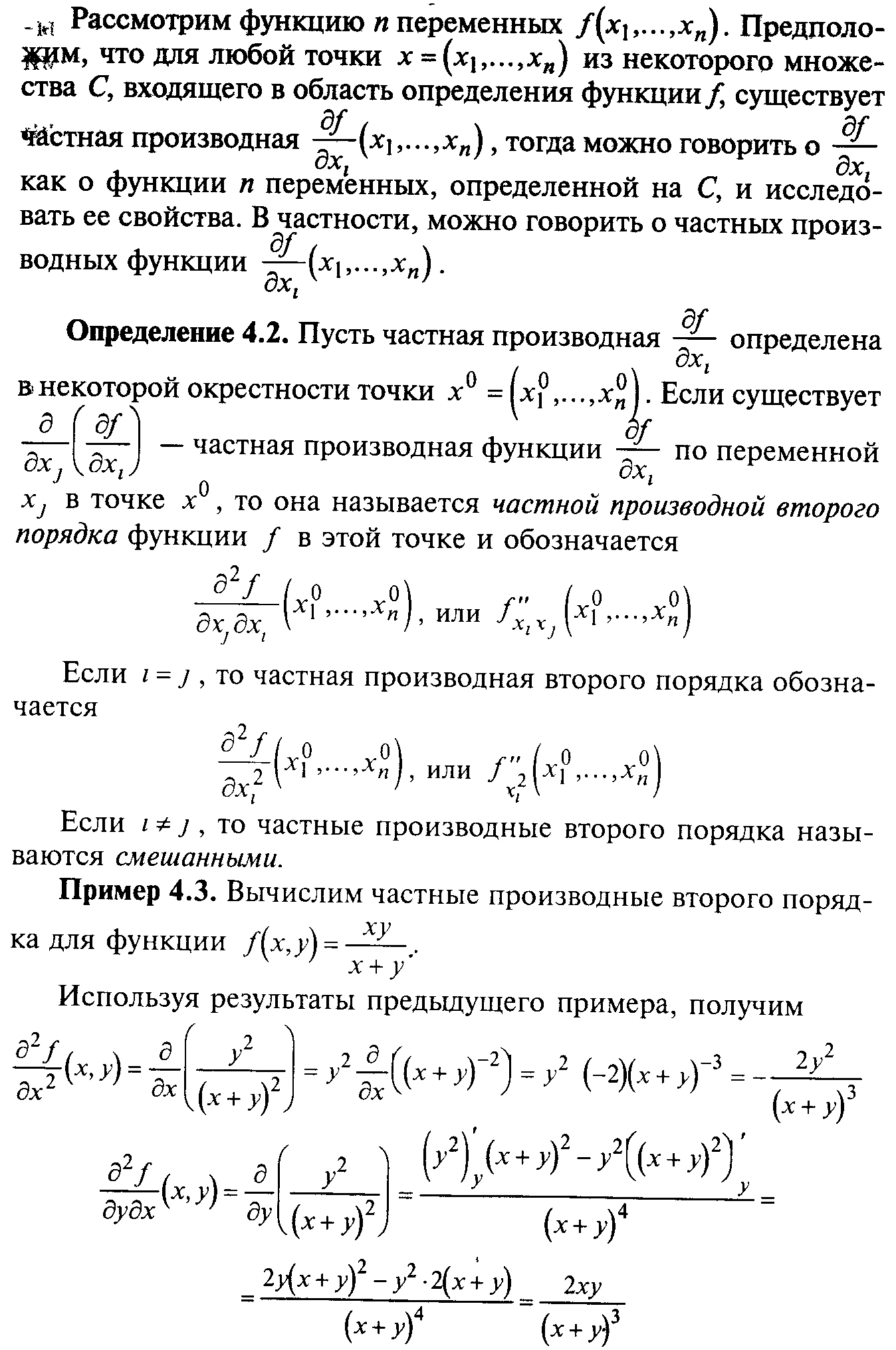
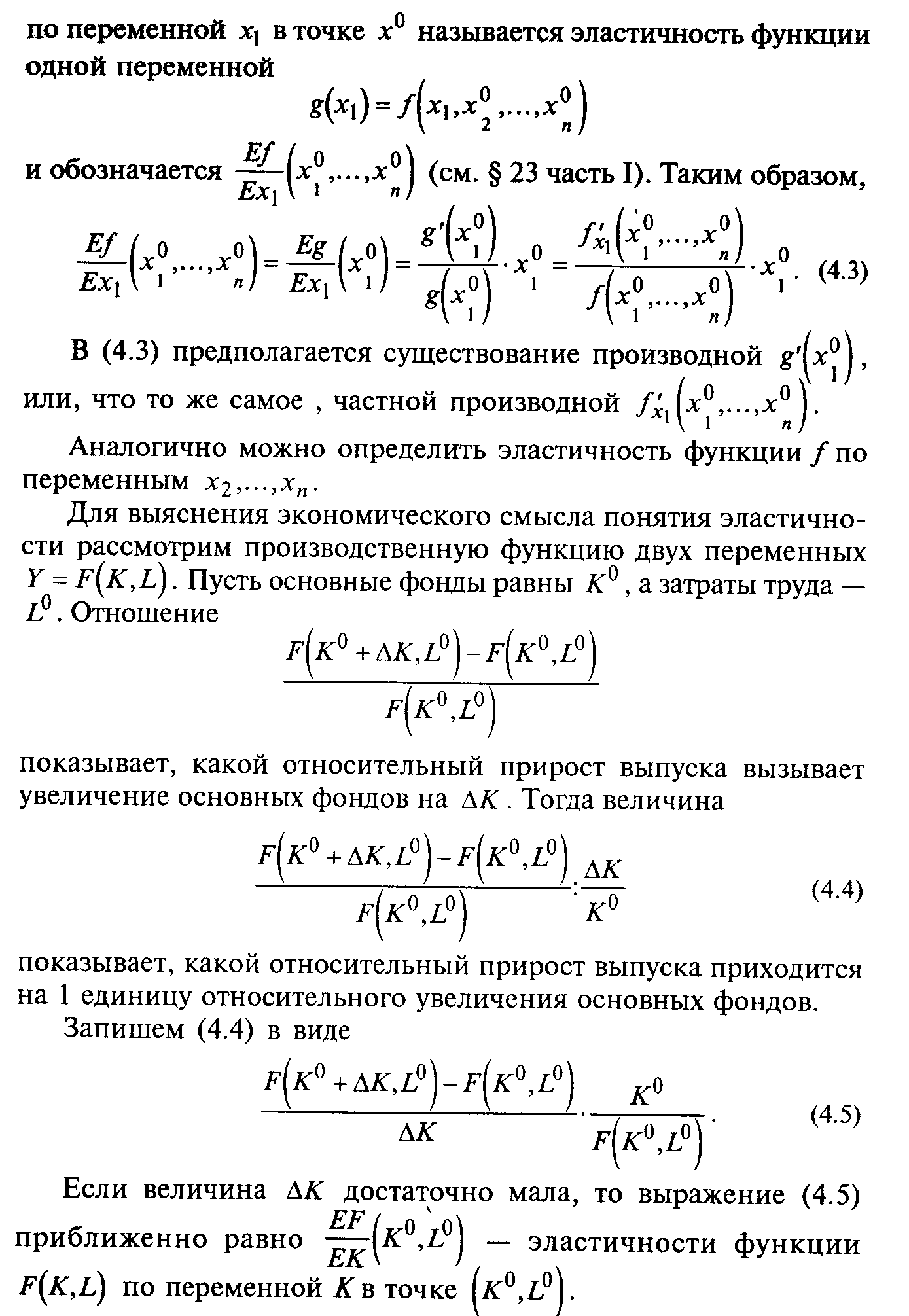
§5. Дифференцируемость функций нескольких переменных. Полный дифференциал

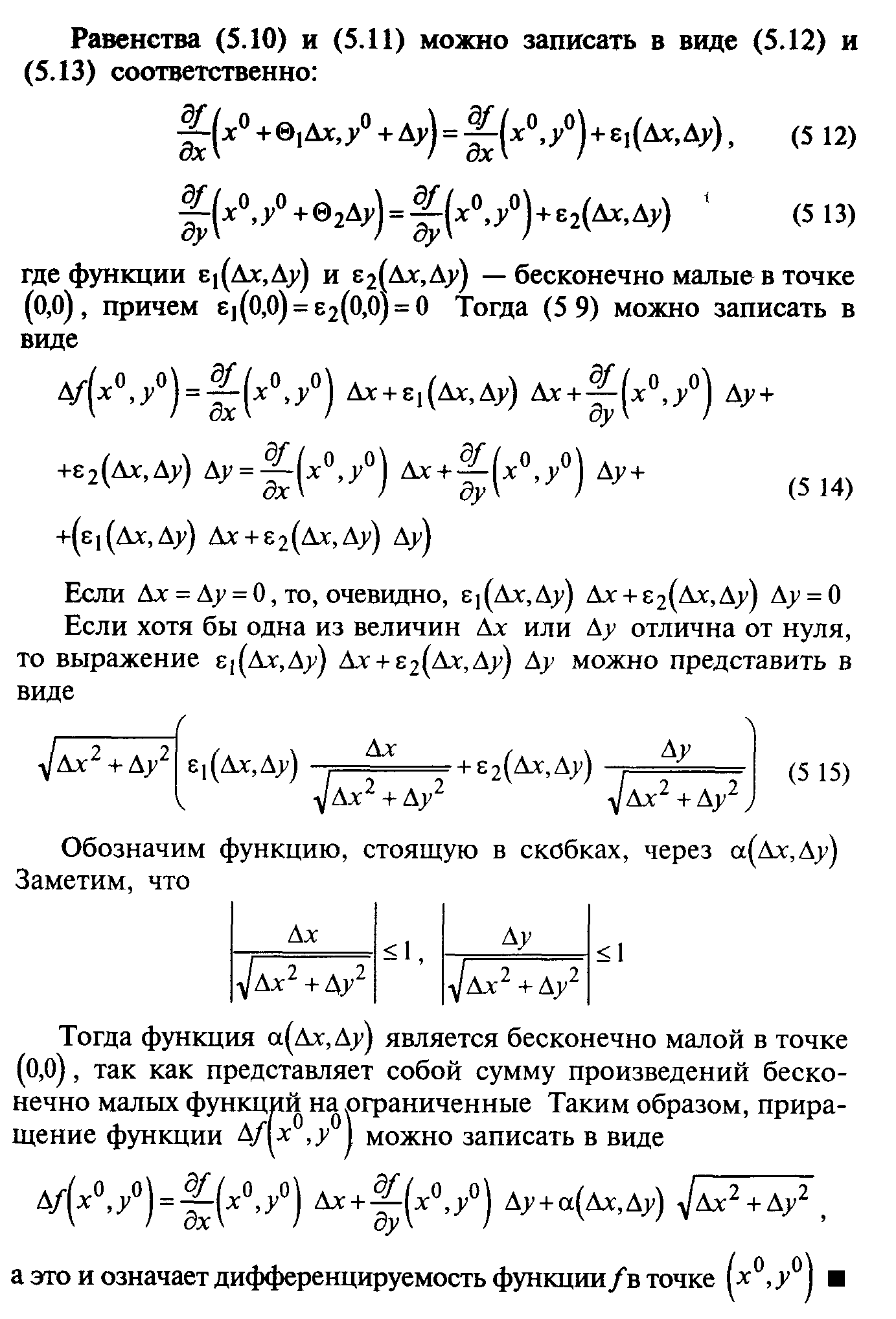
§ 6. Частные производные сложной функции

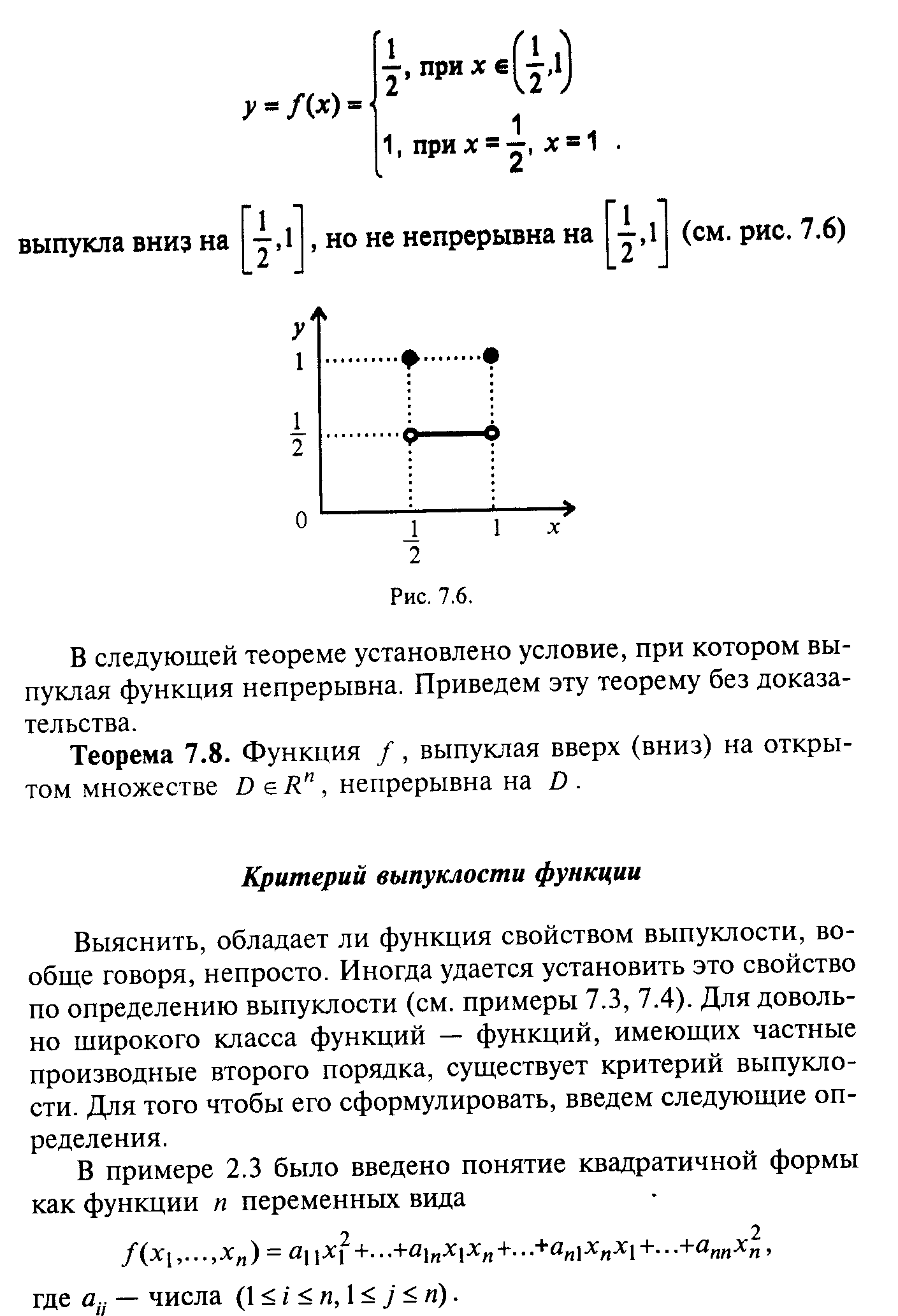
§ 7. Выпуклость функций нескольких переменных

§ 9. Неявные функции

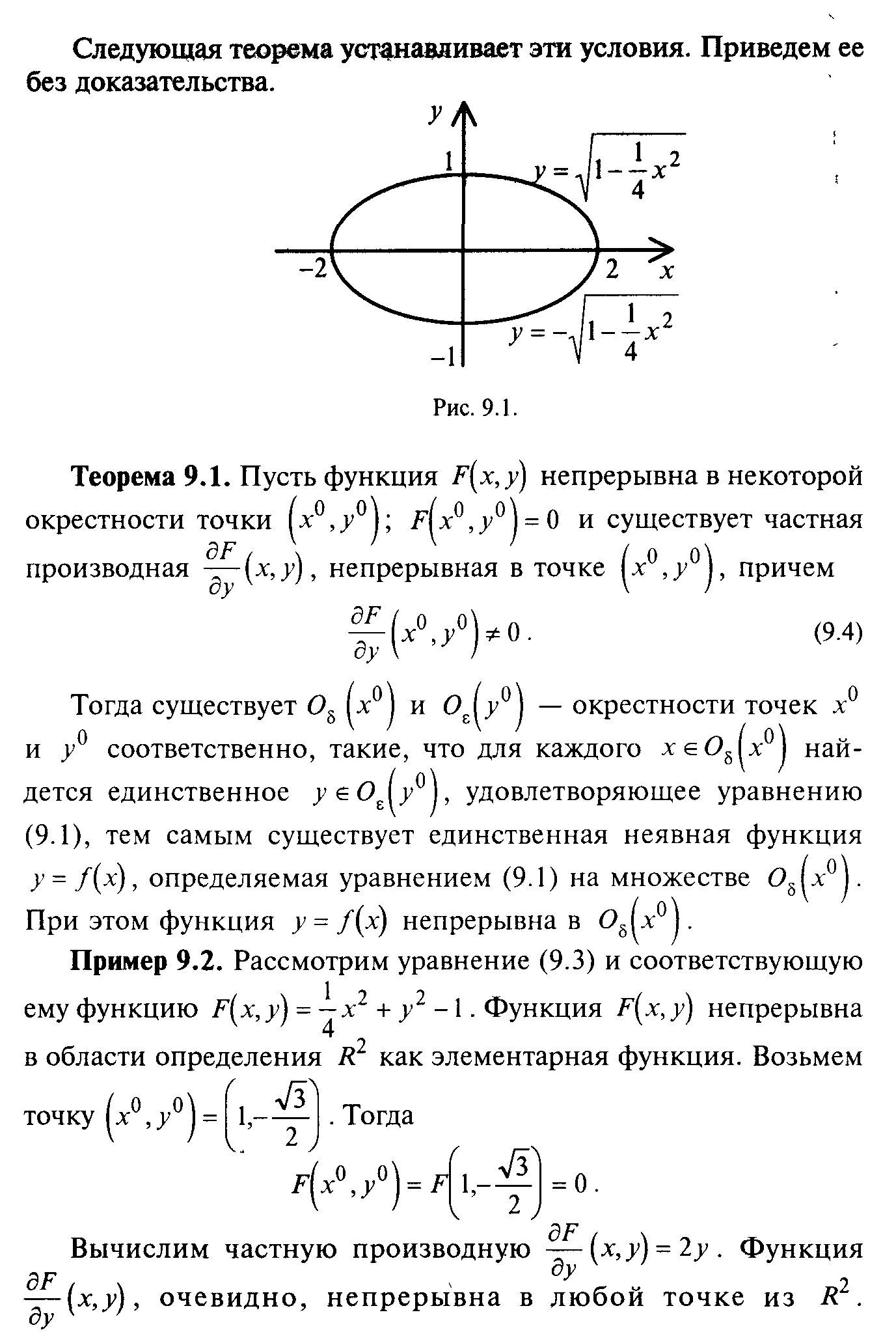
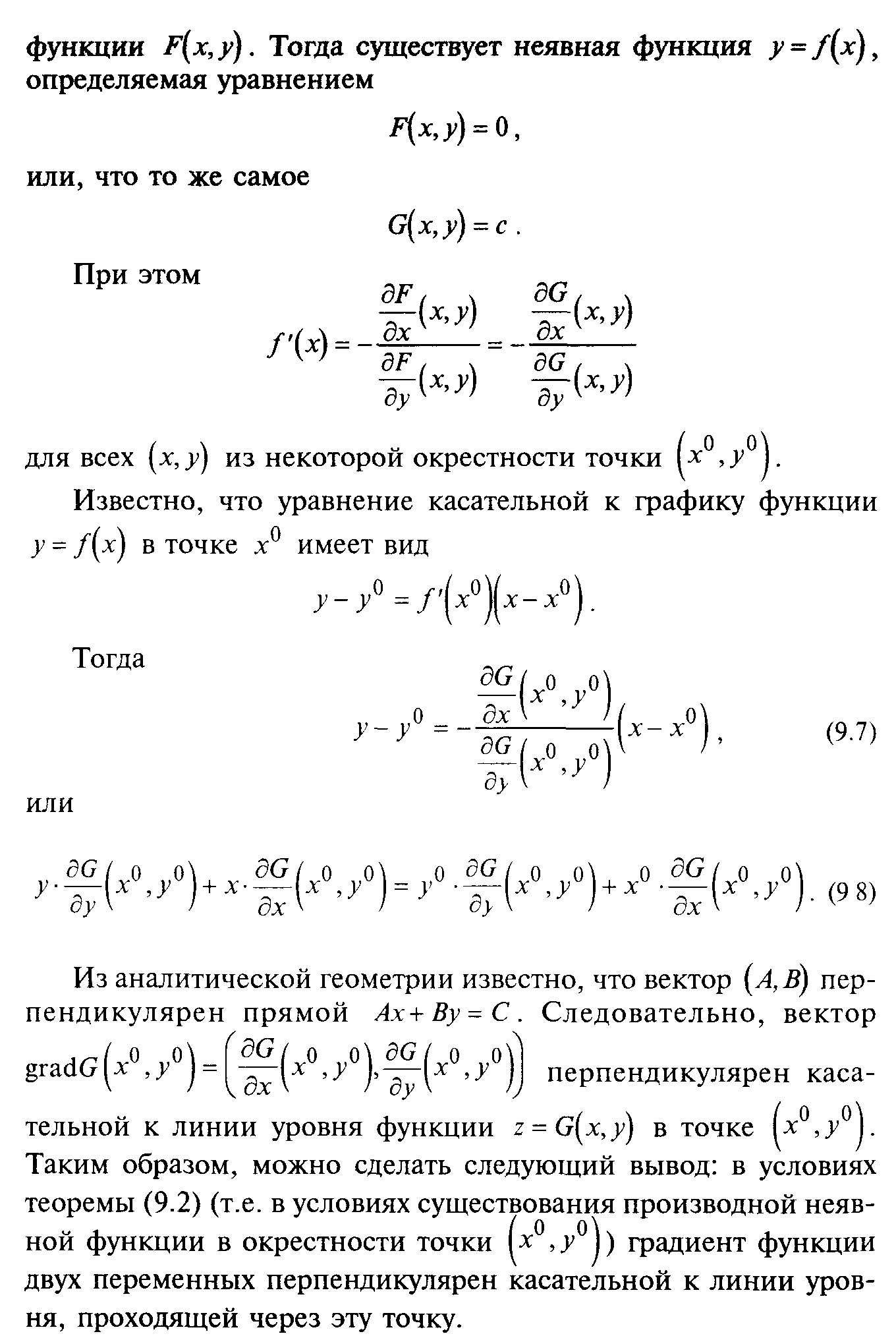
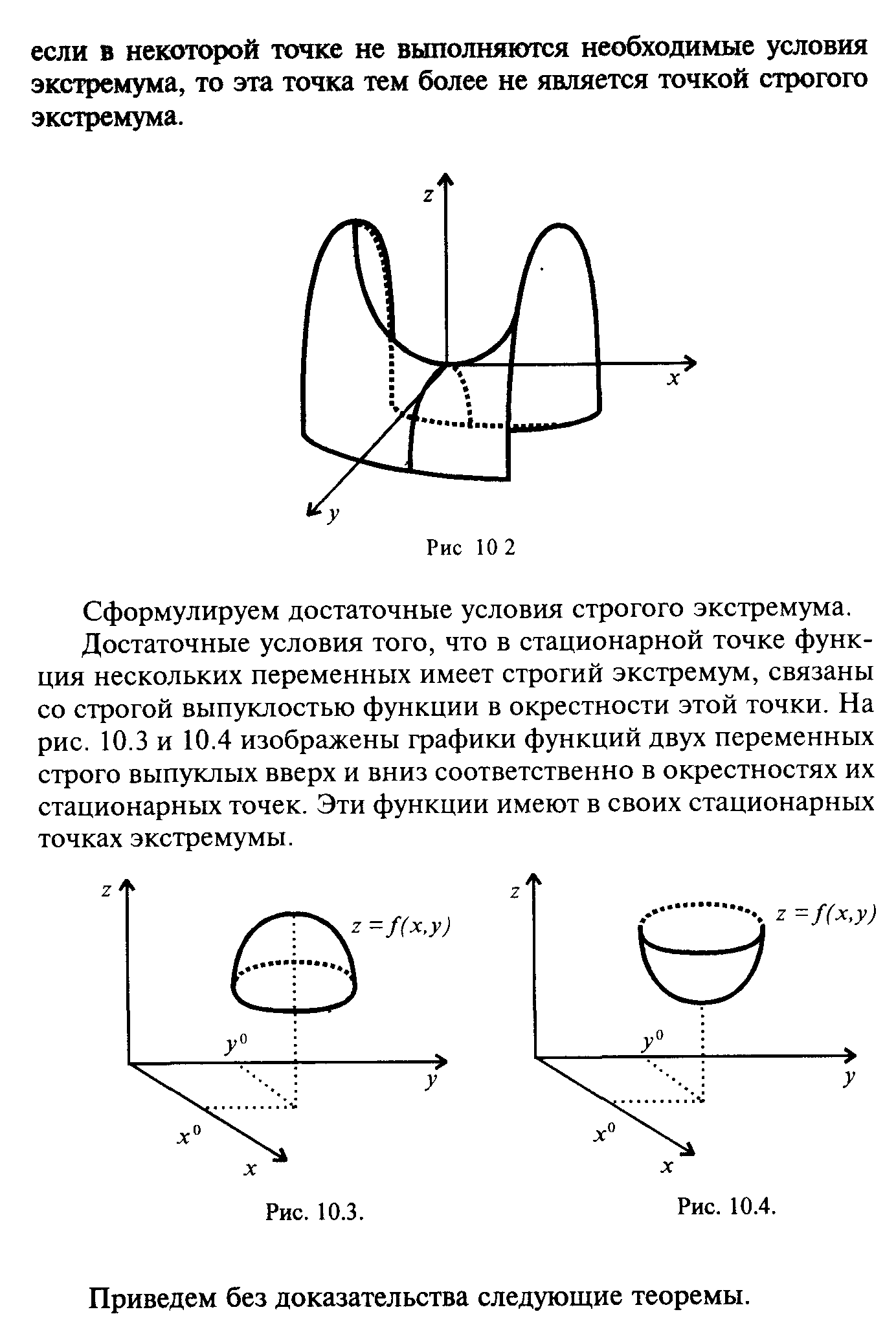
§ 10. Экстремумы функций нескольких переменных

§ 11. Относительный экстремум. Метод Лагранжа

§ 12. Наибольшее и наименьшее значение функции. Метод наименьших квадратов

§ 13. Однородные функции