1. Вычислить , если , , где и – единичные векторы, угол между которыми равен .

2. Даны точки и . Найти , направляющие косинусы вектора , величину проекции вектора на базисный вектор .

3. Найти неизвестную координату вектора , если .

4. Найти угол между векторами и .

5. При каких векторы и ортогональны?

6. Даны вершины четырехугольника , , , . Доказать, что его диагонали и взаимно перпендикулярны.

7. Найти , если , , .

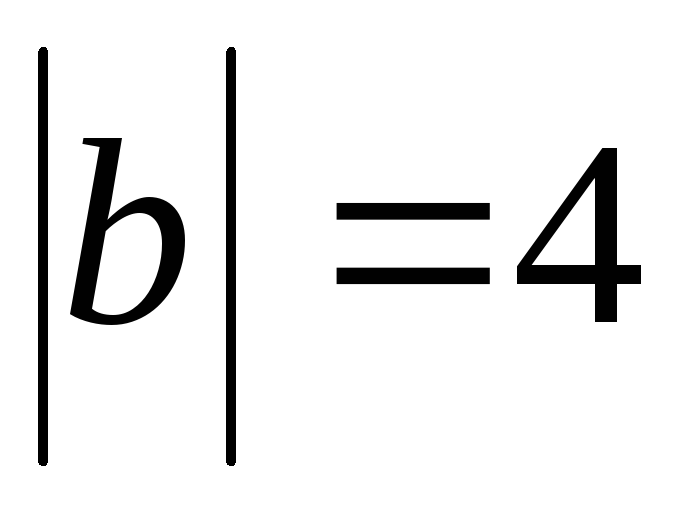8. Доказать, что векторы и ортогональны тогда и только тогда, когда .

9. Даны три силы , и , приложенные в одной точке. Вычислить какую работу производит равнодействующая этих сил, когда точка приложения, двигаясь прямолинейно, перемещается из положения в положение .

1. Контрольные задания

Рекомендуемая литература [1, гл. 1, §2–3], [2, гл. 2, §2.5, 2.6, 2.10–2.12], [3, гл. 1, §1.3, 1.4].

1. Доказать, что векторы и пространства равны тогда и только тогда, когда их координаты равны в любом базисе.

2. Векторы , заданы в некотором базисе пространства. Показать, что векторы образуют базис пространства, и найти координаты вектора в базисе .

1) , , , ;

2) , , , .

3. Найти скалярное произведение векторов (–3+4) и (2+3), где .

4. При каких векторы и ортогональны?

5. Найти вектор , коллинеарный вектору и удовлетворяющий равенству .

6. Даны векторы и . Найти проекцию вектора на вектор .

7. Вычислить работу силы при перемещении материальной точки под действием этой силы из точки в точку вдоль .

3. Векторное произведение векторов. Смешанное произведение векторов

Цель занятия: усвоение понятий векторного и смешанного произведений векторов, выработка навыков вычисления векторного и смешанного произведений и использование их в приложениях.

1. Векторное произведение векторов

   1. Определение. Векторным произведением неколлинеарных векторов и называется вектор, обозначаемый ×, удовлетворяющий следующим требованиям:

1) длина вектора × равна , где , ;

2) вектор × ортогонален обоим векторам и ;

3) тройка векторов , , × является правой.

Если векторы и коллинеарны, то полагают ×=.

При вычислении векторного произведения полезно использовать его свойства. Перечислим их.

2. ×= − ×.

3. ×=, R.

4. ××+×.

5. Если ×=, то векторы , коллинеарны.

6. Длина векторного произведения × равна площади параллелограмма, построенного на векторах и как на сторонах.

Пусть векторы и заданы своими координатами относительно правого ортонормированного базиса , т.е. , . Тогда

×=. (9)

Приложения векторного произведения в механике и физике связаны с понятием момента силы. Моментом силы , приложенной к точке B, относительно некоторой точки А называется векторное произведение .

7. Пример. Заданы векторы , . Найти координаты векторов , .

Решение. Вычисляем координаты вектора по формуле (9):

=.

Координаты вектора определим с помощью свойств векторного произведения векторов. Имеем = =2 (поскольку =0).

8. Пример. Найти площадь параллелограмма, построенного на векторах , если ; .

Решение. Имеем

(поскольку ). Итак (кв. ед.).

2. Смешанное произведение векторов

   1. Определение. Пусть , , – произвольные векторы. Возьмем векторное произведение ×. Далее возьмем скалярное произведение (×) векторов × и . Полученное число называется смешанным произведением векторов , , (в указанном порядке) и обозначается (×)или .

Перечислим основные свойства смешанного произведения.

2. Если векторы , , некомпланарны и образуют правую тройку, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах, как на ребрах, т.е.

(×)=V.

Если же векторы , , некомпланарны и образуют левую тройку, то

(×)=–V.

Векторы , , компланарны тогда и только тогда, когда

(×)=0.

3. (×)=(×)=(×).

Пусть , , заданы в ортонормированном базисе , , , . Тогда

(×)= (10)

Свойство (п.3.2.2) позволяет непосредственно или с помощью формулы (10) вычислять объемы некоторых тел. В частности, объем пирамиды с вершинами в точках , , , выражается следующим образом:

. (11)

Свойство (п.3.2.3) позволяет устанавливать, компланарны или некомпланарны векторы , , . Если векторы , , некомпланарны, то с помощью свойства (п.3.2.2) можно установить, какую тройку они образуют. А именно, если (×)>0, то тройка векторов , , правая, если же (×)<0, то тройка , , левая.

4. Пример. Доказать, что точки А(5, 7, 2), B(3, 1, –1), C(9, 4, –4), D(1, 5, 0) лежат в одной плоскости.

Решение. Найдем координаты векторов: , . Найдем смешанное произведение полученных векторов:

,

Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.

5. Пример. Вычислить объем пирамиды, вершинами которой являются точки , , , .

Решение. Рассмотрим векторы (рисунок 5): , , .

У пирамиды, построенной на векторах , , , та же высота, что и у параллелепипеда, а площадь основания в 2 раза меньше, поэтому

.

Заметим, что векторы , , образуют правую тройку, т.к. (×)>0. Объём пирамиды можно было найти прямо по формуле (11), однако, если нужно найти и другие параметры тела, удобнее начинать решение с построения векторов , , .