1.3. Несвободное твёрдое тело

Твёрдое тело, на перемещение которого не наложено никаких ограничений, называется свободным. Тело, ограничивающее свободу движения данного твёрдого тела, является по отношению к нему связью.

Твёрдое тело, свобода движения которого ограничена связями, называется несвободным. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождаемости твёрдых тел от связей).

Все связи можно разделить на несколько типов.

1. Идеально гладкая поверхность.

Рис. 1.11

Реакции опоры, приложены в точке опоры, всегда направлены перпендикулярно опоре.

2. Гибкая связь (трос, нить, цепь, канат)

Рис. 1.12

Реакция гибкой нити, направлена на нити к точке подвеса.

3. Жёсткий стержень

На схемах показывается толстой линией. Реакция стержня направлена вдоль стержня. Стержень может быть сжат или растянут. Точное направление реакции определяют, мысленно убрав стержень и анализируя направление перемещение узла.

Рис. 1.13

4. Брус.

Рис. 1.14

5. Цилиндрическая шарнирно – неподвижная опора

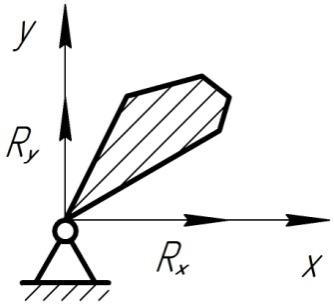
Рис. 1.15

6. Цилиндрическая шарнирно – подвижная опора

Рис. 1.16

7. Защемление (заделка)

Рис. 1.17

8. Невесомый стержень, на концах которого шарниры

Рис. 1.18

9. Сферический шарнир

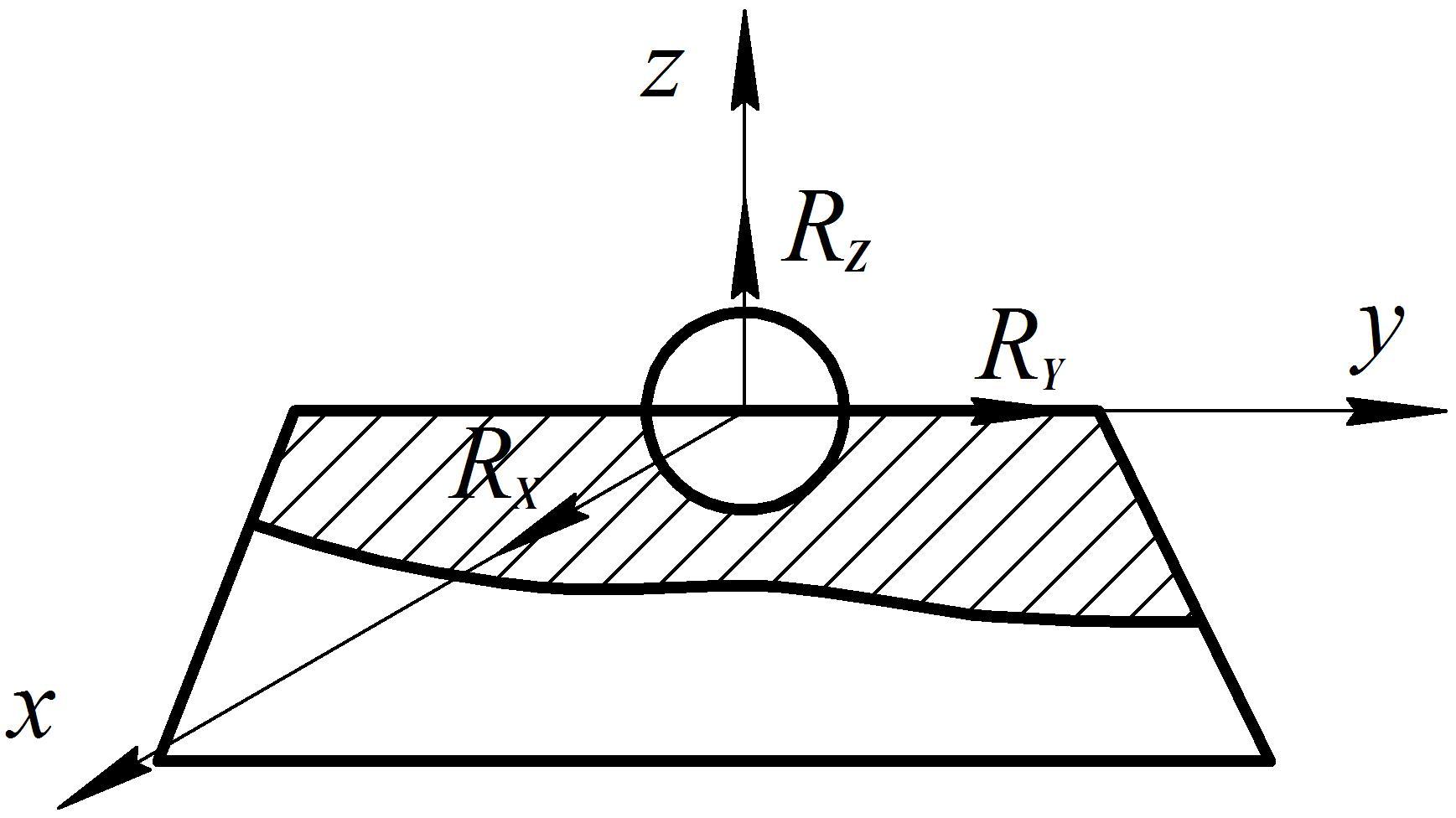
Рис. 1.19

10. Подпятник

(Совокупность цилиндрического шарнира и упорной поверхности)

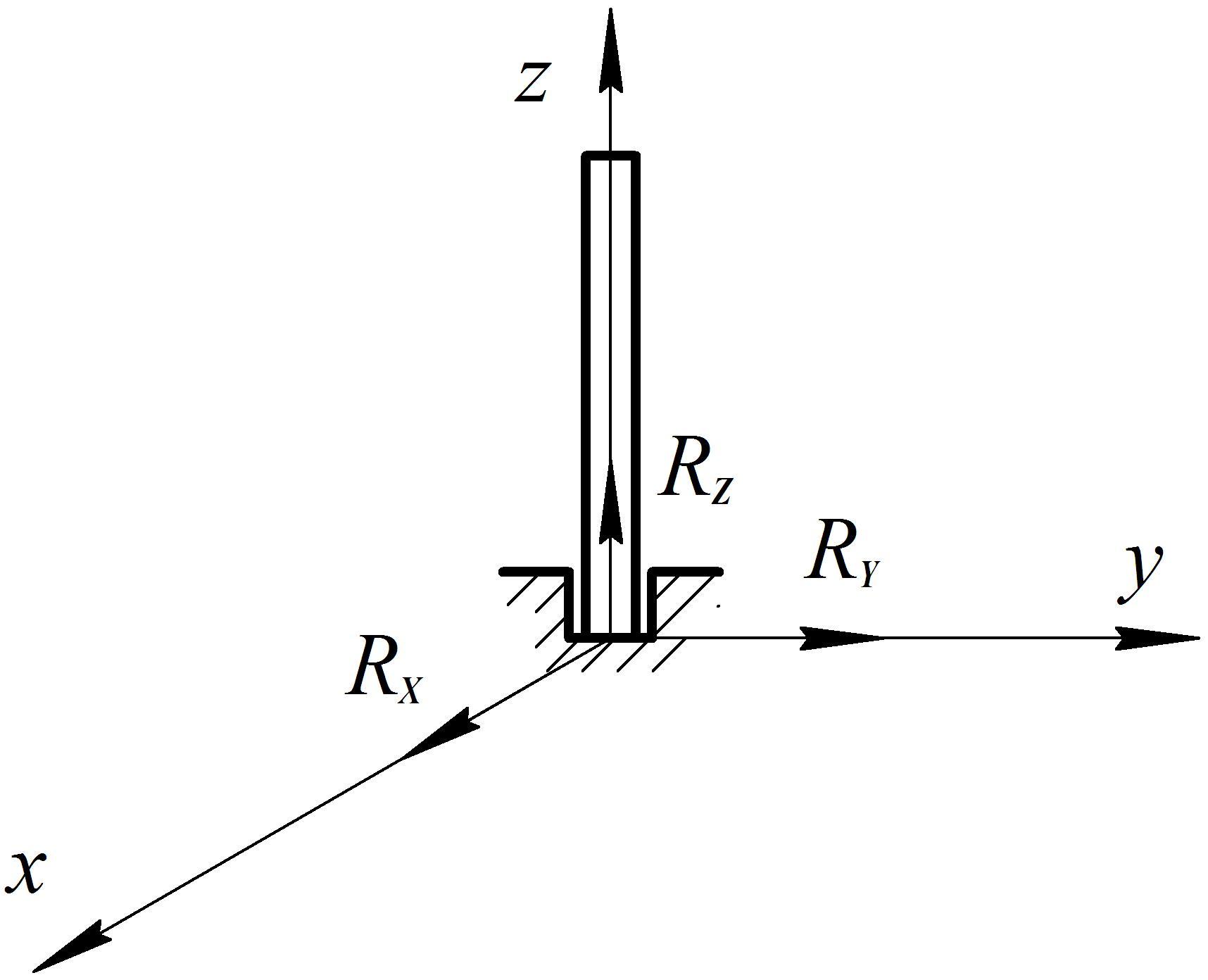
Рис. 1.20

2. Плоская система сил

2.1. Система сходящихся сил

2.1.1 Равновесие твёрдого тела, к которому приложена система сходящихся сил.

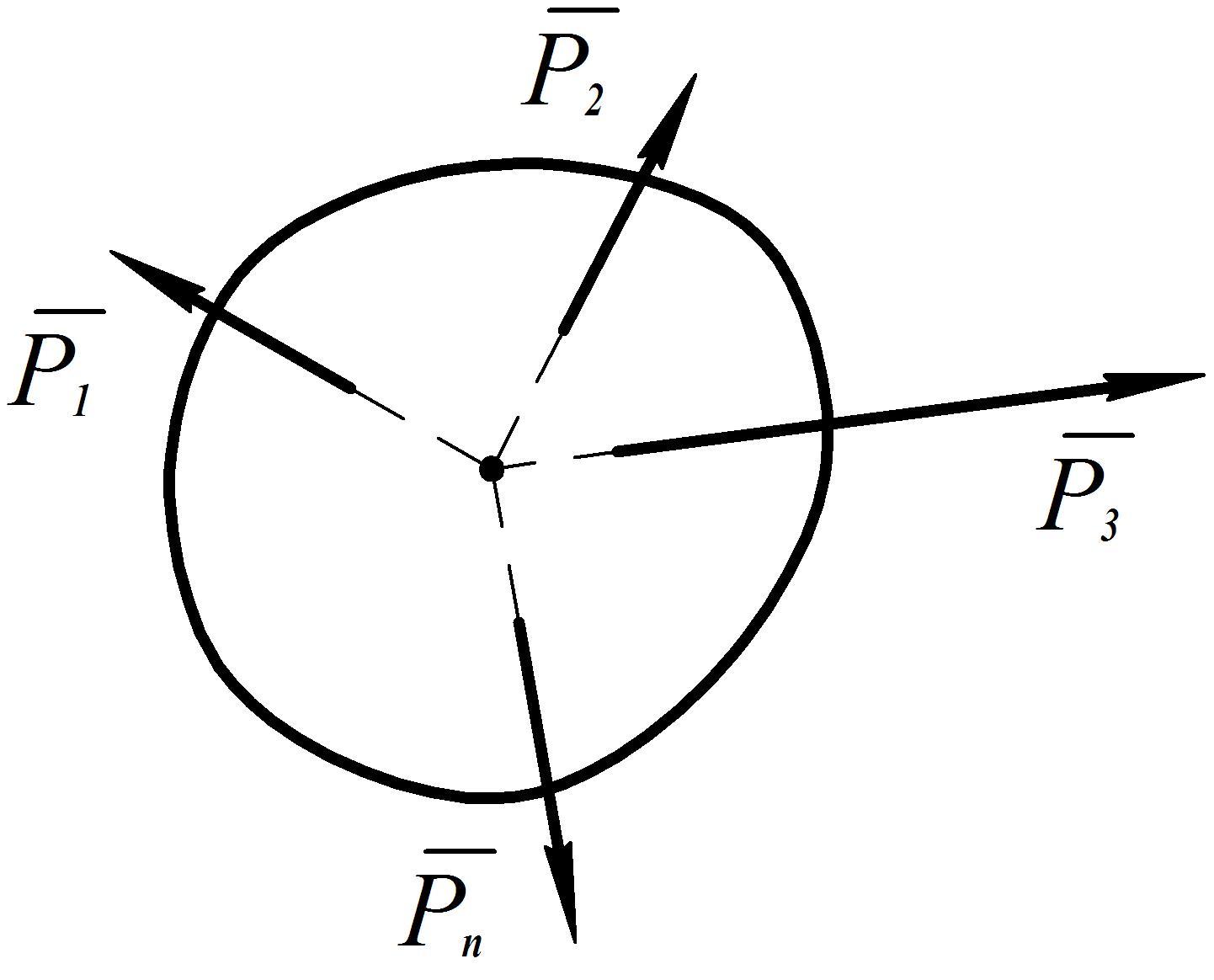
Сходящимися называются силы, линии, действия которых пересекаются в одной точке.

Теорема. Система сходящихся сил эквивалентна общей силе, равнодействующей, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия.

Согласно следствию из аксиомы 3 перенесём точки приложения сил по линиям их действия в точку пересечения этих линий. Она эквивалентна исходной системе сходящихся сил.

Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма (4 аксиома).

Рис. 1.21

(1)

Равнодействующая системы сил приложенных в одной точке, приложенных, в той же точке и изображается замыкающей стороной силового многоугольника.

Рис. 1.22

Строим силовой многоугольник: от конца отложим от его конца и так далее. Затем соединить начало первого вектора с концом последнего. Последний вектор и есть

Рис. 1.23

Обе части (1) спроектируем на оси x, y,z.

(2)

Модуль равнодействующей

(3)

Направление равнодействующей определяется направляющимися косинусами

где i, j, k – единичные орты осей x, y, z.

Для равновесия твёрдого тела, к которому приложена система сходящихся сил, необходимо и достаточно, чтобы векторная сумма этих сил равнялась нулю: (*)

Это означает, что в силовом многоугольнике уравновешенной системе сходящихся сил конец последней силы должен совпадать с началом первой, то есть многоугольник замкнут.

Рис. 1.24

Равенство (*) на основании (3) с учётом (2) выполняется при условии, что

(4)

или

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические проекции всех сил данной системы на координаты осей x, y, z равнялись нулю.

Для плоской системы сходящихся сил система принимает вид:

2.1.2. Теорема о трех не параллельных силах.

Если исходное тело находится в равновесии под действием трех не параллельных сил, лежащих в одной плоскости, то лини действия этих сил пересекаются в одной точке.

Доказательство:

Пусть на тело действует система трех сил , причём линии действия и пересекаются в точке А, согласно аксиоме 4 их можно заменить одной .

Рис. 1.25

Таким образом, рассматриваемая система сил приведена к двум и . По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 2 силы и должны иметь общую линию действия, но тогда линии действия всех трёх сил должны пересекаться в одной точке.

2.1.3. Момент силы относительно точки.

Опыт показывает, что под действием силы твёрдое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется её моментом.

Моментом силы относительно центра называется вектор равный векторному произведению радиуса – вектора точки приложения силы на вектор силы.

(6)

Рис. 1.26

Вектор – момент силы относительно точки О приложен в т. О

Модуль векторного произведения равен площади параллелограмма построенного на векторных сомножителей.

Его модуль равен

,

В общем случае, момент силы относительно центра алгебраически равен взятому со знаком “+” или “-” произведению модуля силы на плечо силы.

Знак “+” выбираем в том случае, если кратчайший поворот силы вокруг данного центра виден происходящим против часовой стрелки.

Рис. 1.27

Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю.

2.1.4. Теорема Вариньона

Теорема Вариньона для системы сходящихся сил гласит: момент относительно точки равнодействующей системы сходящихся сил равен сумме моментов слагаемых сил относительно той же точки:

Удобство данной теоремы заключается в том, что, минуя непосредственное определение равнодействующей, можно вычислить её момент относительно точки, зная моменты всех слагаемых сил относительно той же точки.

Рис. 1.28

– координаты точки А.

где – проекции силы на координатные оси,

x, y – координаты точки В.

Этой формулой рекомендуется пользоваться в тех случаях, когда определение величины h связано с вычислительными трудностями.