17

Лекция 10 Уравнения плоскости и прямой в пространстве

1.Различные виды уравнения плоскости

Пусть некоторая точка; вектор нормали к искомой плоскости P. Напишем уравнение плоскости, проходящей через точку перпендикулярно вектору ( см. рисунок ).

P

Обозначим через текущую точку пространства.

Уравнение плоскости по точке и нормальному вектору

Дано: Очевидно, тогда и только тогда, когда Отсюда получаем уравнение искомой плоскости:

(1)

Перепишем уравнение (1) в другом виде, получим общее уравнение плоскости (2):

Общее уравнение плоскости

(2)

Здесь

Замечание.

Зная общее уравнение плоскости, можно выписать координаты вектора нормали. Они совпадают с коэффициентами при переменных x, y, z.

Примеры. 1. Выпишем уравнение плоскости, проходящей через точку (1,2,3) перпендикулярно вектору :

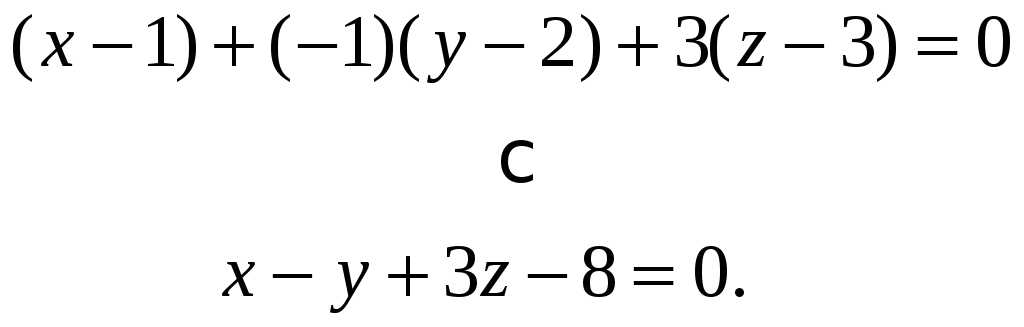
2. Выпишем уравнение нормали к плоскости

Пусть известны координаты трех точек (не лежащих на одной прямой), принадлежащих искомой плоскости Выпишем уравнение плоскости, проходящей через эти три точки .

Обозначим через текущую точку пространства. Очевидно, что эта точка принадлежит плоскости P тогда и только тогда, когда векторы компланарны (см.рисунок):

Запишем условие компланарности трех векторов:

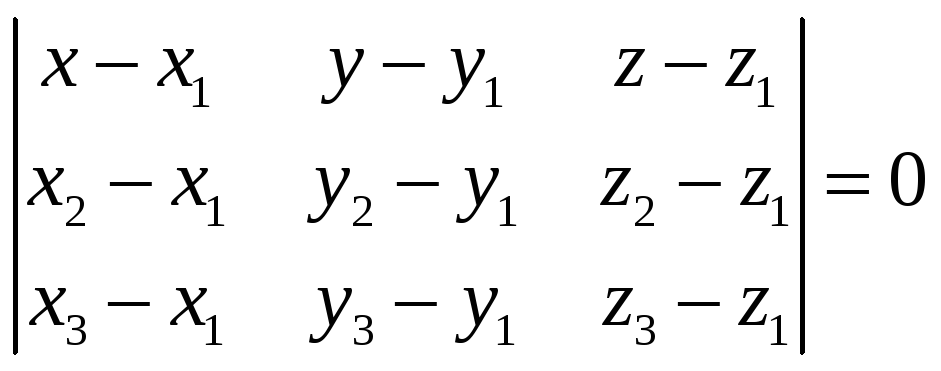
Уравнение плоскости по трем точкам

(3)

Уравнение (3) называется уравнением плоскости по трем точкам.

Пусть некоторая плоскость дана своим общим уравнением:

причем

Перепишем это уравнение в виде

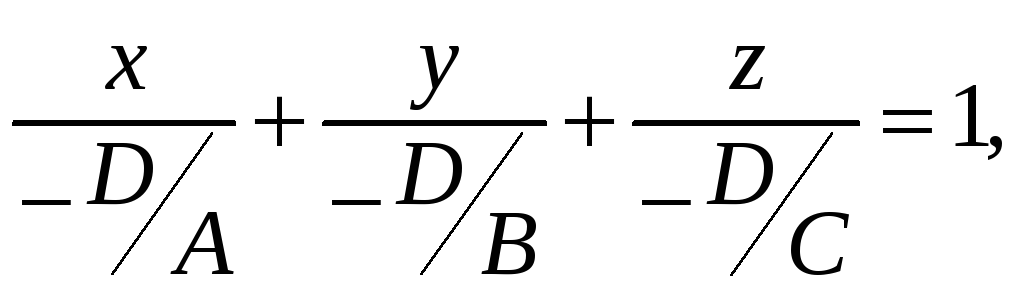
иначе

Уравнение плоскости

«в отрезках»

(4)

Уравнение (4) называется уравнением плоскости «в отрезках». Отметим, что

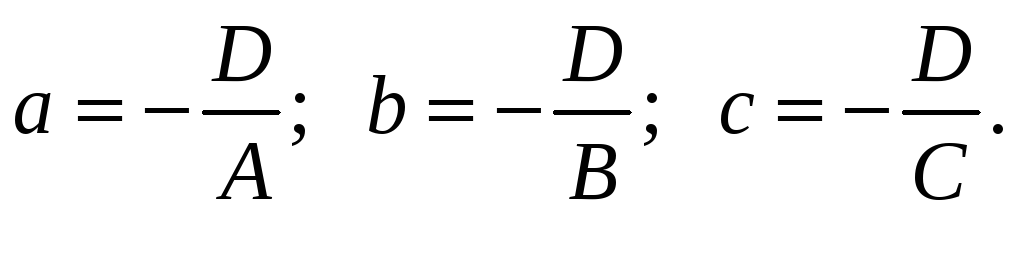
Величины имеют простой геометрический смысл. Их модули равны длинам отрезков, отсекаемых плоскостью от осей координат ( см. рисунок ):

Z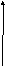

|c|

|b|

Y

|a|

X

Примеры.

1.Выпишем общее уравнение плоскости, проходящей через три точки

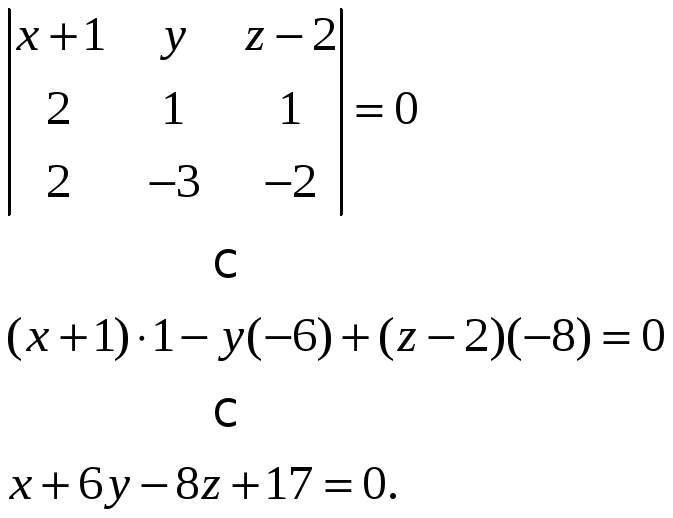
2.Вычислим отрезки, отсекаемые плоскостью от осей координат.

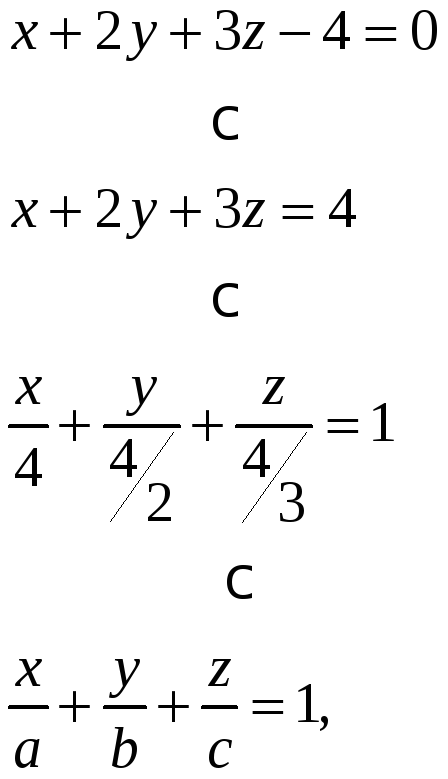
где Длины отрезков равны

Перейдем к составлению нормального уравнения плоскости. Пусть перед нами поставлена следующая задача:

написать уравнение плоскости, удаленной от начала координат на расстояние и имеющей нормальный вектор:

Обозначим через текущую точку пространства. Пусть проекция точки О ( начала координат ) на плоскость P ( см.рисунок );

Z

Q

M

A

O

Y

X

Очевидно, Имеем: Очевидно, что точка M принадлежит плоскости P тогда и только тогда когда

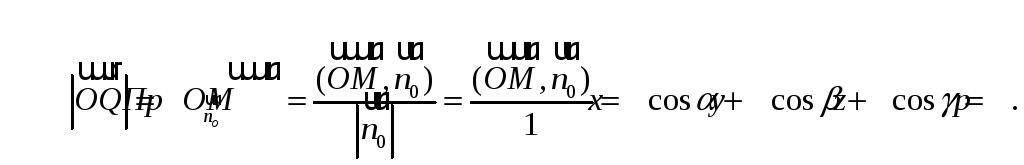
Отсюда получаем:

(

Нормированное уравнение плоскости

5)

Уравнение (5) называется нормированным уравнением плоскости. В нем направляющие косинусы вектора нормали, pрасстояние от начала координат до плоскости P.

Пусть известно нормированное уравнение плоскости (5).

Определение. Величина называется отклонением точки от плоскости P.

Утверждение.

если точки О и М лежат по одну сторону от плоскости P

если точки О и М лежат по разные стороны от плоскости P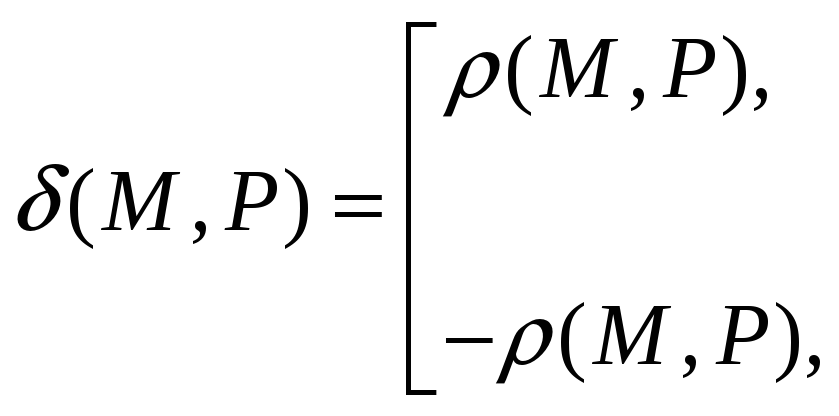

Доказательство. Рассмотрим случай, когда точки М и О лежат по разные стороны от плоскости Р (другой случай рассматривается аналогично).

Z

Q

Y

M

A

Y

O

X

Очевидно, .

Предположим, плоскость P задана своим общим уравнением. Чтобы нормировать уравнение плоскости, умножим обе части общего уравнения плоскости на так называемый нормирующий множитель μ,

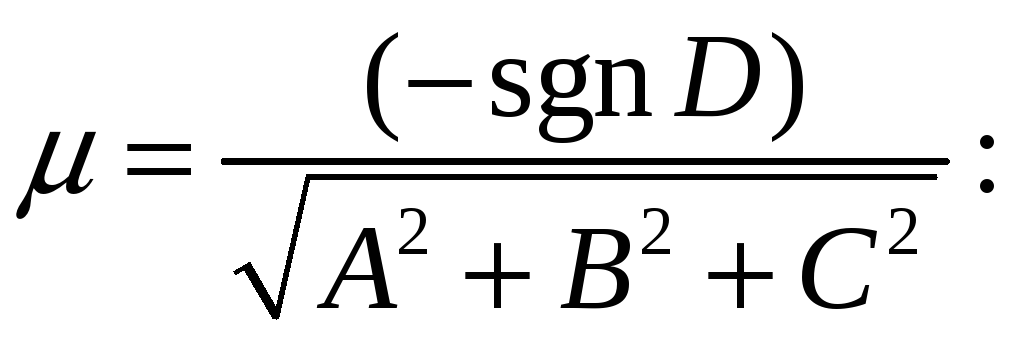
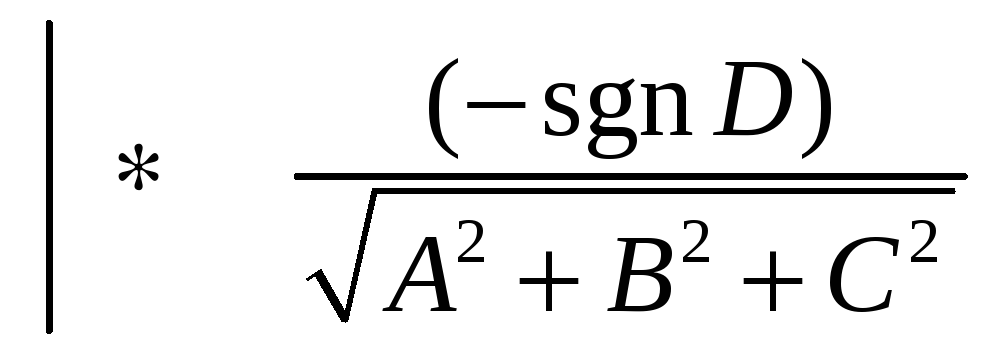
Искомое нормированное уравнение плоскости P

,

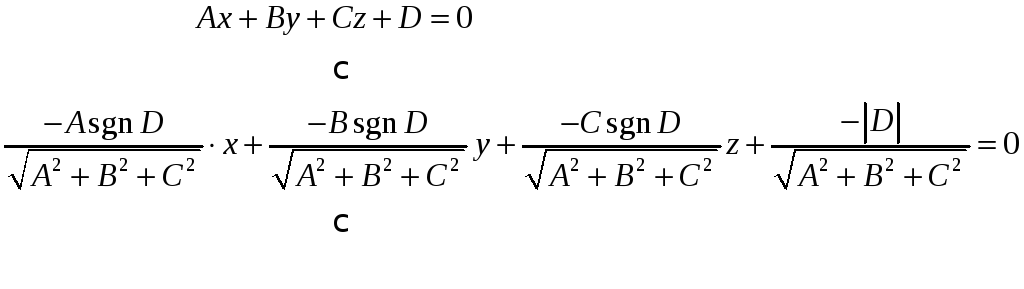
где

.

Примеры.

1.Запишем уравнение плоскости в нормальном виде:

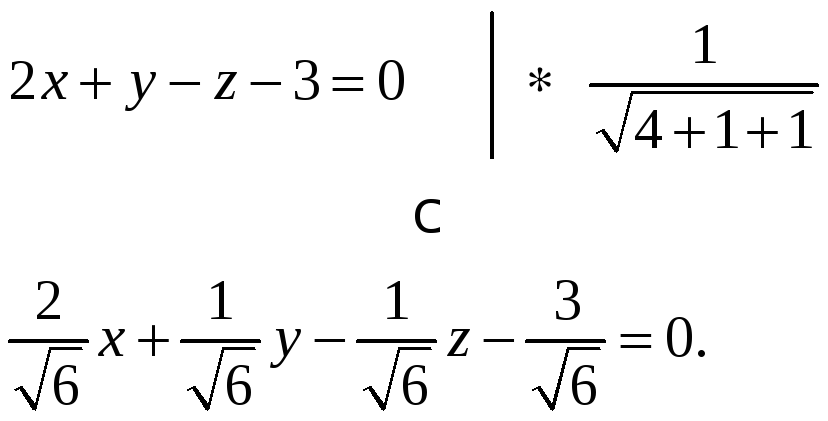
2. Найдём отклонение точки от данной плоскости, а также расстояние от точки до плоскости P.

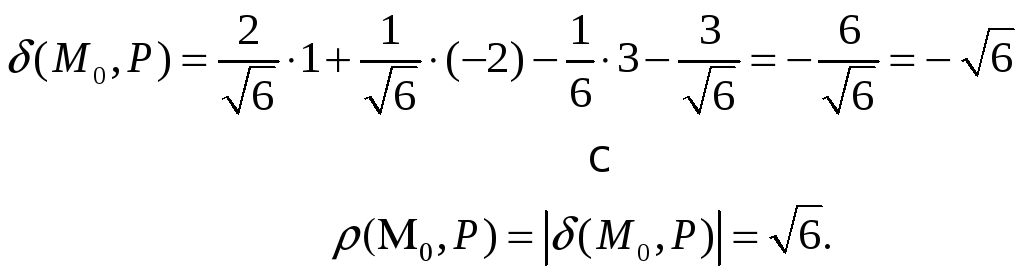
Точки и О лежат по одну сторону от плоскости Р, так как .