
Тема 5 аналіз рядів розподілу методичні вказівки
Ряд розподілу характеризує склад і структуру сукупності за певною ознакою. Він утворюється з двох елементів: варіант — значень групувальної ознаки xj та частот (часток) fj. Співвідношенням варіант і частот подається закономірність розподілу.
Залежно
від статистичної природи варіант ряди
розподілу
поділяються на атрибутивні
та
варіаційні.
Частотними
характеристиками
будь-якого ряду є абсолютна
чисельність j-ї групи
— частота
fj,
відносна
частота j-ї групи — частка dj,
для варіаційних рядів також кумулятивна
частота
![]() — частка
— частка
![]() .
.
Очевидно,
що![]() ,
а
,
а
![]() ,
або 100 %. Кумулятивні характеристики
визначаються послідовним об’єднанням
груп і підсумовуванням відповідних їм
частот (часток).
,
або 100 %. Кумулятивні характеристики
визначаються послідовним об’єднанням
груп і підсумовуванням відповідних їм
частот (часток).
Аналіз закономірностей розподілу ґрунтується на характеристиках: а) центру розподілу; б) варіації; в) форми розподілу (асиметрії, концентрації).
До характеристик центру розподілу відносять середню, моду та медіану. Середня величина характеризує типовий рівень ознаки в сукупності. За даними ряду розподілу середня обчислюється як арифметична зважена, де вагами є частоти fj або частки dj:
 ,
,
![]() ,
,
де j — номер групи; m — кількість груп.
В
інтервальних рядах, припускаючи
рівномірний розподіл елементів сукупності
в межах j-го
інтервалу, за варіанту
![]() беруть середину інтервалу. При цьому
ширину відкритого інтервалу умовно
вважають такою самою, як і сусіднього
закритого інтервалу.
беруть середину інтервалу. При цьому
ширину відкритого інтервалу умовно
вважають такою самою, як і сусіднього
закритого інтервалу.
Модою (Мо) називають найпоширеніше значення ознаки. У дискретному ряді її визначають візуально за найбільшою частотою (часткою). В інтервальному ряді за таким принципом знаходять модальний інтервал, всередині якого конкретне модальне значення обчислюють за інтерполяційною формулою:
![]()
де
![]() та h
— відповідно нижня межа та ширина
модального інтервалу;
та h
— відповідно нижня межа та ширина
модального інтервалу;
![]() — частота (частка) відповідно модального,
передмодального та післямодального
інтервалу.
— частота (частка) відповідно модального,
передмодального та післямодального
інтервалу.
Медіана
(Ме)
— це таке значення ознаки, що варіює,
яке припадає на середину впорядкованого
ряду, поділяючи його на дві рівні
за обсягом частини. Для визначення
медіани використовують кумулятивні
частоти
![]() або частки
або частки
![]() .
У дискретному ряді медіаною є значення
ознаки, кумулятивна частота якої
перевищує половину обсягу сукупності,
тобто
.
У дискретному ряді медіаною є значення
ознаки, кумулятивна частота якої
перевищує половину обсягу сукупності,
тобто
![]() (для кумулятивної частки
(для кумулятивної частки
![]() ).
В інтервальному
ряді за цим принципом визначають
медіанний інтервал, а значення медіани
всередині інтервалу,
як і значення моди, обчислюють за
інтерполяційною формулою:
).
В інтервальному
ряді за цим принципом визначають
медіанний інтервал, а значення медіани
всередині інтервалу,
як і значення моди, обчислюють за
інтерполяційною формулою:
 ,
,
де
![]() та h
— відповідно нижня
межа та ширина медіанного інтервалу;
та h
— відповідно нижня
межа та ширина медіанного інтервалу;
![]() — частота медіанного інтервалу;
— частота медіанного інтервалу;
![]() — кумулятивна частота передмедіанного
інтервалу.
— кумулятивна частота передмедіанного
інтервалу.
У
симетричному розподілі всі три зазначені
характеристики центра розподілу
однакові:
![]() ,
у помірно асиметричному відстань медіани
до середньої втричі менша за відстань
середньої до моди, тобто
,
у помірно асиметричному відстань медіани
до середньої втричі менша за відстань
середньої до моди, тобто
![]() .
.
В одних сукупностях індивідуальні значення ознаки щільно групуються навколо центра розподілу, в інших — значно відхиляються, варіюють. Чим менша варіація, тим однорідніша сукупність, більш надійні й типові характеристики центра розподілу, передусім середня величина. Для вимірювання та оцінювання варіації використовують абсолютні та відносні характеристики.
Найпростішою з таких характеристик є варіаційний розмах R, що характеризує діапазон варіації і визначається як різниця між максимальним і мінімальним значеннями ознаки:
R
=
![]() .
.
Більшість
характеристик варіації визначають,
усереднюючи відхилення індивідуальних
значень ознаки від центра розподілу,
поданого середньою величиною. Оскільки
алгебраїчна сума відхилень дорівнює
нулю (![]() ),
то усереднюються модулі
),
то усереднюються модулі
![]() або квадрати
або квадрати
![]() відхилень. Середній з модулів відхилень
називають середнім
лінійним відхиленням
відхилень. Середній з модулів відхилень
називають середнім
лінійним відхиленням
![]() ,
середній квадрат відхилень — дисперсією
,
середній квадрат відхилень — дисперсією
![]() ,
корінь квадратний з
дисперсії — середнім
квадратичним
відхиленням
,
корінь квадратний з
дисперсії — середнім
квадратичним
відхиленням
![]() :
:
 ;
;
 .
.
За первинними, незгрупованими даними наведені характеристики обчислюють за принципом незваженої середньої:
 або
або
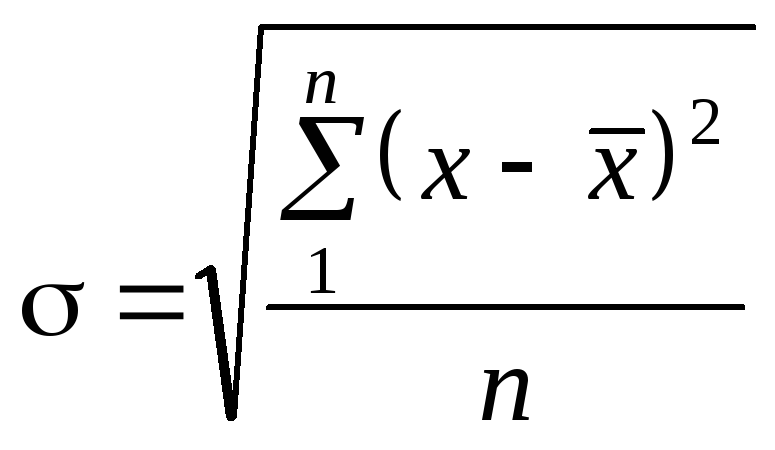 .
.
Середнє
лінійне
![]() та середнє квадратичне
та середнє квадратичне
![]() відхилення — іменовані числа (в одиницях
вимірювання ознаки), за змістом вони
ідентичні, проте згідно з математичними
властивостями
відхилення — іменовані числа (в одиницях
вимірювання ознаки), за змістом вони
ідентичні, проте згідно з математичними
властивостями
![]() >
>
![]() .
.
Дисперсію для ознак метричної шкали обчислюють за формулою:

![]() ,
,
де
![]() —
середній квадрат значень ознаки;
—
середній квадрат значень ознаки;
![]() —
квадрат середньої величини.
—
квадрат середньої величини.
Дисперсія
альтернативної ознаки обчислюється як
добуток часток:
![]() ,
де
,
де
![]() —
частка елементів сукупності, яким
притаманна ознака,
—
частка елементів сукупності, яким
притаманна ознака,
![]() — частка решти елементів
— частка решти елементів
![]() .
.
Порівнюючи
варіації різних ознак або однієї ознаки
в різних сукупностях, використовують
коефіцієнти
варіації
V.
Вони визначаються відношенням абсолютних
іменованих характеристик варіації
(![]() ,
,![]() ,
R)
до центра розподілу і найчастіше
виражаються у процентах. Отже, маємо
коефіцієнти
варіації:
,
R)
до центра розподілу і найчастіше
виражаються у процентах. Отже, маємо
коефіцієнти
варіації:
лінійний
![]() ;
;
квадратичний
![]() ;
;
осциляції
![]() .
.
Аналіз
закономірностей розподілу передбачає
оцінку ступеня однорідності
сукупності та симетричності розподілу.
Критерієм
однорідності
сукупності вважається квадратичний
коефіцієнт
варіації, значення якого в симетричному
розподілі становить
![]() .
.
Найпростішою
мірою
асиметричності
розподілу
є відхилення між характеристиками
центра розподілу. Чим помітніша асиметрія,
тим більше відхилення
![]() .
Стандартизоване відхилення називають
коефіцієнтом
асиметрії
.
Стандартизоване відхилення називають
коефіцієнтом
асиметрії
![]()
![]() .
У разі правосторонньої асиметрії А
>
0, у разі лівосторонньої — А
< 0.
.
У разі правосторонньої асиметрії А
>
0, у разі лівосторонньої — А
< 0.
Оцінка
нерівномірності розподілу між окремими
складовими сукупності (наприклад,
розподілу майна чи доходів між окремими
групами населення) ґрунтується на
порівнянні часток двох
розподілів — за кількістю елементів
сукупності
![]() і обсягом значень ознаки
і обсягом значень ознаки
![]() Якщо розподіл значень ознаки в сукупності
рівномірний, то
Якщо розподіл значень ознаки в сукупності
рівномірний, то
![]() =
=
![]() ,
а відхилення часток свідчать про певну
неоднорідність, яка вимірюється
коефіцієнтами:
,
а відхилення часток свідчать про певну
неоднорідність, яка вимірюється
коефіцієнтами:
локалізації концентрації
Lj
![]() ,
, ![]() .
.
Коефіцієнт локалізації визначається для кожної складової сукупності, коефіцієнт концентрації є узагальнюючою для сукупності характеристикою відхилення розподілу від рівномірного.
Порівняння структур на основі відхилень часток — ефективний спосіб вимірювання диференціації сукупності за даними інтервальних рядів з нерівними інтервалами та атрибутивних рядів. У разі рівномірного розподілу всі значення Lj = 1, а К = 0. Чим помітніша диференціація, тим більше значення цих коефіцієнтів відхиляються, відповідно, від 1 та 0.
Структура
будь-якої статистичної сукупності
динамічна. Зміна
часток окремих складових сукупності
свідчить про структурні зрушення. Мірою
інтенсивності
структурних зрушень
(у
процентних пунктах — п. п.) є середнє
лінійне
![]() або середнє квадратичне
або середнє квадратичне
![]() відхилення часток:
відхилення часток:
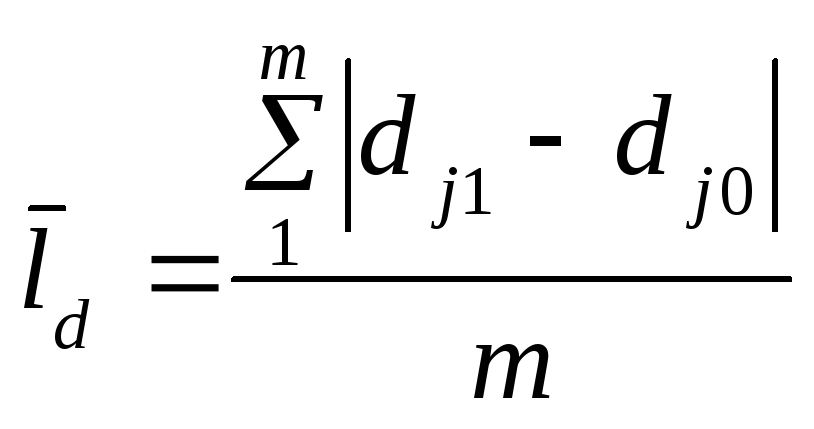 ;
;
![]()
 ,
,
де
![]() та
та
![]() — частки відповідно базисного та
поточного періодів; m
— кількість складових сукупності.
— частки відповідно базисного та
поточного періодів; m
— кількість складових сукупності.
![]() [1,
с. 58—74; 2, с. 64—78; 3, с. 153—163; 184—191; 4,
с.
93—108]
[1,
с. 58—74; 2, с. 64—78; 3, с. 153—163; 184—191; 4,
с.
93—108]
![]()
Кумулятивна частота (частка) характеризує обсяг сукупності зі значеннями варіант, які не перевищують xj.
Абсолютні міри варіації: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії.
Відносні міри варіації: коефіцієнти варіації, локалізації, концентрації.
Однорідна сукупність — це така сукупність, елементи якої мають спільні властивості і належать до одного типу. В однорідних сукупностях розподіли одновершинні (одномодальні).
![]()
-
Як виявляється закономірність розподілу?
-
Назвіть частотні характеристики розподілу і їх особливості.
-
Поясніть сутність характеристик центра розподілу. Як вони співвідносяться?
-
Середня величина ознаки у двох сукупностях однакова. Чи може бути різною варіація цієї ознаки?
-
Поясніть сутність середнього лінійного і середнього квадратичного відхилень. Чи ідентичні вони за змістом і чи однакові за значенням?
-
Як порівняти варіацію різних ознак або однієї ознаки в різних сукупностях?
-
На яких засадах ґрунтується оцінка нерівномірності розподілу? Поясніть зміст і особливості розрахунку коефіцієнтів локалізації та концентрації.
-
Які характеристики варіації застосовують для оцінювання інтенсивності структурних зрушень?
