
- •Содержание
- •Введение
- •Часть 1. Элементы теории множеств и отношений § 1. Понятие множества. Операции над множествами
- •Примеры
- •Операции над множествами
- •Основные тождества алгебры множеств
- •Упражнения
- •§ 2. Декартово произведение двух или нескольких множеств. Понятие отношения. Бинарные отношения
- •Упражнения
- •§ 3. Специальные бинарные отношения. Отношения эквивалентности
- •Упражнения
- •§ 4. Отношения порядка
- •Упражнения
- •§ 5. Функциональные отношения (отображения). Виды отображений
- •Виды отображений:
- •Упражнения
- •Часть 2. Теория графов
- •§ 1. Основные понятия теории графов
- •Способы задания графов. Матричное задание графов.
- •Свойства матриц смежности и инцидентности
- •Упражнения
- •§ Б 2. Булевы матрицы
- •Дизъюнкция (конъюкция)
- •§ 3. Связность графа. Компоненты связности. Матрица связности
- •Выделение компонент связности
- •Алгоритм выделения компонент сильной связности
- •Упражнения
- •§ 4. Полные графы. Двудольные графы. Однородные и реберные графы
- •Упражнения
- •§ 5. Поиск путей (маршрутов) с минимальным числом дуг (ребер)
- •Упражнения
- •§ 6. Расстояние в графах
- •Упражнения
- •§ 7. Нагруженные графы. Расстояния в нагруженном графе
- •Нахождение минимального пути в нагруженном орграфе
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном орграфе из v1 в vi1 (i1≠1)
- •Упражнения
- •§ 8. Эйлеровы цепи и циклы в графах. Эйлеровы графы. Гамильтоновы цепи и циклы в графах. Гамильтоновы графы
- •Упражнения
- •§ 9. Деревья. Остов графа. Цикловой базис графа
- •Алгоритм нахождения кратчайшего остова в нагруженном графе
- •Упражнения
- •§ 10. Раскраска графов. Планарные графы Раскраска вершин графа
- •Одноцветные классы образуют независимые множества вершин.
- •Существуют и приближенные алгоритмы раскрашивания:
- •Упражнения
- •Варианты контрольных работ Часть 1. Элементы теории множеств и отношений Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Часть 2. Теория графов Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Ответы Часть 1
- •Часть 2
- •Тест по теории множеств и отношений
- •Тест по теории графов
- •Библиографический список
- •Любовь Васильевна Архипова Елена Сергеевна Дернович
- •Дискретная математика
§ 3. Связность графа. Компоненты связности. Матрица связности
Определение: Граф (орграф) называется связным (сильно связным), если для любых двух его вершин u,v существует маршрут (путь), соединяющий u,v (из u в v).
Определение: Орграф называется односторонне связным, если для любых двух его вершин по крайне мере одна достижима из другой.
Определение: Псевдографом, ассоциированным с ориентированным псевдографом Д(V, X), называется псевдограф G(V, X0), в котором X0 получается из X заменой всех упорядоченных пар (u,v) на неупорядоченные
Определение: Орграф называется слабо связным, если связным является ассоциированный с ним псевдограф.
Определение: Граф (орграф), не являющийся связным (сильно связным), называется несвязным.
Определение: Компонентой связности (сильной связности) графа, G (орграфа Д), называют его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (орграфа Д).
Количество компонент связности (сильной связности) будем обозначать через p(G) (p(Д))
Определение: Под операцией удаления вершины из графа (орграфа) будем понимать операцию, заключающуюся в удалении некоторой вершины вместе с инцидентными ей ребрами (дугами).
Определение: Вершина графа, удаление которой увеличивает число компонент связности, называется разделяющей (или точкой сочленения).
Утверждение. Если Д’ орграф, полученный в результате удаления нескольких вершин из орграфа Д, то А(Д’) получается из А(Д) в результате удаления строк и столбцов, соответствующих удаленным вершинам.
Замечание. Аналогичное утверждение справедливо и для произвольных псевдографов.
Пусть Д=(V,X) орграф, V={v1,…,vn} – множество вершин.
Определение: Матрицей достижимости орграфа Д называется квадратная матрица T(Д)=[tij] порядка n, у которой
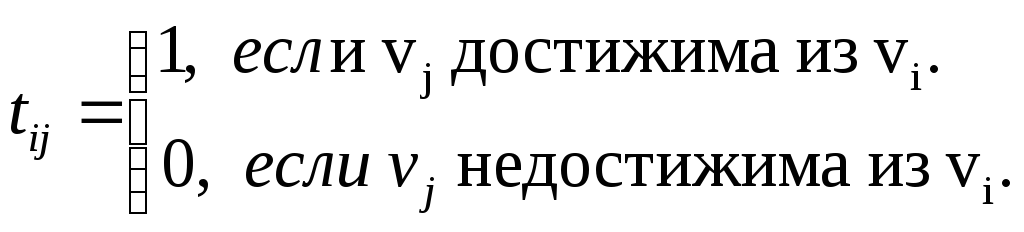
Определение: Матрицей сильной связности орграфа Д называется квадратная матрица S(Д)=[sij] порядка n, у которой
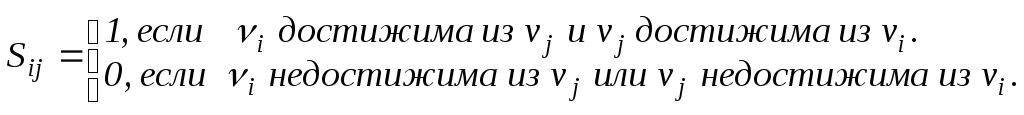
Определение: Матрицей связности графа G называется квадратная матрица S(G)=[sij] порядка n, у которой

Утверждение 1. Пусть дан граф G= (V,X) V={v1,…,vn} Пусть А – матрица смежности. Тогда
S(G)=
sign(E+A+A2+…+An-1)=E![]() A
A![]()
![]()
![]() ….
….![]()
![]()
где Е – единичная матрица порядка n.
Утверждение 2. Пусть дан орграф Д= (V,X) V={v1,…,vn} А – матрица смежности. Тогда
1) Т(Д)=
sign(E+A+A2+…+An-1)=E![]() A
A![]()
![]()
![]() ….
….![]()
![]()
2) S(Д)=
Т(Д)
![]() [Т(Д)]T,
где [Т(Д)]T
– матрица транспонированная Т(Д).
[Т(Д)]T,
где [Т(Д)]T
– матрица транспонированная Т(Д).
Выделение компонент связности
Утверждение
3. Пусть Д орграф, p(Д)
![]() 2 – количество компонент сильной
связности. Д1,…,Др – компоненты
сильной связности. Тогда в результате
удаления из Д вершин, содержащихся в
Д1, получаем орграф с (р-1) компонентами
сильной связности Д2,…,Др.
2 – количество компонент сильной
связности. Д1,…,Др – компоненты
сильной связности. Тогда в результате
удаления из Д вершин, содержащихся в
Д1, получаем орграф с (р-1) компонентами
сильной связности Д2,…,Др.
Утверждение
4. Пусть Д’ компонента сильной связности
орграфа Д.
p(Д)
![]() 2 и Д’’ орграф, полученный удалением
из Д вершин, содержащихся в Д’. Тогда
матрицы A(Д’’), S(Д’’) являются подматрицами
матриц А(Д), S(Д), получаемыми в результате
удаления из них строк и столбцов,
соответствующих вершинам орграфа Д’.
2 и Д’’ орграф, полученный удалением
из Д вершин, содержащихся в Д’. Тогда
матрицы A(Д’’), S(Д’’) являются подматрицами
матриц А(Д), S(Д), получаемыми в результате
удаления из них строк и столбцов,
соответствующих вершинам орграфа Д’.
Утверждение 5. Единицы i-ой строки или i-го столбца матрицы сильной связности орграфа Д=(V, X), V={v1,…,vn}, соответствуют вершинам компоненты сильной связности орграфа Д, содержащей вершину vi.
Из утверждений 3–5 следует алгоритм определения числа компонент сильной связности орграфа Д, а также матриц смежности этих компонент.
