
- •Содержание
- •Введение
- •Часть 1. Элементы теории множеств и отношений § 1. Понятие множества. Операции над множествами
- •Примеры
- •Операции над множествами
- •Основные тождества алгебры множеств
- •Упражнения
- •§ 2. Декартово произведение двух или нескольких множеств. Понятие отношения. Бинарные отношения
- •Упражнения
- •§ 3. Специальные бинарные отношения. Отношения эквивалентности
- •Упражнения
- •§ 4. Отношения порядка
- •Упражнения
- •§ 5. Функциональные отношения (отображения). Виды отображений
- •Виды отображений:
- •Упражнения
- •Часть 2. Теория графов
- •§ 1. Основные понятия теории графов
- •Способы задания графов. Матричное задание графов.
- •Свойства матриц смежности и инцидентности
- •Упражнения
- •§ Б 2. Булевы матрицы
- •Дизъюнкция (конъюкция)
- •§ 3. Связность графа. Компоненты связности. Матрица связности
- •Выделение компонент связности
- •Алгоритм выделения компонент сильной связности
- •Упражнения
- •§ 4. Полные графы. Двудольные графы. Однородные и реберные графы
- •Упражнения
- •§ 5. Поиск путей (маршрутов) с минимальным числом дуг (ребер)
- •Упражнения
- •§ 6. Расстояние в графах
- •Упражнения
- •§ 7. Нагруженные графы. Расстояния в нагруженном графе
- •Нахождение минимального пути в нагруженном орграфе
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном орграфе из v1 в vi1 (i1≠1)
- •Упражнения
- •§ 8. Эйлеровы цепи и циклы в графах. Эйлеровы графы. Гамильтоновы цепи и циклы в графах. Гамильтоновы графы
- •Упражнения
- •§ 9. Деревья. Остов графа. Цикловой базис графа
- •Алгоритм нахождения кратчайшего остова в нагруженном графе
- •Упражнения
- •§ 10. Раскраска графов. Планарные графы Раскраска вершин графа
- •Одноцветные классы образуют независимые множества вершин.
- •Существуют и приближенные алгоритмы раскрашивания:
- •Упражнения
- •Варианты контрольных работ Часть 1. Элементы теории множеств и отношений Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Часть 2. Теория графов Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Ответы Часть 1
- •Часть 2
- •Тест по теории множеств и отношений
- •Тест по теории графов
- •Библиографический список
- •Любовь Васильевна Архипова Елена Сергеевна Дернович
- •Дискретная математика
Часть 2. Теория графов
Исторически сложилось так, что теория графов зародилась в ходе решения головоломок около трехсот лет назад.
Толчок к развитию теория графов получила на рубеже 19 и 20 столетий, когда резко возросло количество работ в области топологии и комбинаторики. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кенига в 30-е годы 20 столетия.
Графы используются в теории планирования и управления, в теории расписаний, в социологии, биологии, химии, медицине, в электронике, теории конечных автоматов и других областях знаний.
§ 1. Основные понятия теории графов
Во многих прикладных задачах изучаются системы связей между различными объектами. Объекты отмечаются точками, а связи между вершинами отмечаются отрезками (стрелками) между соответствующими точками.
Такие системы и образуют графы. Точки – вершины графа. Отрезки – ребра графа.
Граф может изображать сеть улиц в городе: вершины графа – перекрестки, а дуги – улицы с разрешенным направлением движения (улицы могут быть с односторонним и двусторонним движением).
В виде графов можно представить блок-схемы программ (вершины – блоки, а дуги – разрешенные переходы от одного блока к другому), электрические цепи, географические карты, молекулы химических соединений и др.
Определение: Введем в рассмотрение два конечных множества.
V – непустое множество объектов V={v1, …, v n}
X – некоторый набор пар элементов из V вида x=(v, w) (которые связаны между собой)
Графом – называется алгебраическая система G= (V, X), где V – множество вершин графа, а X – множество ребер графа.
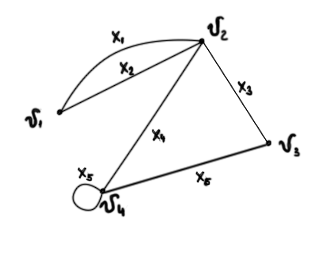
Пример:
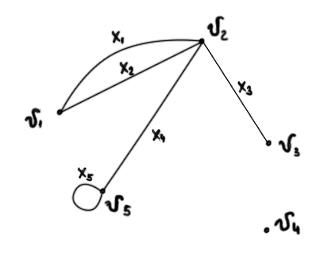
G= (V, X)
V={v1, v2, v3, v4, v5}
X={( v1, v2), (v1, v2), (v2, v3), (v2, v5), (v5, v5)}
или
X={x1, x2, x3, x4, x5}
Определение: Ребра вида (v, v) называются петлями.
Определение: Одинаковые ребра, т.е. соединяющие одни и те же вершины, называются кратными (или параллельными) ребрами.
Определение: Количество кратных ребер (u, v) называется кратностью ребра (u, v).
Определение: Псевдограф – граф с кратными ребрами и петлями.
Определение: Мультиграф – псевдограф без петель.
Определение: Вершины, не принадлежащие ни одному ребру, называются изолированными.
Определение: Если в графе G указано направление ребер, то граф называется ориентированным.
Для ориентированных графов будем использовать букву Д.
Ребра ориентированного графа называются дугами.
Определение: Если направление ребер не указано, то граф называется неориентированным (н-графом) или просто графом.
Если некоторому графу поставлена соответствующая геометрическая конфигурация, то данная конфигурация называется изображением (или реализацией) графа.
Определение: Если x= (u, v) – ребро графа, то вершины u и v называются концами ребра x.
Определение: Если x= (u, v) – дуга орграфа, то u называется началом, а v концом дуги x.
В этом случае говорят: что дуга x исходит из вершины u и заходит в вершину v.
Определение:
Вершины u, v
графа G=(V, X) (орграфа
Д=(V, X)) называются смежными,
если (u, v)![]() Х,
т. е. вершины u, v
называются
смежными, если существует ребро (дуга),
соединяющая их.
Х,
т. е. вершины u, v
называются
смежными, если существует ребро (дуга),
соединяющая их.
Определение: Два ребра называются смежными, если они имеют общую вершину.
Определение: Если вершина v является концом (началом или концом) ребра (дуги) x, то говорят, что вершина v и ребро (дуга) x инциденты.
Определение: Вершина, инцидентная ровно одному ребру, и само ребро называются концевыми (или висячими).
Определение:
Степенью
вершины v
графа G называется
число
![]() v),
равное числу ребер, инцидентных вершине
v.
v),
равное числу ребер, инцидентных вершине
v.
У
изолированной вершины
![]() v)
= 0.
v)
= 0.
У
висячей вершины
![]() v)
= 1.
v)
= 1.
Определение:
Полустепенью
исхода
вершины v
в орграфе Д называется
число
![]() v),
равное количеству дуг, исходящих из
вершины v.
v),
равное количеству дуг, исходящих из
вершины v.
Определение:
Полустепенью
захода
вершины v
в орграфе Д называется число
![]() v),
равное количеству дуг,
заходящих в вершину v.
v),
равное количеству дуг,
заходящих в вершину v.
Кол-во вершин и ребер в графе G будем обозначать соответственно n(G) и m(G). Кол-во вершин и дуг в орграфе Д будем обозначать соответственно n(Д) и m(Д).
Утверждение 1. Для любого псевдографа G выполняется равенство:
![]() .
.
Утверждение 2. Для любого ориентированного псевдографа Д выполняется равенство:
![]() .
.
Определение: Подграфом графа G называется граф, все вершины и рёбра которого содержатся среди вершин и ребер графа G.
Определение: Подграф называется собственным, если он отличен от самого графа.
Определение:
Объединением
графов G1=(V1,
X1)
и G2=(V2,
X2)
называется граф G=G1+G2=(V1![]() V2,
X1
V2,
X1![]() X2).
X2).
Определение:
Пересечением графов G1=(V1,
X1)
и G2=(V2,
X2),
где V1![]() V2
V2
![]() 0,
называется граф G=G1
0,
называется граф G=G1![]() G2=(V1
G2=(V1![]() V2,
X1
V2,
X1
![]() X2).
X2).
Определение: Произведением графов G1=(V1, X1) и G2=(V2, X2) называется граф G=G1×G2=(V, X), для которого V=V1×V2 – декартово произведение множеств вершин исходных графов, а множество ребер X определяется следующим образом: вершины (u1, u 2) и (v1, v2) смежны в графе G тогда и только тогда, когда или u1=v1, а u2 и v2 смежны в графе G2, или u2=v2, а u1 и v1 смежны в графе G1.
Часто бывает важно определить, какие графы считаются различными, а какие не различаются. Обычно это связывают с понятием изоморфизма графов.
Определение: Два графа G1=(V1, X1) и G2=(V2, X2) называются изоморфными, если существуют взаимно однозначные отображения f и g, такие, что f: V1 V2 и g: X1 X2, сохраняющие инцидентность.
Обозначаются: G1 ~ G2.
В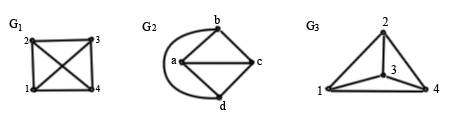 о
многих случаях можно рассматривать
графы с точностью до изоморфизма, т.е.
не различать изоморфные графы. Однако,
если какие-то вершины или рёбра графа
обладают различной индивидуальностью,
например, они занумерованы или им
сопоставлены какие-либо численные
характеристики (вес ребра, длина ребра
и др.), то естественно при сравнении двух
графов эту индивидуальность учитывать.
о
многих случаях можно рассматривать
графы с точностью до изоморфизма, т.е.
не различать изоморфные графы. Однако,
если какие-то вершины или рёбра графа
обладают различной индивидуальностью,
например, они занумерованы или им
сопоставлены какие-либо численные
характеристики (вес ребра, длина ребра
и др.), то естественно при сравнении двух
графов эту индивидуальность учитывать.
G1~G2~G3
Определение:
Последовательность вершин и ребер (дуг)
графа G (орграфа Д) v1x1v2x2v3…xkvk+1(k![]() 1)
называется маршрутом
(путём)
из вершины v1
в вершину vk+1.
1)
называется маршрутом
(путём)
из вершины v1
в вершину vk+1.
Определение: Длина пути (маршрута) равна количеству дуг (ребер) в последовательности (=k).
Определение: Вершина v1 называется началом маршрута (пути), а vk+1 – концом. Остальные вершины называются внутренними.
Маршрут (путь) рассматривается как непрерывная траектория движения по вершинам и рёбрам графа.
Пример: v1x1v2x3v3x6v4 – маршрут из v1 в v4 длиной 3.
Определение: Незамкнутый маршрут (путь), в котором все рёбра (дуги) попарно различны, называется цепью.
Определение: Цепь, в которой все вершины попарно различны, называется простой цепью.
Определение: Замкнутый маршрут (путь), в котором все ребра (дуги) попарно различны, называется циклом (контуром).
Определение: Цикл (контур), в котором все вершины попарно различны, называется простым циклом (простым контуром).
Определение: Неориентированный граф без циклов называется ациклическим.
Определение: Орграф, не имеющий контуров, называется бесконтурным.
Определение: Вершина v называется достижимой из вершины u, если существует маршрут, связывающий вершины u и v.
