- •Содержание
- •Введение
- •Часть 1. Элементы теории множеств и отношений § 1. Понятие множества. Операции над множествами
- •Примеры
- •Операции над множествами
- •Основные тождества алгебры множеств
- •Упражнения
- •§ 2. Декартово произведение двух или нескольких множеств. Понятие отношения. Бинарные отношения
- •Упражнения
- •§ 3. Специальные бинарные отношения. Отношения эквивалентности
- •Упражнения
- •§ 4. Отношения порядка
- •Упражнения
- •§ 5. Функциональные отношения (отображения). Виды отображений
- •Виды отображений:
- •Упражнения
- •Часть 2. Теория графов
- •§ 1. Основные понятия теории графов
- •Способы задания графов. Матричное задание графов.
- •Свойства матриц смежности и инцидентности
- •Упражнения
- •§ Б 2. Булевы матрицы
- •Дизъюнкция (конъюкция)
- •§ 3. Связность графа. Компоненты связности. Матрица связности
- •Выделение компонент связности
- •Алгоритм выделения компонент сильной связности
- •Упражнения
- •§ 4. Полные графы. Двудольные графы. Однородные и реберные графы
- •Упражнения
- •§ 5. Поиск путей (маршрутов) с минимальным числом дуг (ребер)
- •Упражнения
- •§ 6. Расстояние в графах
- •Упражнения
- •§ 7. Нагруженные графы. Расстояния в нагруженном графе
- •Нахождение минимального пути в нагруженном орграфе
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном орграфе из v1 в vi1 (i1≠1)
- •Упражнения
- •§ 8. Эйлеровы цепи и циклы в графах. Эйлеровы графы. Гамильтоновы цепи и циклы в графах. Гамильтоновы графы
- •Упражнения
- •§ 9. Деревья. Остов графа. Цикловой базис графа
- •Алгоритм нахождения кратчайшего остова в нагруженном графе
- •Упражнения
- •§ 10. Раскраска графов. Планарные графы Раскраска вершин графа
- •Одноцветные классы образуют независимые множества вершин.
- •Существуют и приближенные алгоритмы раскрашивания:
- •Упражнения
- •Варианты контрольных работ Часть 1. Элементы теории множеств и отношений Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Часть 2. Теория графов Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Ответы Часть 1
- •Часть 2
- •Тест по теории множеств и отношений
- •Тест по теории графов
- •Библиографический список
- •Любовь Васильевна Архипова Елена Сергеевна Дернович
- •Дискретная математика
Примеры


![]()
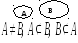
Операции над множествами
-
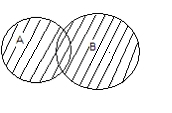
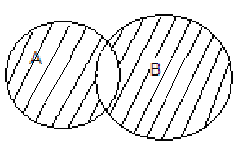
Объединение (сумма) множеств A и B обозначается
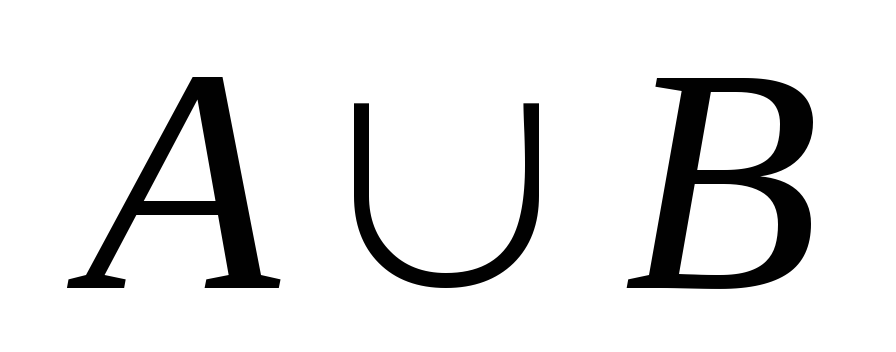 :
:
![]()
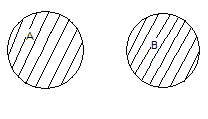
-
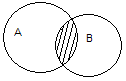
Пересечение (произведение) множеств A и B обозначается
 :
:
![]()
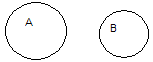
![]()
-
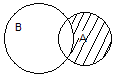
Разность множеств A и B (относительное дополнение множества B до множества A) обозначается
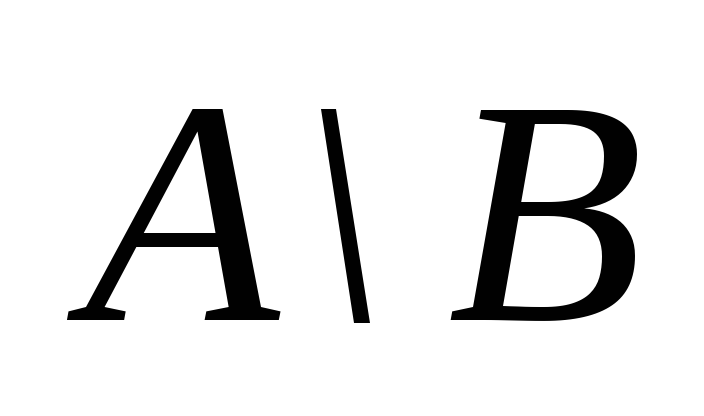 :
:
![]()
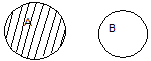
-
Отрицание множества A (абсолютное дополнение множества A) обозначается
 :
:
![]()

-
Симметрическая разность множеств A и B обозначается
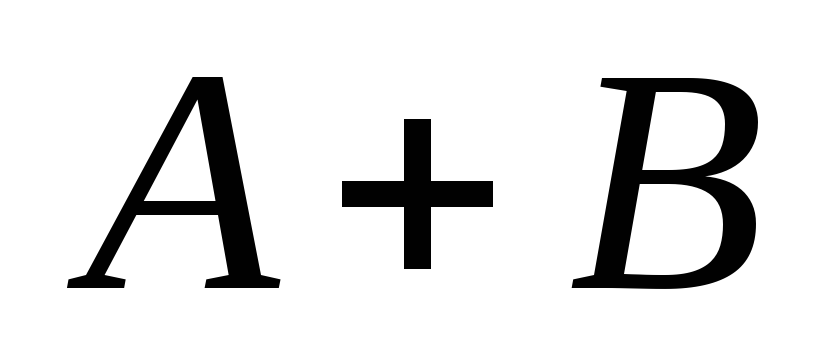 :
:
![]()
Основные тождества алгебры множеств
1.
![]() 1´.
1´.
![]()
идемпотентность
2.
![]() 2´.
2´.
![]()
коммутативность
3.
![]() 3´.
3´.
![]()
ассоциативность
дистрибутивность
5.
![]() 5´.
5´.
![]()
6.
![]() 6´.
6´.
![]()
7.
![]() 7´.
7´.
![]()
8.
![]() 8´.
8´.
![]()
законы де Моргана
9.
![]() 9´.
9´.
![]()
законы поглощения
10.
![]() 10´.
10´.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
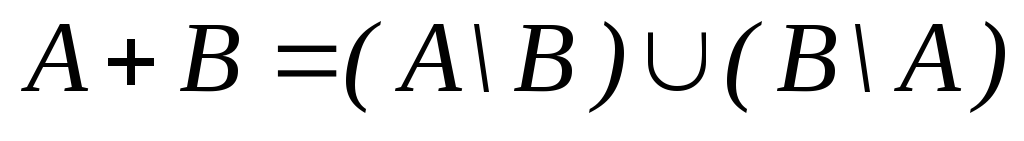
Упражнения
1.1. Принадлежат ли числа 1, 3 следующим множествам: А1=1, А2=1, А3=1, 2, А4=2, -1, А5=1, 2, А6=х | х=3k, kZ, А7=x / х2-1=0, хQ.
1.2. Определить, является ли одно из следующих множеств А1, А2 собственным подмножеством другого:
а) А1=1, 2 А2=1, 2
б) А1=ромбы А2= параллелограммы
в) А1=1 А2=1, 1, 2
г) А1= 1, 2, 1 А2= 2, 1, 1, 1, 1
д) А1=Иванов и родственники Иванова; А2=Иванов, отец Иванова.
е) А1=правильные многоугольники; А2=квадраты.
1.3. Указать множество всех подмножеств множества А:
а) А=1, 2 б) А= , ,
1.4. Вывести формулу для количества подмножеств n-элементного множества.Сколько различных подмножеств имеет множество, состоящее из десяти элементов?
1.5. Найти АВ, АВ, А\В, А+В, В\А, если:
а) А=0;8 В=-5;1
б) А=(-;5 В=0;+)
в) А=х | х=2k, kN В=х | хN
г) А= х | х2+5х+6=0, хR В=х | х3+5х2+6х=0, хR
1.6. Найти множество
А\(![]() С),
если А=(-1;+), В=(-;1),
С=3;+).
С),
если А=(-1;+), В=(-;1),
С=3;+).
1.7. Изобразить на кругах Эйлера-Венна следующие множества:
![]() , (А\В)\С, (А\С)\В,
(А+В)С.
, (А\В)\С, (А\С)\В,
(А+В)С.
1.8. Записать множества, изображенные на кругах Эйлера-Венна:
а) б)
U



А В В U


А
в А


 )
г)
)
г)
В С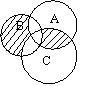

1.9. Из 220 школьников 163 играют в баскетбол, 173 – в футбол, 24 не играют в эти игры. Сколько человек играют одновременно и в баскетбол и в футбол?
1.10. Каждый студент группы обладает хотя бы одним из признаков: юноша, волосы крашеные, получает стипендию. Юношей в группе 12, из них 3 покрасили волосы, а 8 получают стипендию. Всего в группе 6 студентов с крашеными волосами, из них 2 получают стипендию и 1 из двоих – юноша. Стипендию получают 14 человек, из них 8 – юношей. Сколько студентов в группе?
1.11. В диско-клубе собрались представители двух молодежных организаций: комсомола и «Яблоко». Комсомольцев было 24, юношей – 16. Причем юношей-комсомольцев было столько же, сколько девушек – «яблочниц». Сколько человек было на встрече?
1.12. Множество М состоит из m лиц, владеющих хотя бы одним иностранным языком – английским, французским или немецким. Известно, что английским языком владеют 70 лиц, французским – 65, немецким – 50, английским и французским – 40, английским и немецким – 30, французским и немецким – 20, а всеми тремя языками – 5 лиц. Найти m.
1.13. Упростить запись множества, используя основные равенства алгебры множеств:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
1.14. Доказать тождества и показать их верность на кругах Эйлера-Венна:
а)
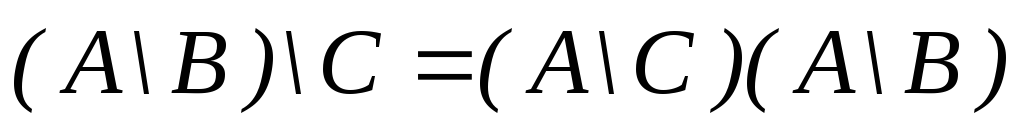
б)
![]()
в)
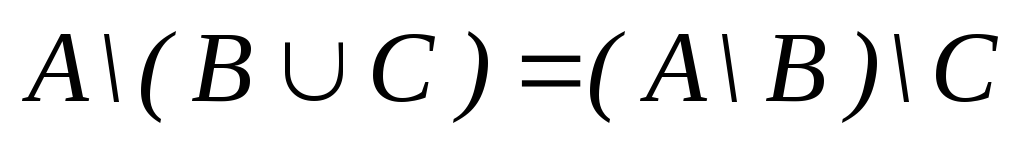
г)
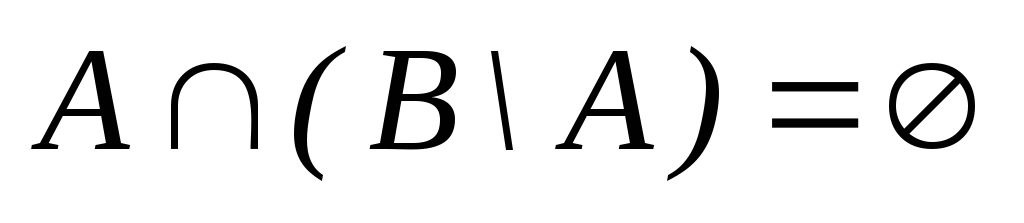
д)