3.3 Перестановки n-ой степени

Пусть – конечное множество, состоящее из элементов. Поскольку в дальнейшем природа элементов этого множества для нас значения не имеет, будем считать, что . Через обозначим множество всех взаимнооднозначных отображений множества в себя. Элементы этого множества называются перестановками -ой степени.

Пусть . В развернутой форме отображение записывается как

,

или

с указанием всех образов , представляющих собой переставленные символы , откуда и идёт название перестановка. В связи с этим перестановку обычно изображают таблицей

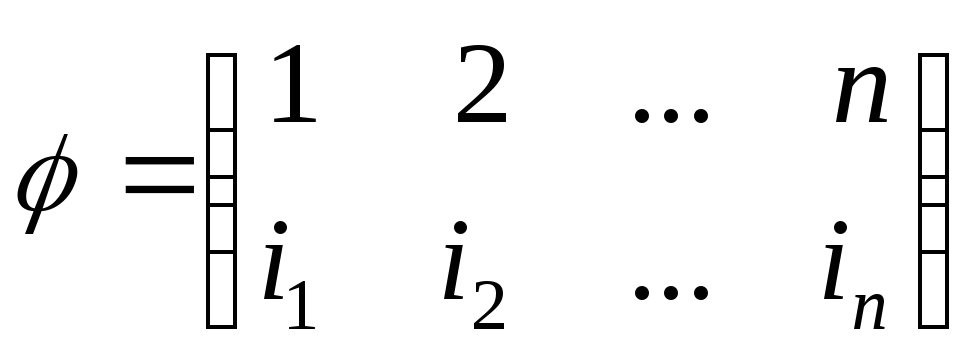, (3.7)

где . В верхнем ряду таблицы (3.7) числа не обязательно должны стоять в порядке возрастания слева - направо. Важно, чтобы под символами верхнего ряда стояли их образы при отображении .

Например,

. (3.8)

В связи с этим перестановку из будем иногда записывать в виде

, (3.9)

где – произвольным образом переставленные символы , а запись перестановки в виде (3.7) будем называть канонической.

Перестановка

является обратной к перестановке вида (3.9) и обозначается .

Например, если имеет вид (3.8),

.

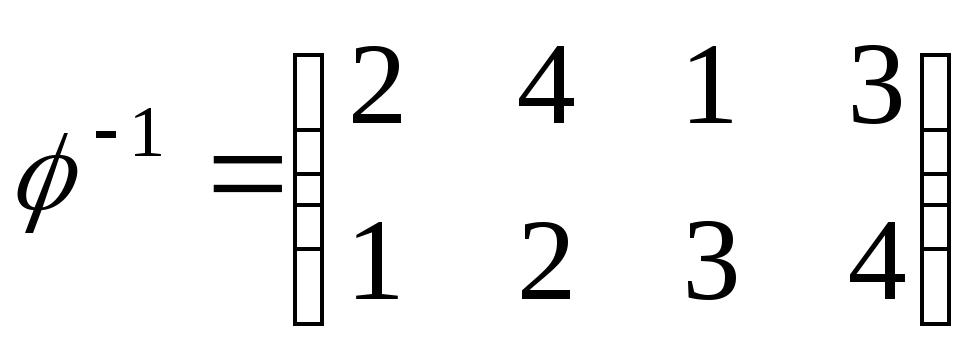Операция умножения перестановок -ой степени вводится как композиция отображений,

.

Например, если

,

то

.

Множество замкнуто относительно операции композиции отображений, т.е. произведение перестановок -ой степени является перестановкой -ой степени. Действительно, композиция обратимых отображений и является обратимым отображением и , т.к.

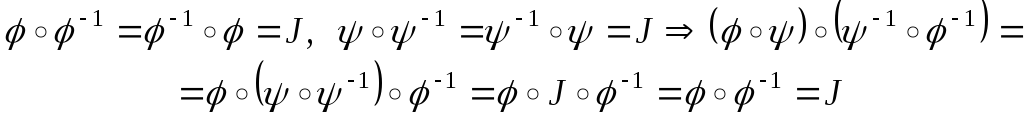
и аналогично .

Но тогда по критерию обратимости отображения (см.п.3.2) –биективное отображение, т.е. перестановка -ой степени.

Множество содержит тождественное отображение, которое обозначается буквой , ,

и называется единичной перестановкой. Очевидно, что для всех

из , т.е. играет роль единицы для операции умножения перестановок. Учитывая, что , причем

,

получаем, что множество перестановок -ой степени по операции умножения перестановок образует группу.

Покажем, что , т.е. число различных перестановок -ой степени равно . При построении перестановки вида (3.7) элемент вида можно выбрать способами, тогда для выбора элемента остаётся возможность, а пара {} может быть выбрана способами. Для выбора элемента остаётся возможности, а тройка {} может быть выбрана способами. Продолжая этот процесс, получаем, что набор {} из различных элементов множества может быть выбран

способами. После этого последний элемент выбирается автоматически как единственный оставшийся элемент множества . Таким образом .

3.4 Четные и нечетные перестановки

Перестановка -ой степени называется циклической, если её можно представит в виде

. (3.10)

Относительно элементов будем говорить, что они вовлечены перестановкой в цикл , а относительно элементов , – что оставляет их на месте, . Для циклической перестановки вводится специальное обозначение

,

и в этом случае называется циклом длины . Например, перестановка

является циклом длины 4. Заметим, что при использовании этого обозначения необходимо указывать степень перестановки, поскольку циклические перестановки разной степени, но с одинаковым набором вовлеченных в цикл элементов, обозначаются одинаково. Например,

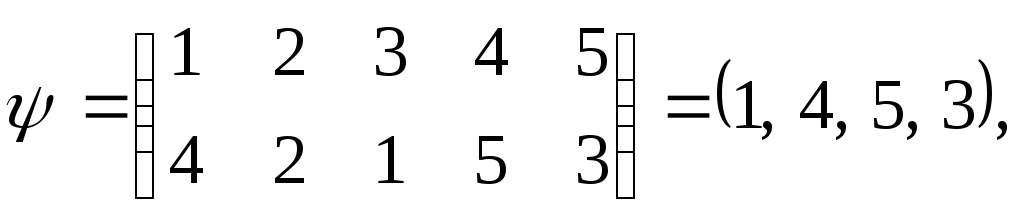
но , т.к. , а .

Два цикла и называются независимыми, если числа, участвующие в их однострочной записи, различны. В противном случае циклы и называются зависимыми. Например, циклы и независимы, а циклы и зависимы.

Предложение 3.1. Любую перестановку , можно представить в виде произведения конечного числа независимых циклов.

◄ Пусть и произвольный элемент такой, что . Обозначив и далее по индукции , цикл строим так,

,

где – первый элемент, совпадающий с одним из предыдущих элементов в записи этого цикла. Отсюда следует, что . В самом деле, если , где , тогда и не удовлетворяет указанному выше условию. После того, как цикл построен, в качестве берем любой элемент, не вошедший в однострочную запись цикла и удовлетворяющий условию , и аналогично циклу строим цикл ,

.

Ввиду того, что есть биективное отображение, циклы и независимы. Продолжая этот процесс, после конечного числа шагов мы получим независимых циклов , обладающих тем свойством, что каждый элемент , удовлетворяющий условию , попадает в запись одного и только одного цикла. Непосредственной проверкой с применением принципа равенства отображений легко убедиться, что . ►

Пример 4. Следующую перестановку

(3.11)

Разложить в произведение независимых циклов.

◄ Применяя алгоритм, описанный при доказательстве предложения 3.1, получаем,

, (3.12)

где все циклы, стоящие в правой части, являются перестановками десятой степени, т.е.

и аналогично для циклов и . ►

Цикл длины 2 называется транспозицией. Транспозиция называется простой, если .

Предложение 3.2. Любую перестановку степени , , можно представить как в виде произведения конечного числа транспозиций, так и в виде произведения конечного числа простых транспозиций.

◄ Для доказательства справедливости первой части утверждения достаточно проверить, что любой цикл можно представить в виде произведения конечного числа транспозиций, а после этого воспользоваться предложением 3.1. В самом деле, пусть цикл длины , . Непосредственной проверкой, применяя принцип равенства отображений, можно убедиться в том, что

. (3.13)

Тогда в силу предложения 3.1 любую перестановку , отличную от , можно представить в виде произведения конечного числа транспозиций. Если же , тогда , где – произвольная транспозиция, так как

.

Теперь покажем, что любую транспозицию можно представить в виде произведения нечетного числа простых транспозиций. Пусть , где . Тогда транспозицию можно записать в виде , где . Непосредственной проверкой убеждаемся в справедливости равенства

, (3.14)

в правой части которого стоит произведение простых транспозиций. Для доказательства справедливости второй части утверждения остается воспользоваться его первой частью. ►

Пример 5. Перестановку вида (3.11) разложить в произведение транспозиций.

◄ Обратимся к разложению (3.12) перестановки в произведение циклов. Так как второй цикл – транспозиция, в произведение транспозиций нужно разложить лишь циклы и . Воспользовавшись формулами (3.13), получаем, что

.

Поэтому искомое разложение перестановки имеет вид

. ►

Пример 6. Следующую перестановку разложить в произведение простых транспозиций.

.

◄ Разлагая в произведение циклов, получаем, что

,

где все циклы являются транспозициями, причем – простая транспозиция. По формуле (3.14)

,

,

Откуда

. ►

Перестановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетной, если она разлагается в произведение нечетного числа транспозиций. На данном этапе введенное определение не является корректным, так как не обсуждена возможность (а точнее невозможность) одновременного разложения произвольной перестановки в произведения как четного, так и нечетного числа транспозиций. На самом деле четность числа транспозиций, на произведение которых разлагается данная перестановка, не зависит от способа её разложения в это произведение. Для того, чтобы доказать этот факт, нужно ввести и изучить еще одно понятие, связанное с перестановками, понятие инверсии.

Пусть , и элементы и где , переводятся перестановкой соответственно в элементы и .

Будем говорить, что пара образует инверсию в перестановке , если , а . В противном случае будем говорить, что пара инверсии не образует.

Пример 7. Пусть . Пары , взятые из нижнего ряда записи перестановки , инверсии образуют, так как , а , а , а . В то же время пары , , , также взятые из нижнего ряда записи , инверсии не образуют, так как и , и , и .

Ясно, что относительно каждой пары можно сказать, образует ли она инверсию или нет. В связи с этим через обозначим число инверсий, имеющихся в перестановке . Очевидное правило подсчета этого числа состоит в следующем. Если задана своей канонической записью, тогда число таково, столько раз в нижней строке большее число стоит левее меньшего.

Пример 8. Для перестановки,

,

так как

,

а в ряду большее число стоит левее меньшего три раза: , , .

Предложение 3.3. Умножение произвольной перестановки , , , справа на простую транспозицию меняет четность числа .

◄ На самом деле, умножение перестановки справа на простую транспозицию , меняет число на 1. Действительно,

.

Если , то пара в инверсии не образовывала, а после умножения на инверсию образует. Если , то эта пара в инверсию образовывала, а после умножения на инверсии не образует. Остальные элементы , после умножения на в записи перестановки остались на месте. Поэтому порождаемое ими количество инверсий не изменилось. Итак, . ►

Следующее предложение позволяет обосновать корректность определения четных и нечетных перестановок.

Предложение 3.4. Для того, чтобы произвольную перестановку -ой степени можно было представить в виде произведения четного (нечетного) числа транспозиций, необходимо и достаточно, чтобы число было четным (нечетным).

◄ Необходимость. Пусть , где – транспозиция. В силу предложения 3.2 каждая транспозиция разлагается в произведение нечетного числа простых транспозиций. Но тогда перестановка представима в виде произведения четного числа простых транспозиций , где – сумма четного числа (числа ) нечетных чисел (чисел простых транспозиций). Транспозиция имеет одну инверсию, . В силу предложения 3.3 умножение на простую транспозицию справа меняет четность числа , т.е. число – четное.

Достаточность. Пусть число – четное. Допустим противное, что перестановка представима в виде произведения нечетного числа транспозиций . Так как транспозиция представима в виде произведения нечетного числа простых транспозиций, , то перестановка тоже представима в виде произведения нечетного числа простых транспозиций , где – сумма нечетного числа нечетных чисел. Рассуждая дальше так же как и при доказательстве необходимости, получаем, что число – нечетное. Полученное противоречие говорит о том, что предположение о представимости в виде произведения нечетного числа транспозиций неверно, т.е. перестановка может быть представлена лишь в виде произведения четного числа транспозиций. ►

Предложение 3.5. Как четные, так и нечетные перестановки составляют половину всех перестановок -ой степени, .

◄ На множестве введем отображение , действующее по правилу , где – фиксированная транспозиция. Отображение обратимо, так как , и следовательно, взаимнооднозначно. Но при этом отображении все четные перестановки переходят в нечетные, а все нечетные – в четные. Поэтому числа всех четных и всех нечетных перестановок -ой степени должны быть одинаковы и равны . ►

Другие свойства перестановок читатель найдет в [3], гл.1, §8.