1.3. Центр ваги .

Центром ваги тіла – називається центр паралельних сил ваги його елементарних частинок .

Центр паралельних сил – це точка , яка лежить на лінії дії рівнодійної даної системи паралельних сил і не змінює свого положення при одночасному повороті всіх сил навколо точок прикладання , в одну і ту ж сторону на один і той самий кут .

Якщо ж тіло можна поділити на визначену кількість частин , у яких положення ваги відоме , то координати центра С ваги будуть :

Де - вага окремої частини ; n – кількість частин ;

- Координати центра ваги окремої частини відносно вибраної системи координат .

Центр ваги об’єму :

Якщо тіло однорідне , то вага частин пропорційна їх об’ємам ,

Тобто де - вага одиниці об’єму .

В цьому випадку координати центра ваги об’єму можна знайти за формулами :

Вирази в чисельниках носять назву статичних моментів об’єму відносно координатних площин yoz , xoz , xoy відповідно .

Центр ваги плоскої фігури .

Якщо тіло являє собою плоску однорідну фігуру , то вага частин пропорційна їх площинам і координати центра ваги фігури можна визначити за формулами :

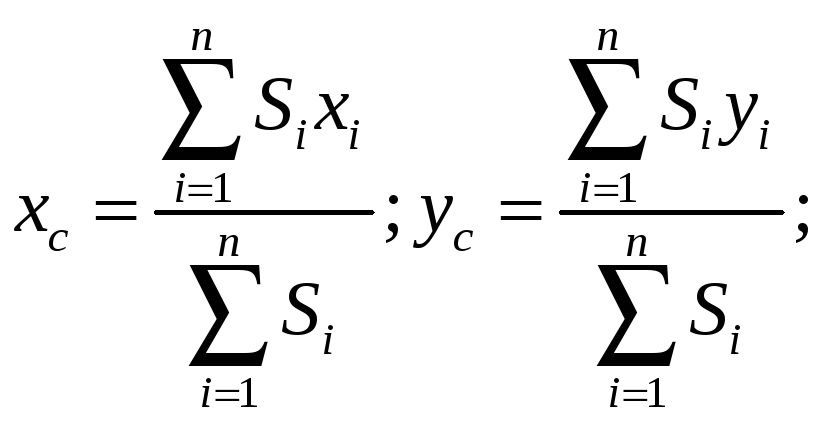
Вирази носять назву статичних моментів площини відносно осей x i y .

Метод від’ємних площин .

Якщо плоска фігура має вирізи , то відповідні їм площі слід вважати від’ємними при застосуванні вище приведених формул .

2.КІНЕМАТИКА

Кінематика – розділ теоретичної механіки , в якому вивчаються рух тіла з геометричної точки зору , тобто без врахування сил , що діють на ці тіла .

2.1.Кінематика точки

Система відліку – система координат зв”язана з тілом , відносно якого визначаються положення інших тіл в різні моменти часу . Задати рух відносно деякої системи відліку - значить задати умови , які дозволяють знайти положення точки або тіла в любий момент часу .

Матеріальна точка – це тіло , яке має вагу , розмірами якого можна знехтувати , при вивчені руху .

Механічний рух – це проста зміна положення одного тіла відносно іншого .

Швидкість – це фізична величина , що характеризує бистроту зміни положення тіла з часом .

Прискорення – це фізична величина , що характеризує бистроту зміни швидкості з часом .

Дотичне прискорення – характеризує бистроту зміни модуля швидкості з часом , направлене по дотичній до траєкторії точки .

Нормальне прискорення – характеризує бистроту зміни напряму швидкості з часом направлене по нормалі до траєкторії до центра кривизни .

Рівняння , що дозволяють визначити положення точки у вибраній системі відліку в будь-який момент часу , називаються кінематичними рівняннями руху точки і виражають закон руху точки .

Три основні способи визначення руху точки :

1.Векторний : - закон руху ;

- швидкість точки ;

- прискорення точки ;

2.Координатний :

- швидкість точки ;

- модуль швидкості ;

- проекції вектора швидкості на осі координат ;

- напрямні косинуси

- прискорення точки ;

- модуль прискорення точки ;

- проекції прискорення на осі координат ;

- напрямні косинуси .

3.Натуральний

При натуральному способі визначення руху повинні бути відомі :

а) траекторія руху точки ;

б) початок відліку і напрямок відліку дугової координати ;

в) закон зміни дугової координати ;

- швидкість точки ;

- величина швидкості точки ;

- прискорення точки ;

- дотичне прискорення ;

-нормальне прискорення ;

де - радіус кривизни траекторії в даній точці.

4.На відміну від декартових координат початок натуральної системи завжди співпадає з точкою М яка рухається , тобто натуральні осі координат знаходяться в спостерігаючому русі .

5. Часткові випадки руху точки :

а) прямолінійний

б) криволінійний

в) рівномірний

г) рівнозмінний

2.2. Кінематика твердого тіла .

2.2.1. Поступальний рух твердого тіла .

2.2.2. Обертання твердого тіла .

2.2.3. Плоско – паралельний рух твердого тіла .

2.2.4. Складний рух точки .

2.2.5. Додавання обертань .

2.2.КІНЕМАТИКА ТВЕРДОГО ТІЛА .

2.2.1. Поступальний рух твердого тіла.

Поступальним називається такий рух тіла , при якому яка завгодно пряма , проведена в тілі , залишається при русі паралельною сама собі

Теорема про траєкторії швидкості і прискорення точок твердого тіла при поступальному русі .

При поступальному русі твердого тіла всі його точки описують конгруентні (однакові ) траєкторії мають геометрично рівні швидкості і прискорення .

Тому поступальний рух твердого тіла можна вивчити , вивчивши рух однієї його точки ( здебільшого це центр мас ) , застосувавши теорію кінематики точки .

2.2.2. Обертання твердого тіла .

Обертанням твердого тіла навколо нерухомої осі називається рух тіла , при якому в тілі ( або нерухомому просторі зв”язаному з тілом ) має місце нерухома пряма . Ця пряма є віссю обертання . Кожна точка тіла описує при його обертанні коло , радіус якого дорівнює відстані від даної точки до осі обертання .

Рівняння обертання має такий вигляд :

Тобто положення тіла визначається кутом повороту його навколо осі обертання ( кут вимірюється в радіанах ) .

Кутова швидкість характеризує бистроту зміни кута повороту тіла навколо осі обертання з часом і дорівнює похідній від кута повороту по часу :

Кутове прискорення характеризує бистроту зміни швидкості з часом і дорівнює першій похідній від кутової швидкості по часу або другій похідній від кута повороту по часу :

При прискореному обертанні кутове прискорення додатнє , при сповільненому – від”ємне . Кут повороту можна виразити загальним числом обертів тіла за весь період обертання :

Кутову швидкість задають в техніці числом обертів за хвилину . При цьому перевод кутової швидкості n об/хв в радіани за секунду проводиться за формулою :

Кут повороту , кутова швидкість і кутове прискорення характеризують рух твердого тіла в цілому .

Формули за допомогою яких визначаються кінематичні величини будь-якої точки тіла :

• шлях точки по колу : ;

• лінійна швидкість точки : ;

• дотичне прискорення точки : ;

• нормальне прискорення точки : ;

• повне прискорення точки : ;

• кут між напрямом повного і нормального прискорень : .

Передавання обертального руху тіла :

Передавання обертального руху :

В зубчастих колесах числа зубців z пропорційні радіусам коліс r тому можна писати

2.2.3. Плоскопаралельний рух твердого тіла .

Плоскопаралельним називають такий рух твердого тіла , при якому всі точки тіла рхаються в площинах , паралельних деякій нерухомій площині .

Вивчення плоскопаралельного руху можна звести до руху плоскої фігури в її площині , або відрізка прямої цієї фігури . Положення фігури в даний момент часу визначається координатами довільної її точки О, яку називають полюсом і кутом повороту фігури навколо полюса .

Рівняння руху фігури мають такий вигляд :

Перші два рівняння характеризують поступальний рух фігури , а третє – обертальний .

Кутова швидкість і кутове прискорення не залежать від вибору полюса .

Теорема про швидкості точок плоскої фігури :

Лінійна швидкість будь-якої точки М фігури при її плоскому русі дорівнює геометричній сумі швидкості полюса О і обертальної швидкості даної точки навколо полюса :

Теорема про проекції швидкостей двох точок плоскої фігури :

В плоскому русі фігури проекції швидкостей кінців А і В відрізка будь-якої прямої АВ на фігурі на напрям цієї прямої рівні між собою :

пр.на AB = пр.на AB ;

або

де і - кути між і і напрямом прямої АВ відповідно .

За теоремою Ейлера – Шаля , плоский рух у даний момент часу можна розглядати як обертальний рух навколо центра обертання , або миттєвого центра швидкостей.

Миттєвий центр швидкостей (МЦШ) –це точка незмінно зв”язана з плоскою фігурою , швидкість якої в кожний даний момент часу дорівнює нулю .

Окремі випадки визначення миттєвого центра швидкостей :

Теорема про прискорення точок плоскої фігури :

Прискорення будь-якої точки М плоскої фігури при її плоскому русі дорівнює геометричній сумі прискорень полюса А і прискорення точки М в її обертальному русі навколо полюса :

За полюс фігури приймається точка А прискорення якої відоме

М – будь-яка точка плоскої фігури : і - дотичне і нормальне прискорення точки М при обертанні навколо полюса А .

і направлене в бік .

направлена від М до полюса А .

- кутові швидкість і прискорення фігури в даний момент часу .

Миттєвий центр прискорень .

Миттєвий центр прискорень – це точка незмінно зв’язана з плоскою фігурою , прискорення якої в кожний даний момент часу = 0.

Q – Миттєвий центр прискорень (МЦП).

Деякі випадки знаходження МЦП.

1. Відомі , з точки А провести промінь під кутом в бік . На промені відкласти відрізок AQ :

2. Відомі : напрямки прискорень точок А і В , З точок А і В провести промені під кутомвідкладаючи кути за напрямком