2.5. Построение интерполяционных сплайновых кривых при помощи сплайн - функций

Ранее мы всегда оговаривали, что в интерполяционной таблице все узлы сетки различны и упорядочены по возрастанию . Как строить интерполяционные сплайны, если узлы сетки совпадают между собой или не упорядочены по возрастанию? В таких случаях решением задачи интерполяции являются кривые, заданные параметрически Приведем алгоритм для описания параметрических уравнений кривой, описанный в книге /9/.

Пусть задана интерполяционная таблица , , причем узлы сетки не упорядочены и могут совпадать между собой. Требуется построить кривую, последовательно проходящую через все точки интерполяционной таблицы.

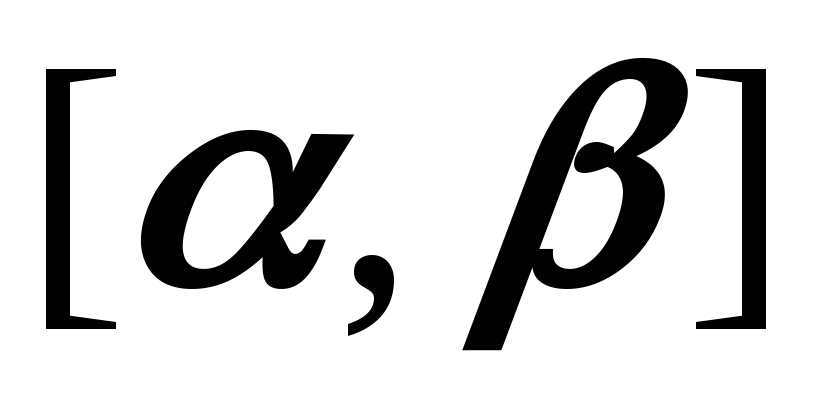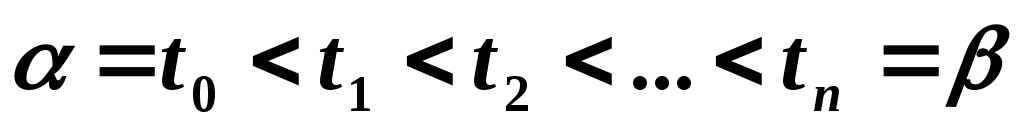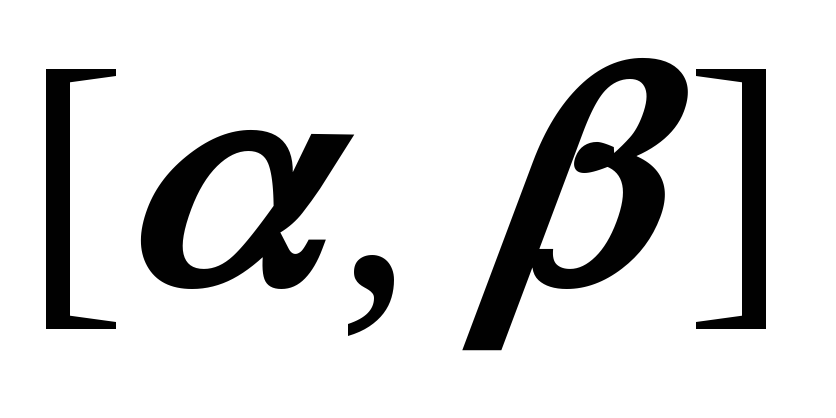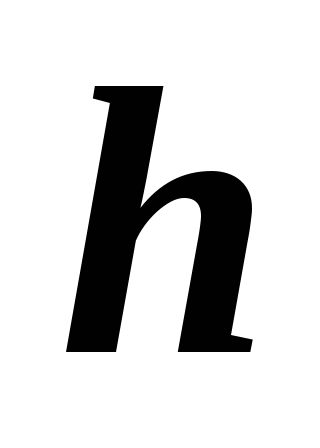1. На произвольном отрезке изменения параметра вводится вспомогательная сетка, узлы которой упорядочены и различны: . Число узлов сетки совпадает с числом заданных точек . В качестве отрезка можно выбрать отрезок [0,1], а шаг по переменной выбрать равномерный, т.е. .

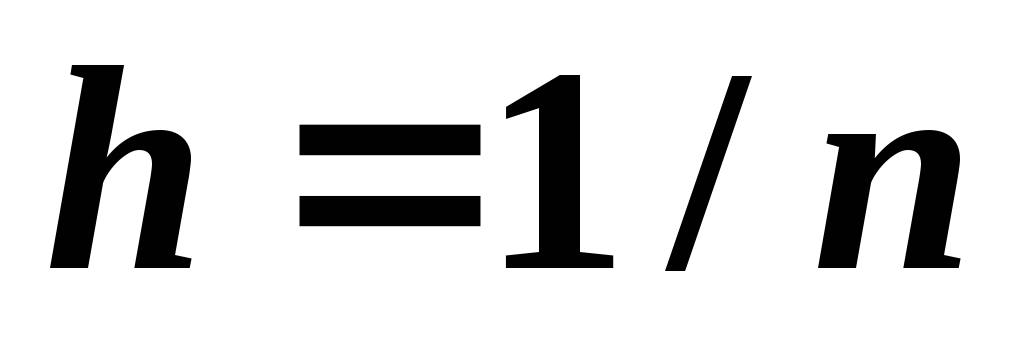2. По известной интерполяционной таблице , 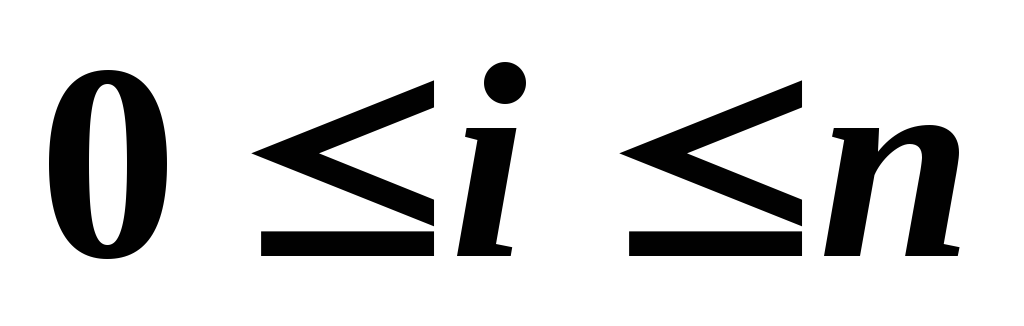и вспомогательной сетке строятся две вспомогательные интерполяционные таблицы:

, , .

Отметим, что в построенных вспомогательных интерполяционных таблицах узлы сетки упорядочены и различны, и по этим таблицам единственным образом могут быть построены интерполяционные сплайны и .

3. По каждой из вспомогательных интерполяционных таблиц строятся соответствующие интерполяционные сплайн – функци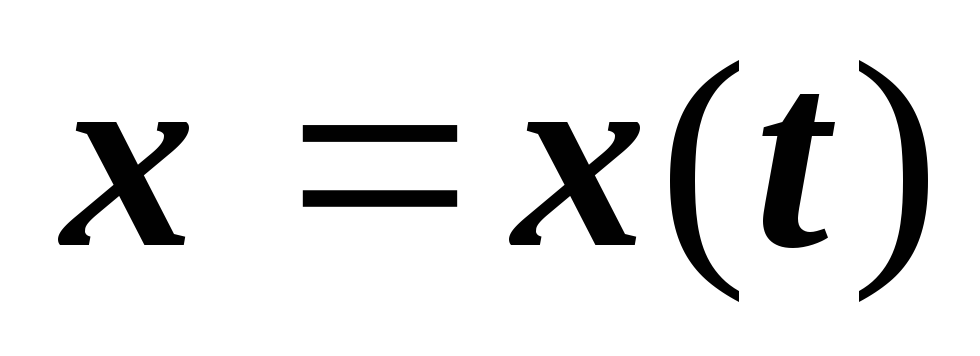и и .

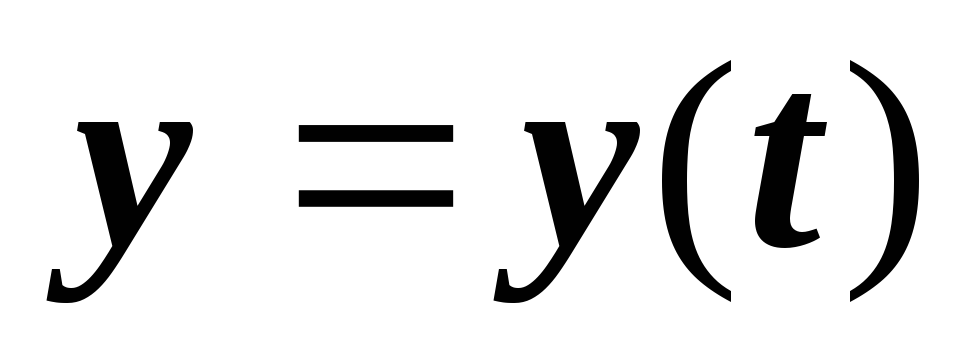Таким образом, получается кривая, последовательно проходящая через все точки заданной интерполяционной таблицы (рис. 2.3).

2.6. Примеры решения задач

Задача 1. По данной интерполяционной таблице построить интерполяционный линейный сплайн.

Решение. Пусть задана интерполяционная таблица:

	0	1	2
	3	2	5

Таким образом, задано , , и , , , .

Линейный сплайн в данном случае () определяется формулой

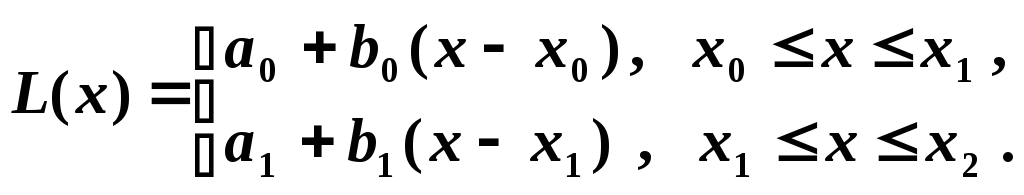
Для нахождения коэффициентов и воспользуемся формулами и , . Получаем , , , . Запишем

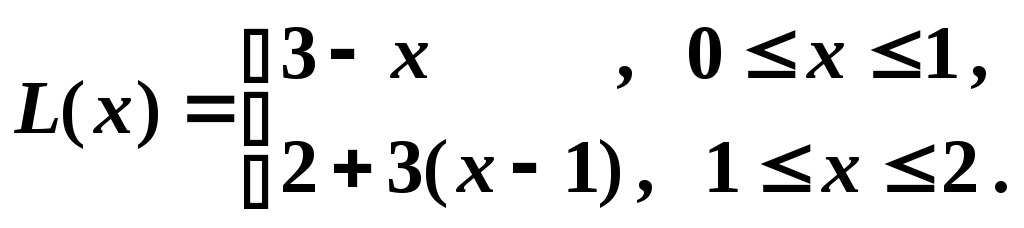
Проверим, что - интерполяционный сплайн, для этого вычислим значения при Получаем , , , следовательно, - интерполяционный сплайн.

Ответ:

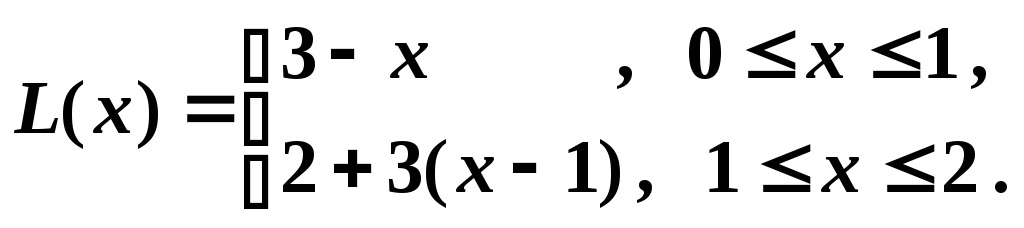
Задача 2. Построить систему линейных уравнений для нахождения коэффициентов интерполяционного параболического сплайна по заданной интерполяционной таблице и краевому условию.

Решение. Пусть задана интерполяционная таблица

	0	1	2
	3	2	7

и краевое условие: , т.е. , , ; , , , .

Решение задачи заключается в построении системы линейных уравнений относительно коэффициентов параболического сплайна . Так как , то параболический сплайн записывается следующим образом:

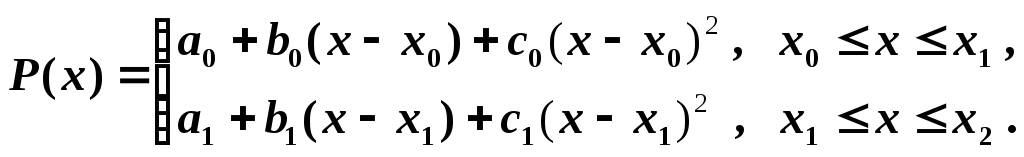
Неизвестных коэффициентов , и шесть, требуется записать шесть линейных уравнений. Первые три уравнения вытекают из условий: , . Получаем: , , , где , . В нашем случае равномерный шаг равен 1. Получаем три уравнения: , , .

Одно уравнение вытекает из краевого условия . Запишем формулу для производной сплайна:

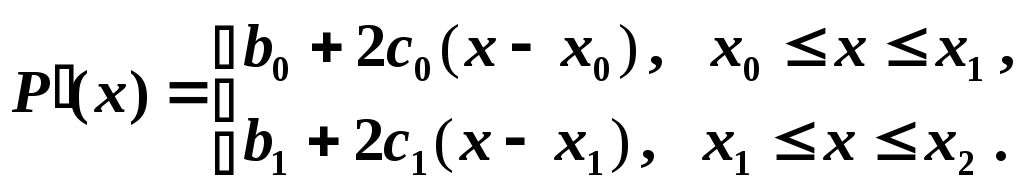
Из краевого условия получаем уравнение или . Еще два уравнения получаем из условия, что параболический сплайн является непрерывно дифференцируемой функцией во всех внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел . Запишем формулу сплайна в виде:

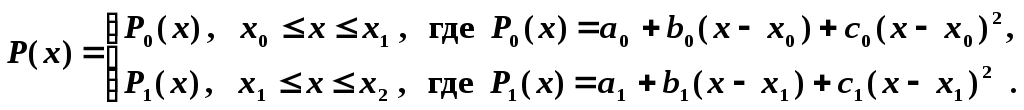
Из непрерывности сплайна вытекает уравнение или , а из непрерывности производной сплайна вытекает, что или .

Ответ: Запишем систему линейных уравнений:

Отметим, что мы рассмотрели случай правого краевого условия (). Случай левого краевого условия рассматривается аналогично. Например, если вместо условия задано условие , то в системе линейных уравнений четвертое уравнение нужно заменить на следующее: .

Задача 3. Построить систему линейных уравнений для нахождения коэффициентов интерполяционного кубического сплайна по заданным краевым условиям и интерполяционной таблице.

Решение. Пусть задана интерполяционная таблица

	0	1	2
	2	5	6

и краевые условия: и , т.е. , , , , , , , . Требуется построить систему линейных уравнений относительно коэффициентов кубического сплайна . Так как , то кубический сплайн записывается следующим образом:

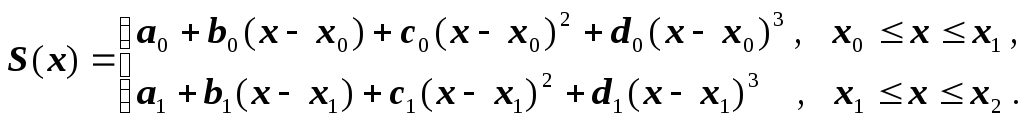
Неизвестных коэффициентов восемь, требуется записать восемь линейных уравнений. Первые три уравнения вытекают из условий , . Получаем: , , . Запишем первые три уравнения: , , . Два уравнения вытекают из краевых условий. Запишем формулу для производной сплайна:

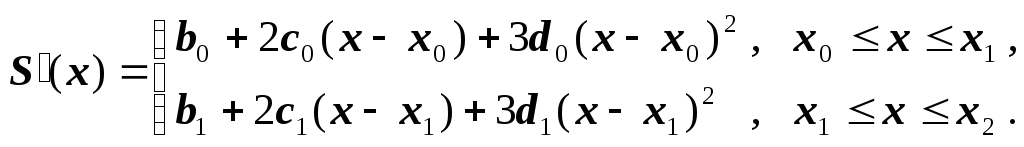
Из левого краевого условия вытекает уравнение . Из правого условия вытекает уравнение . Еще три уравнения получаем из условия, что кубический сплайн является дважды непрерывно дифференцируемой функцией во всех точках отрезка , в том числе и во внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел . Запишем формулу сплайна в виде:

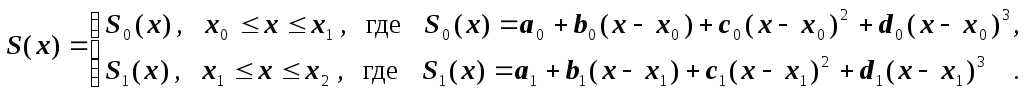
Из непрерывности сплайна вытекает уравнение . А из непрерывности первой и второй производной сплайна следуют уравнения и . Получаем:

, , .

Ответ: Запишем систему линейных уравнений:

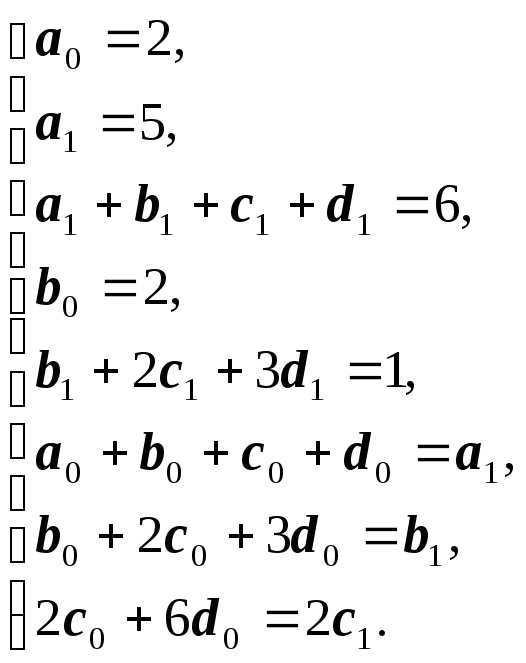
Задача 4. Определить, является ли функция линейным сплайном, где

Решение. Запишем функцию в виде:

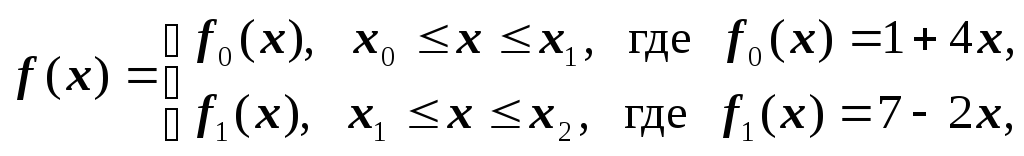
. Для того чтобы функция являлась линейным сплайном, одновременно должны выполняться два условия:

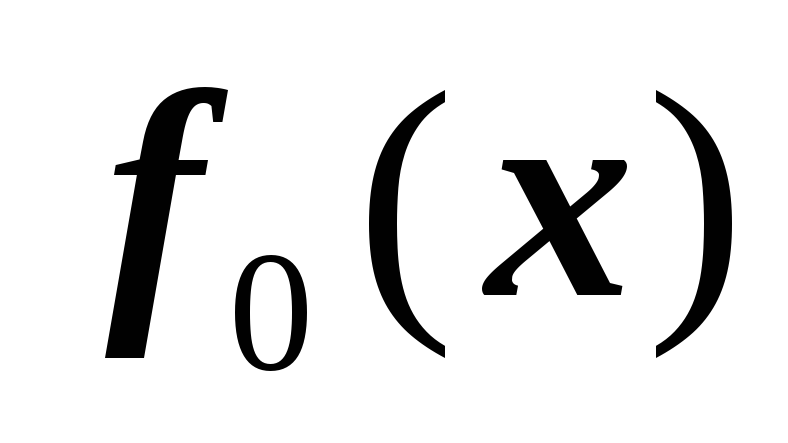1. функции и 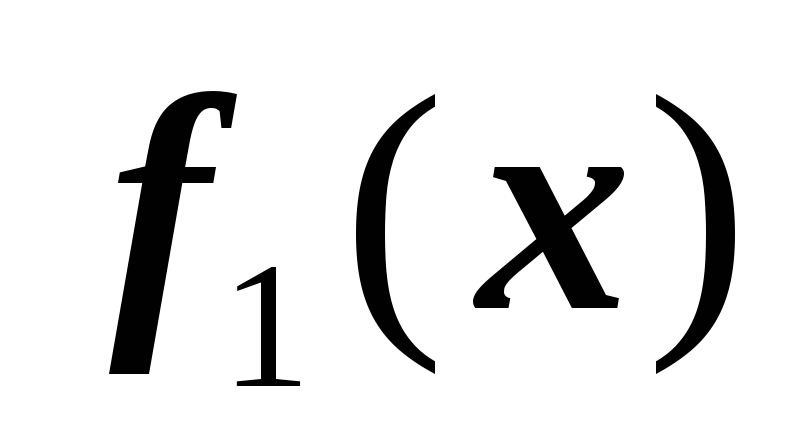- полиномы первой степени;

2. функция 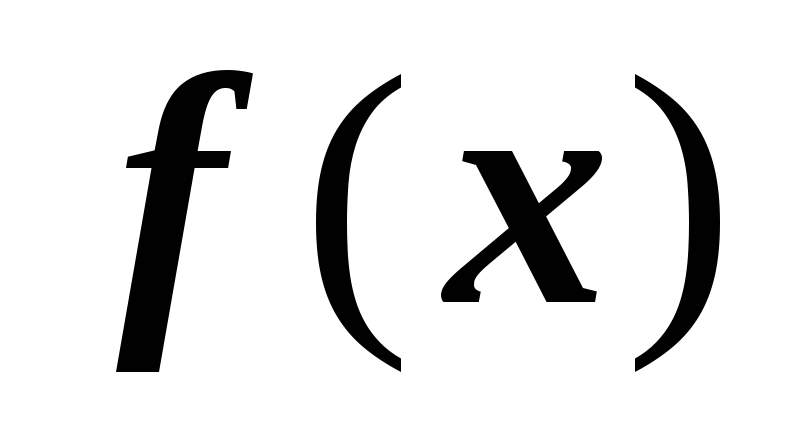- непрерывная функция на отрезке .

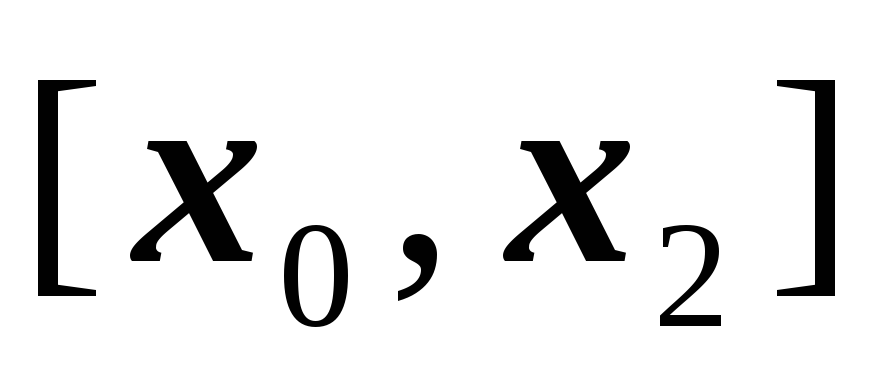Если хотя бы одно из этих условий не выполнено, то функция не является линейным сплайном, если же они выполняются одновременно, то является линейным сплайном. Проверим эти условия. Первое условие выполнено, так как функции и являются полиномами первой степени. Второе условие, при выполнении первого условия, достаточно проверить во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел . Поэтому второе условие при выполнении первого условия достаточно проверить только в точке , т.е. нужно проверить выполнение равенства . Вычислим и . Так как , то - непрерывная функция на отрезке . Оба условия выполнены, следовательно, функция является линейным сплайном.

Ответ: функция является линейным сплайном.

Задача 5. Определить, является ли функция параболическим сплайном, удовлетворяющим краевому условию , где ,

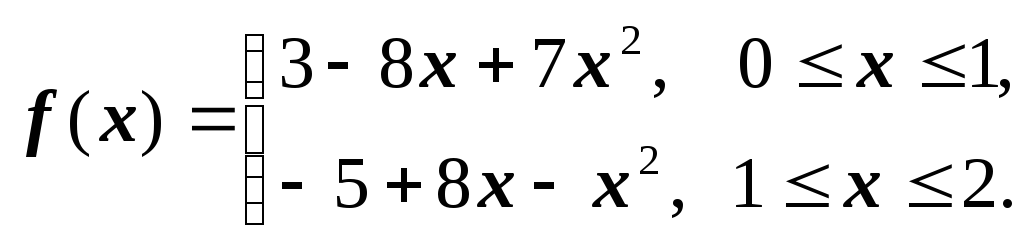
Решение. Запишем функцию в виде:

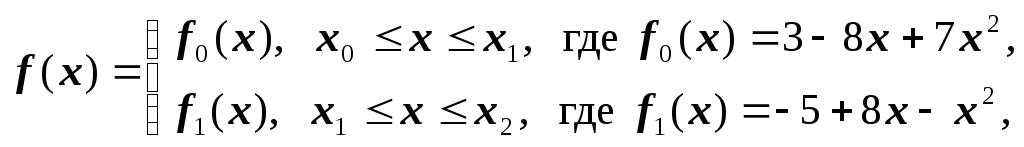
, , . Для того чтобы функция являлась параболическим сплайном, удовлетворяющим краевому условию , одновременно должны выполняться три условия:

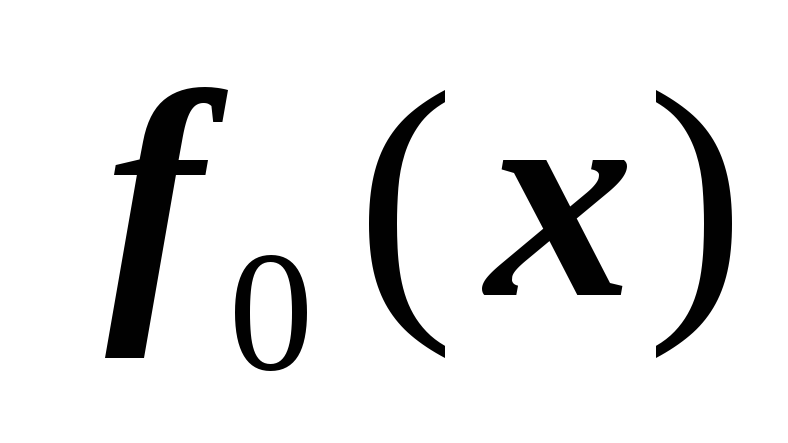1. функции и 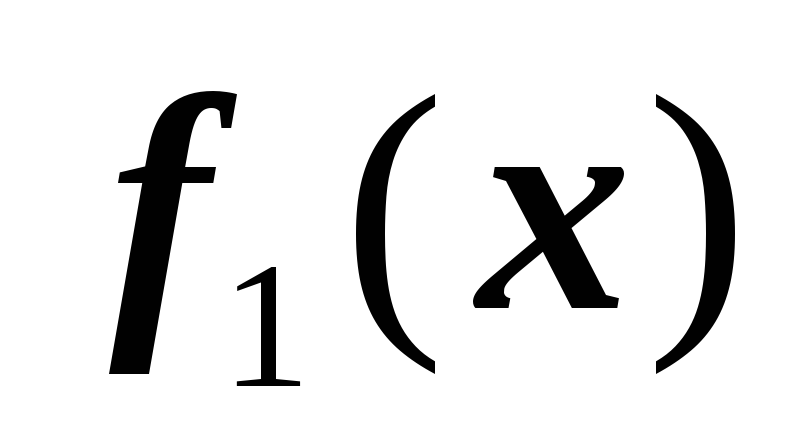- полиномы второй степени;

2. функция - непрерывно дифференцируемая функция на отрезке ;

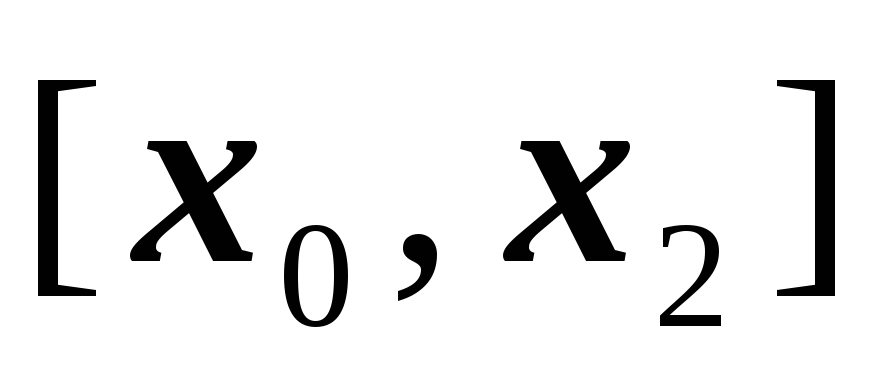3. функция 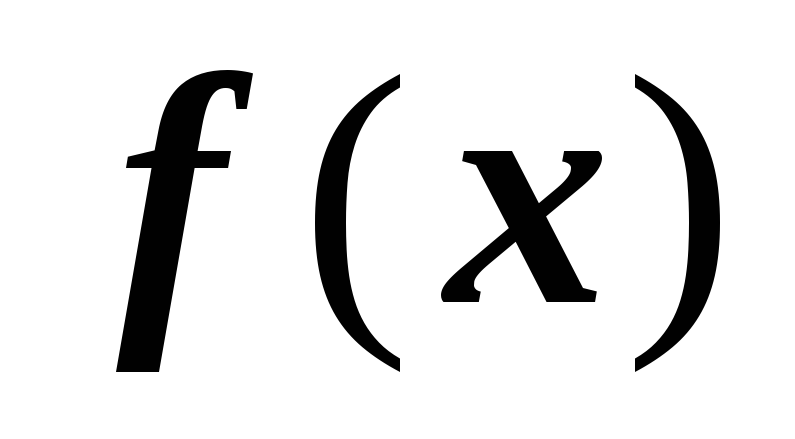удовлетворяет краевому условию .

Если хотя бы одно из этих условий не выполнено, то функция не является параболическим сплайном, удовлетворяющим заданному краевому условию. Проверим эти условия. Первое условие выполнено, так как функции и являются полиномами второй степени. Второе условие, при выполнении первого условия, достаточно проверить только во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел . Поэтому второе условие, при выполнении первого условия, достаточно проверить только в точке , т.е. нужно проверить выполнение равенств и . Вычислим , ; , , , . Так как , то - непрерывно дифференцируемая функция на отрезке . Для проверки третьего условия вычислим значение производной функции в точке : . Так как , то третье условие выполнено.

Три условия выполняются одновременно, следовательно, функция является параболическим сплайном, удовлетворяющим краевому условию .

Ответ: функция является параболическим сплайном, удовлетворяющим краевому условию .

Задача 6. Определить является ли функция естественным кубическим сплайном, где:

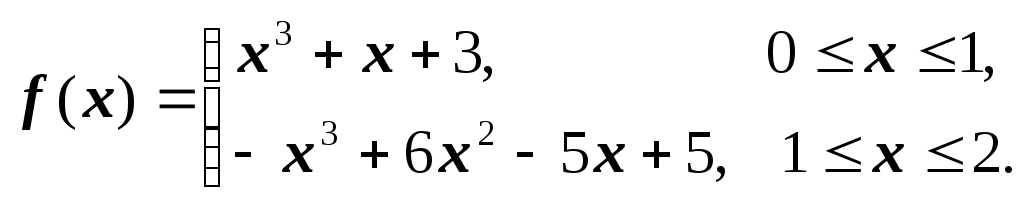
Решение. Запишем функцию в виде:

, , . Для того чтобы функция являлась естественным кубическим сплайном, одновременно должны выполняться три условия:

1. функци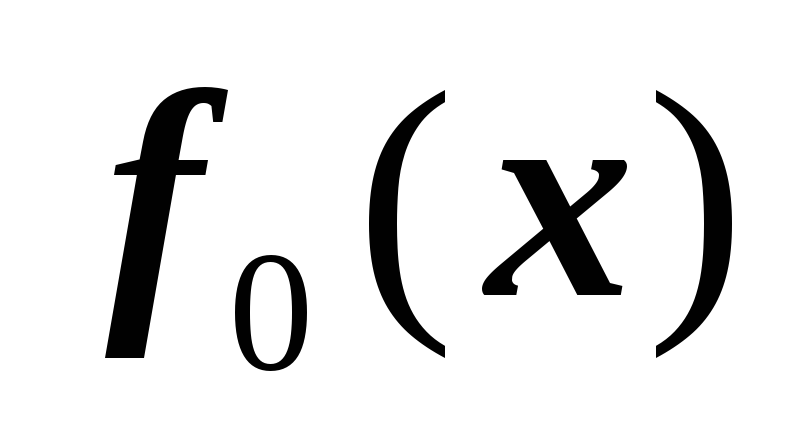и и - полиномы третьей степени;

2. функция 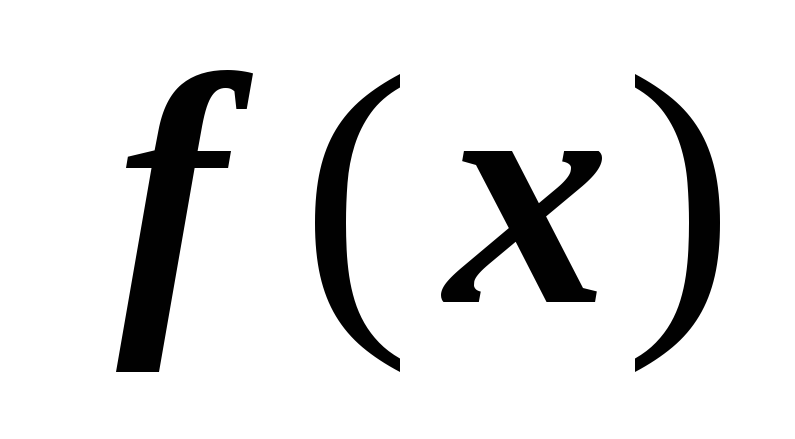- дважды непрерывно дифференцируемая функция на отрезке ;

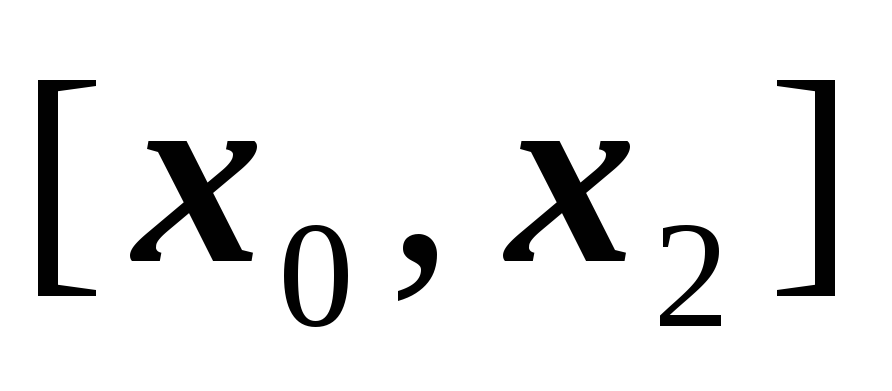3. функция 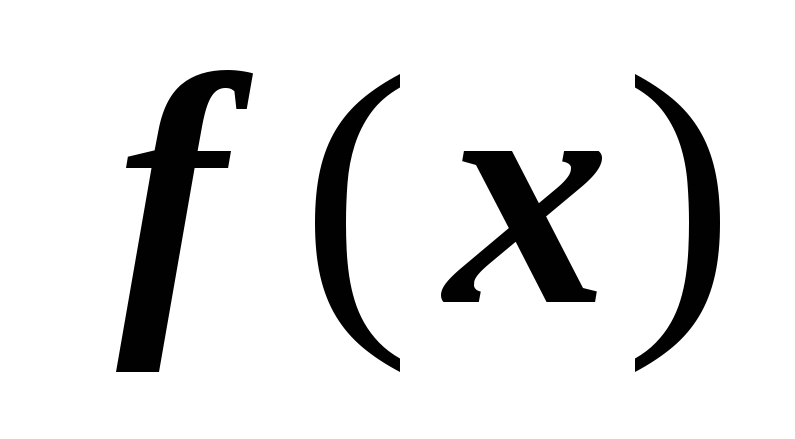удовлетворяет двум краевым условиям: , .

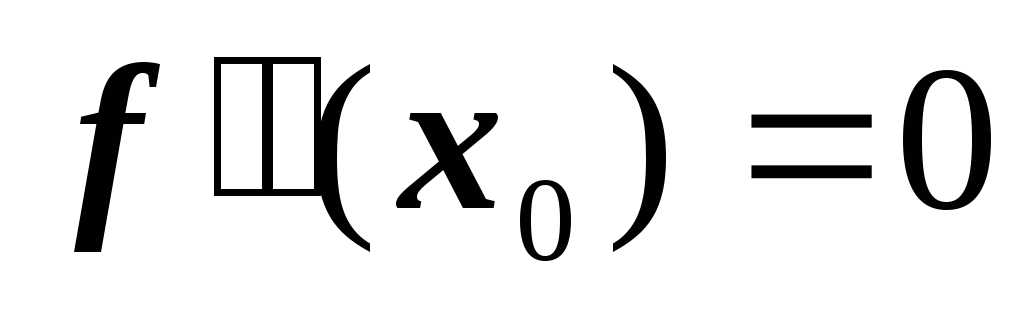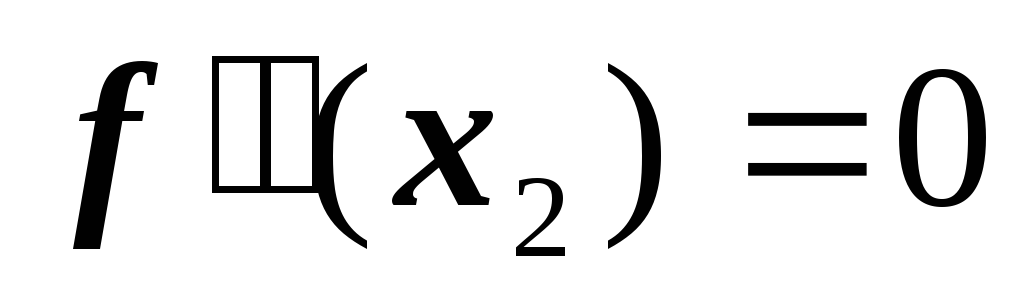Если хотя бы одно из этих условий не выполнено, то функция не является естественным кубическим сплайном. Проверим эти условия. Первое условие выполнено, так как функции и являются полиномами третьей степени. Второе условие, при выполнении первого условия, достаточно проверить только во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел . Поэтому второе условие, при выполнении первого условия, достаточно проверить только в точке , т.е. нужно проверить выполнение равенств: , и . Вычислим , ; , , , ; , , , . Так как , то - дважды непрерывно дифференцируемая функция на отрезке . Для проверки третьего условия вычислим значения второй производной функции в краевых точках: и . Третье условие выполнено.

Три условия выполняются одновременно, следовательно, функция является естественным кубическим сплайном.

Ответ: функция является естественным кубическим сплайном.