Нахождение коэффициентов естественного интерполяционного кубического сплайна

Из определения естественного интерполяционного кубического сплайна мы получаем систему линейных уравнений с невырожденной матрицей, число уравнений равно . Если мы будем решать эту систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента, то нам потребуется арифметических действий и памяти. Но известен устойчивый алгоритм нахождения коэффициентов сплайна, для реализации которого требуется арифметических действий и памяти. Опишем этот алгоритм.

1. По явным формулам находятся коэффициенты , .

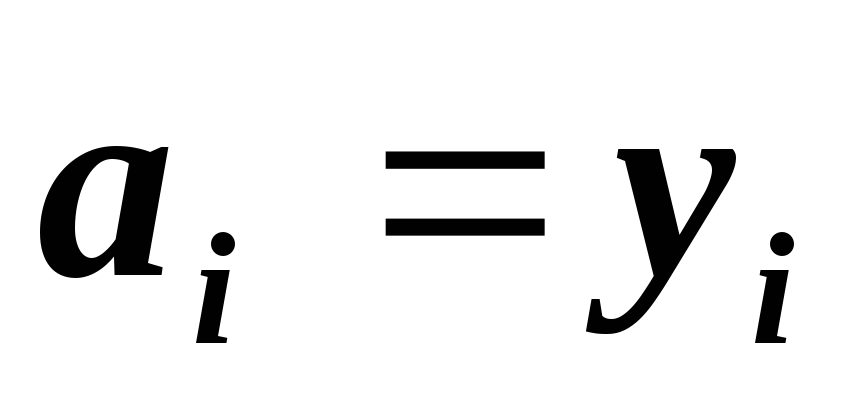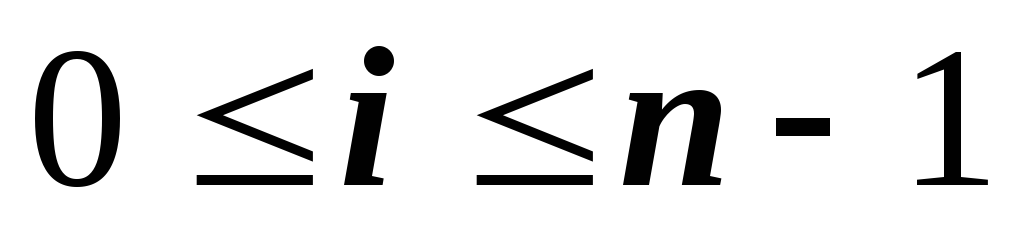2. Коэффициенты 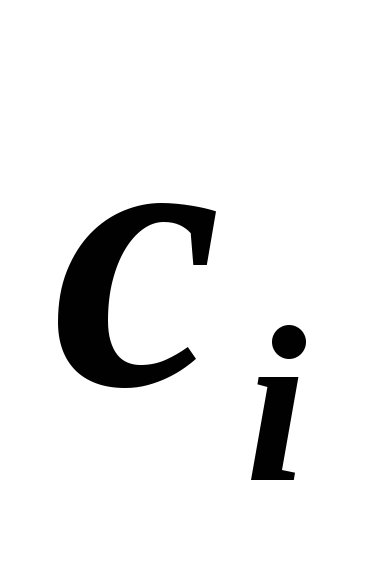находятся из решения системы линейных уравнений размерности 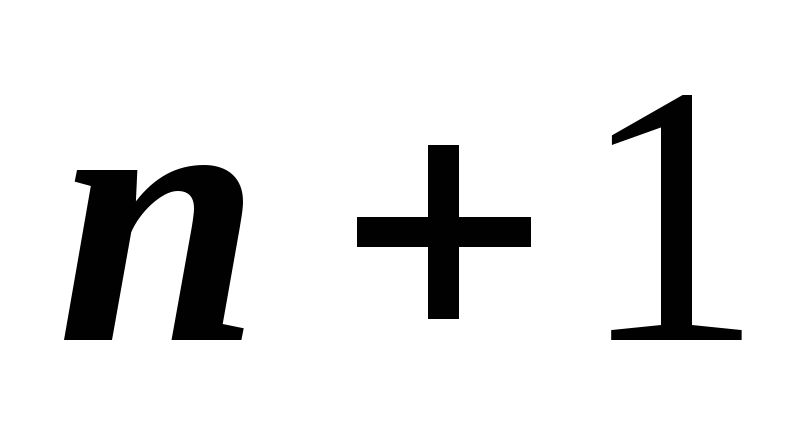с невырожденной трехдиагональной матрицей методом прогонки. Запишем эту систему линейных уравнений для случая равномерного шага

Условие на применение метода прогонки для решения этой системы уравнений следующее: . Это условие выполнено, если все узлы сетки различны.

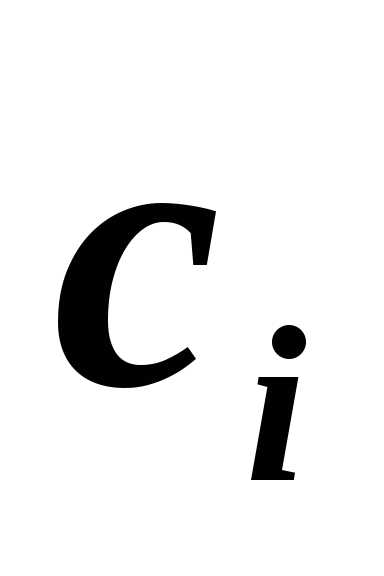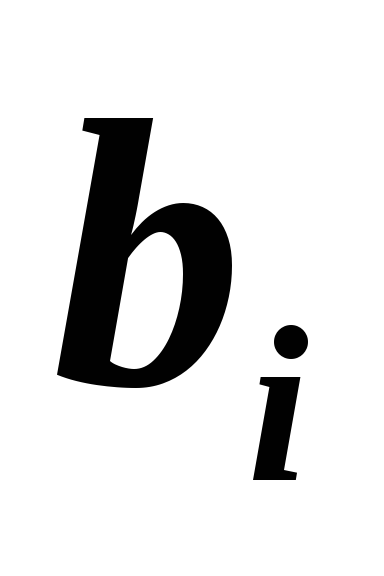3. Зная и , находим коэффициенты и по явным формулам:

, , .

Отметим, что для удобства записи системы линейных уравнений, определен дополнительный коэффициент , равный нулю. Уравнения и вытекают из равенства нулю второй производной естественного интерполяционного кубического сплайна на концах отрезка .

Теорема (о сходимости). Пусть функция - непрерывная функция на отрезке , тогда интерполяционный кубический сплайн сходится к при , стремящемся к нулю, для любой точки из отрезка , то есть , где , .

Теорема (оценка погрешности). Пусть . Тогда для любой точки справедливы следующие оценки погрешности:

, , ,

где , а положительные константы , , и не зависят от .

Таким образом, при уменьшении равномерного шага в два раза, погрешность интерполяции кубическим сплайном уменьшается в 16 раз.

Производная интерполяционного кубического сплайна – это непрерывно дифференцируемая кусочно-параболическая функция, то есть параболический сплайн:

, , .

Отметим, что производная интерполяционного кубического сплайна не является интерполяционным сплайном для производной функции.

Нахождение значений естественного интерполяционного кубического сплайна и его производных

Как и для параболического сплайна, сначала находим номер отрезка, содержащего точку , по формуле . Зная все коэффициенты , , , и номер отрезка , находим значение естественного интерполяционного кубического сплайна в точке, принадлежащей отрезку ,

.

Для вычисления значений сплайна и его производных в точке , введем дополнительные коэффициенты: , , . Ранее уже был определен коэффициент .

Значения первой и второй производных естественного интерполяционного кубического сплайна вычисляются по формулам

, .

Сложность вычислительного алгоритма построения интерполяционного кубического сплайна та же, что и у параболического и линейного сплайнов. Число арифметических действий, необходимых для построения интерполяционного кубического сплайна, пропорционально числу отрезков (), объем памяти также пропорционален числу отрезков ().

Так как интерполяционный кубический сплайн хорошо приближает гладкие функции (теорема о сходимости, оценка погрешности) и имеет минимальную сложность, то на практике для гладких функций при решении задач интерполяции и численного дифференцирования используется именно интерполяционный кубический сплайн.

2.4. B-сплайны

B-сплайны (базовые, фундаментальные, базисные сплайны) – это функции, определенные на отрезке и образующие некоторый базис, который позволяет представить любой сплайн в виде линейной комбинации соответствующих B-сплайнов. Так же, как произвольный вектор , принадлежащий плоскости , можно единственным образом представить в виде линейной комбинации базисных векторов и , а именно , так и произвольный сплайн можно единственным образом представить в виде линейной комбинации соответствующих базисных сплайнов.

B-сплайном нулевой степени, построенным на отрезке по сетке , называется функция вида:

B-сплайн степени может быть отличен от нуля только на отрезках , примыкающих друг к другу. Например, кубический B-сплайн отличен от нуля на отрезке , а линейный B – сплайн отличен от нуля на отрезке (рис. 2.2).

Любой линейный сплайн на отрезке можно представить в виде линейной комбинации B-сплайнов первой степени:

.

Любой кубический сплайн на отрезке также может быть единственным образом представлен в виде линейной комбинации кубических B-сплайнов. Такой подход позволяет уменьшить объем памяти, необходимый для построения сплайна.