Результат работы программы

Значение функции f в точке x=0.15 равно 0.14943

Значение сплайна P в точке x=0.15 равно 0.14945

Значение производной функции f'в точке x=0.15 равно 0.9887

Значение производной функции P'в точке x=0.15 равно 0.9883

2.3. Интерполяционный кубический сплайн

Наиболее часто на практике используется интерполяционный кубический сплайн. Кубический сплайн - это дважды непрерывно дифференцируемая функция, состоящая из «кусочков» полиномов третьей степени. Обозначим кубический сплайн. Для каждого из отрезка

,

где , , и - числовые коэффициенты. Таким образом, на каждом отрезке , четыре неизвестных коэффициента: , , и , а на всем отрезке число неизвестных коэффициентов равно . Следовательно, нам требуется уравнений.

Так как является интерполяционной функцией, то уравнения получаем из условий , . Во всех внутренних узлах сетки (число внутренних узлов равно ) функция должна быть непрерывной, непрерывно дифференцируемой и дважды непрерывно дифференцируемой функцией. Таким образом, три условия в каждой внутренней точке, в итоге условий. В сумме получаем линейных уравнений. Два недостающих условия – это краевые (граничные) условия. Для кубических сплайнов рассматриваются четыре типа краевых условий, в дальнейшем мы будем рассматривать краевое условие вида

.

Определение. Кубический сплайн, удовлетворяющий краевым условиям , называется естественным кубическим сплайном.

Сформулируем определение естественного интерполяционного кубического сплайна.

Определение естественного интерполяционного кубического сплайна. Пусть на отрезке задана сетка , в узлах которой заданы значения ,. Естественным интерполяционным кубическим сплайном называется функция , удовлетворяющая следующим условиям:

1. функция 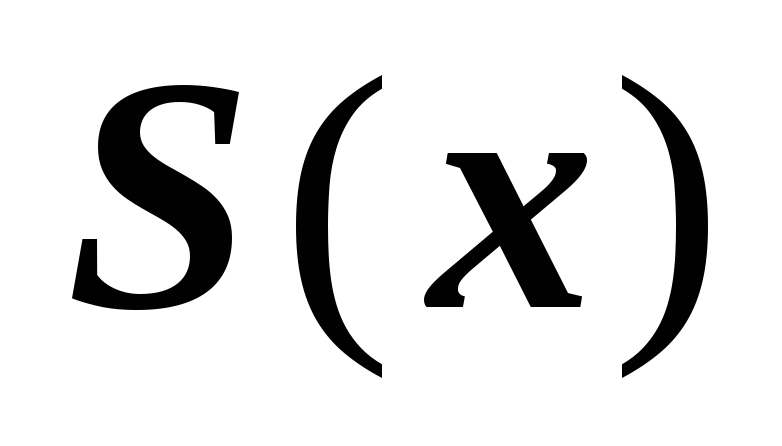– дважды непрерывно дифференцируемая функция на ;

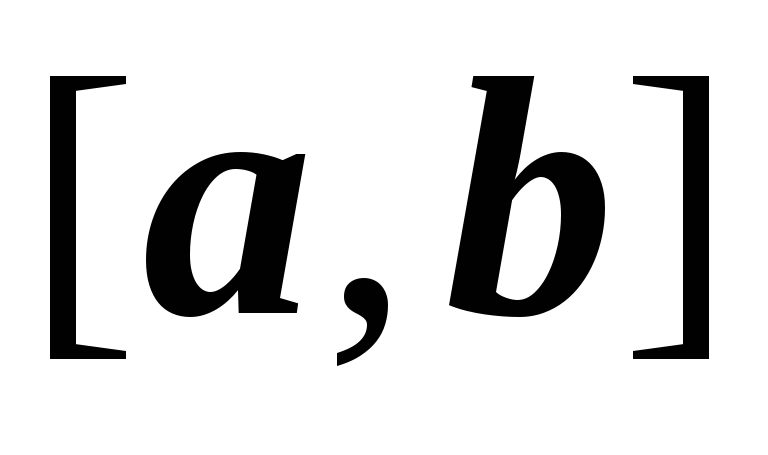
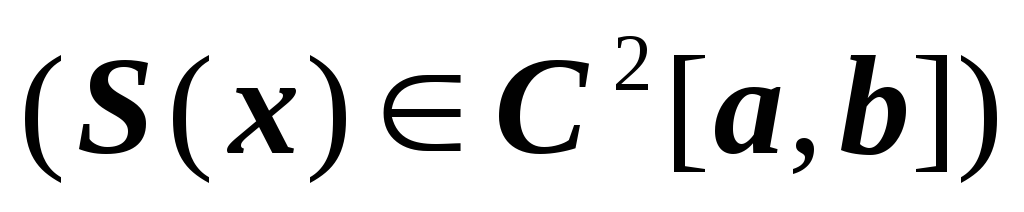2. на каждом из отрезков 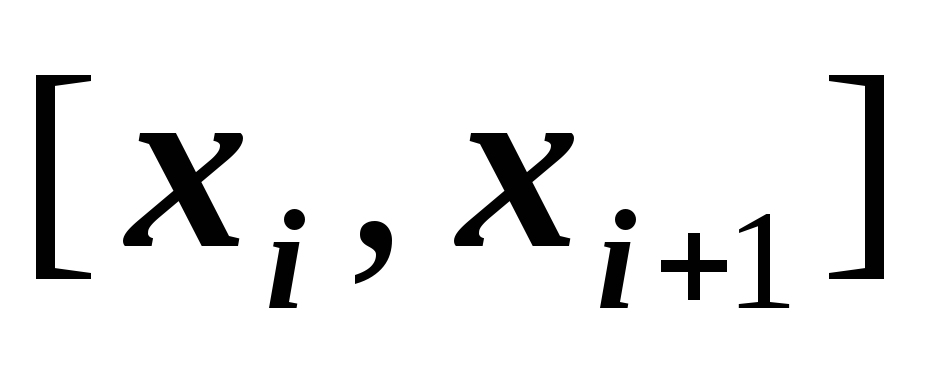функция 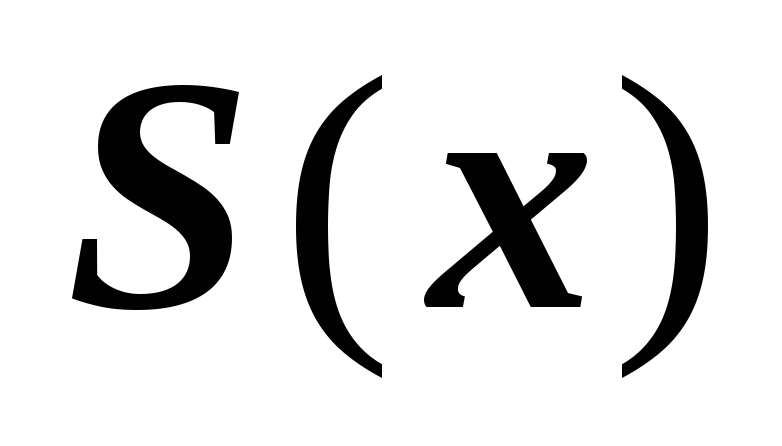является полиномом третьей степени вида

, ;

3. функция 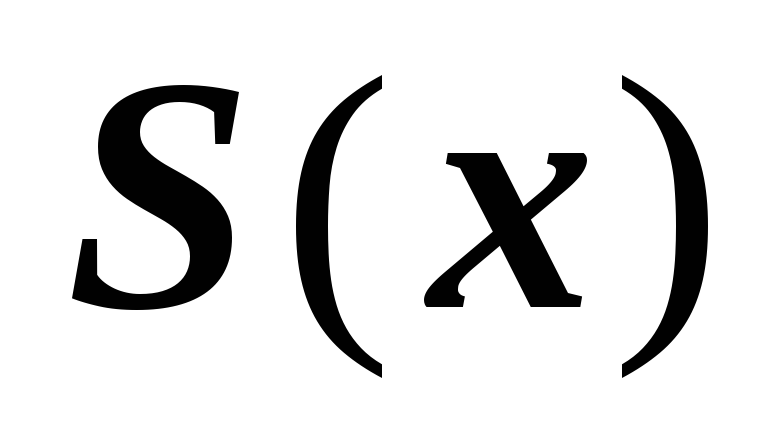– интерполяционная функция, то есть:, ;

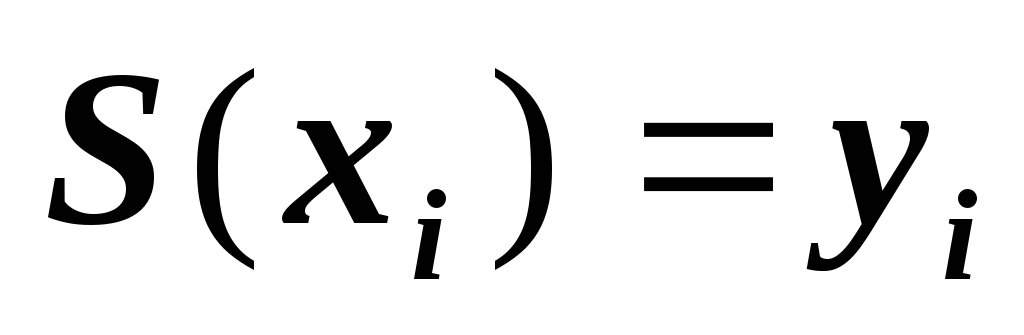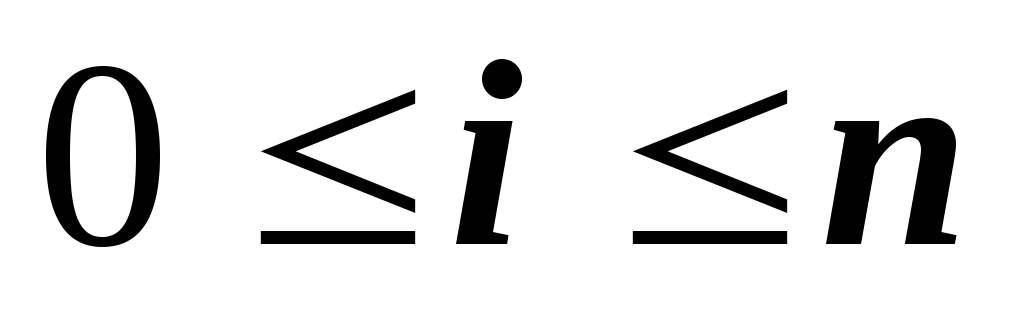4. краевым условиям .

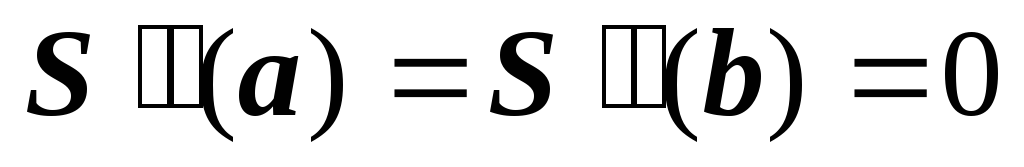Отметим, что, отбросив условие три, мы получаем определение естественного кубического сплайна.

Пример. Функция

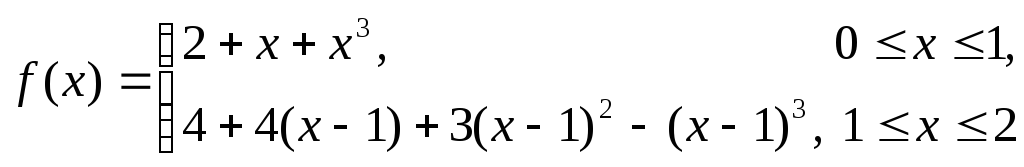
является естественным кубическим сплайном, определенным на отрезке . Эта же функция является естественным интерполяционным кубическим сплайном, удовлетворяющим следующей интерполяционной таблице:

	0	1	2
	2	4	10

Пример программы, которая по интерполяционной таблице строит естественный интерполяционный кубический сплайн, приводится в примере выполнения задания 2 расчетно-графического задания 1.

Теорема существования и единственности. Пусть на отрезке задана интерполяционная таблица , , причем все узлы сетки различны ( при ). Тогда существует единственный естественный кубический сплайн такой, что .

Другими словами, если задана интерполяционная таблица, в которой все узлы сетки различны, то существует единственный естественный интерполяционный кубический сплайн, удовлетворяющий этой таблице.