2.1. Интерполяционный линейный сплайн

Линейный сплайн на отрезке - это непрерывная кусочно-линейная функция. На отрезке введем сетку . Обозначим линейный сплайн. Для каждого из отрезка линейный сплайн определяется следующим образом: , где и - числовые коэффициенты.

Пример . На рис. 2.1 приведен график линейного сплайна. Формула этого сплайна записывается следующим образом:

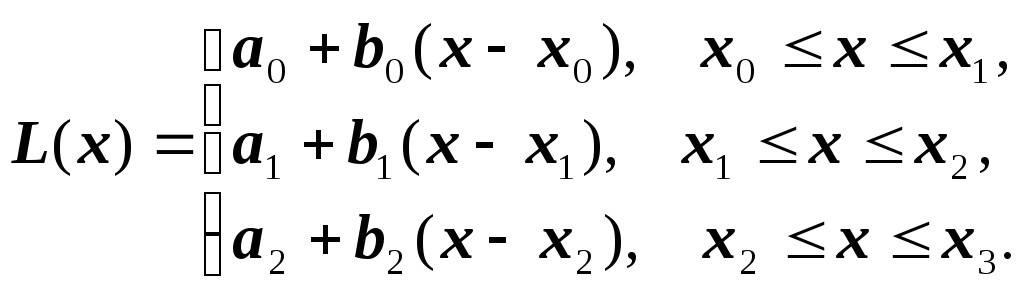
В дальнейшем мы будем рассматривать, как правило, равномерные сетки . Так как сетка состоит из точки, то отрезок разбит на отрезков . На каждом из отрезков линейный сплайн определяется формулой , то есть однозначно определяется двумя коэффициентами: , . На всем отрезке линейный сплайн определяется коэффициентами и , . Для того чтобы однозначно определить интерполяционный линейный сплайн на отрезке , нам требуется уравнений относительно и .

Так как является интерполяционной функцией, то первые уравнения получаем из условия , .

Узлы сетки и называют граничными узлами, а узлы - внутренними узлами сетки. Во всех внутренних узлах сетки (а их число равно ) функция должна быть непрерывна, следовательно, получаем еще уравнение. В сумме получаем линейных уравнений относительно неизвестных и .

Дадим строгое определение интерполяционного линейного сплайна.

Определение интерполяционного линейного сплайна. Пусть на отрезке задана сетка , в узлах которой заданы значения ,. Интерполяционным линейным сплайном называется функция , удовлетворяющая следующим условиям:

1. функция – непрерывная функция на ;

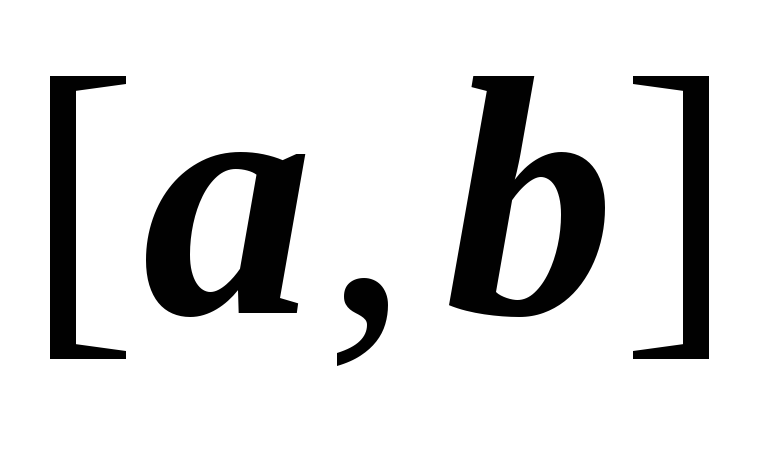
2. на каждом из отрезков 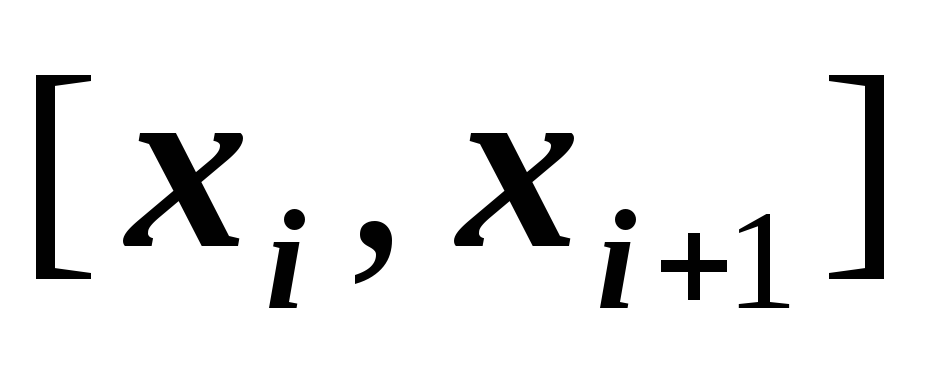функция является полиномом первой степени вида

, ;

3. функция 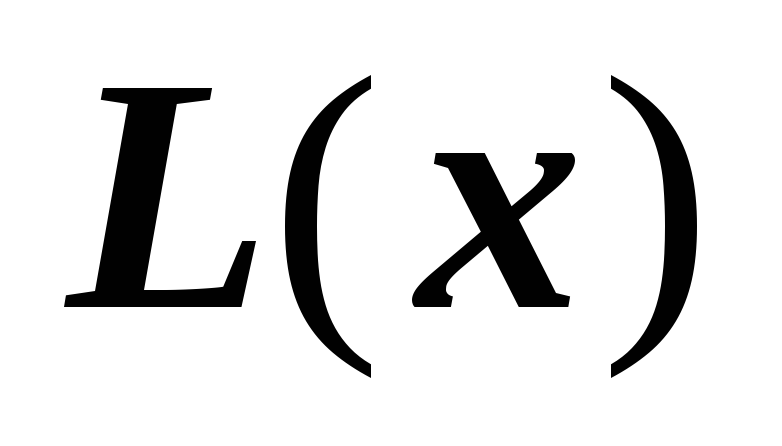– интерполяционная функция, то есть: , .

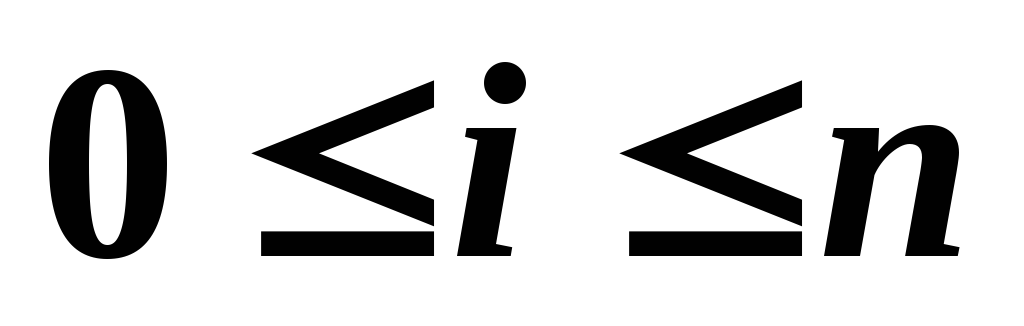Отметим, что из этого определения, отбросив условие три, мы получаем определение линейного сплайна.

Пример. Функция

является линейным сплайном, определенным на отрезке . Эта же функция является интерполяционным линейным сплайном, удовлетворяющим следующей интерполяционной таблице:

	0	1	2
	5	3	7

Пример программы, которая по интерполяционной таблице строит интерполяционный линейный сплайн, приводится в примере выполнения задания 1 расчетно-графического задания 1.

Теорема существования и единственности. Пусть на отрезке задана интерполяционная таблица , , причем все узлы сетки различны ( при ). Тогда существует единственный линейный сплайн такой, что .

Другими словами, для интерполяционной таблицы, в которой все узлы сетки различны, существует единственный интерполяционный линейный сплайн, удовлетворяющий этой таблице.

Отметим, что как и при интерполяции полиномами, требование, чтобы все узлы сетки были различны, является очень важным при интерполяции сплайнами.

Нахождение коэффициентов интерполяционного линейного сплайна

Мы уже отмечали, что из определения интерполяционного линейного сплайна следует система линейных уравнений размерности относительно неизвестных и , . Эта система линейных уравнений имеет единственное решение, если все узлы сетки различны (). Система линейных уравнений легко решается, и мы можем записать формулы для нахождения коэффициентов и :

, , .

Производная линейного сплайна – это кусочно-постоянная функция на отрезке : для из отрезка .