1.2. Метод прогонки для пятидиагональных матриц

Рассмотрим метод прогонки для пятидиагональных матриц с диагональным преобладанием. Запишем систему линейных уравнений:

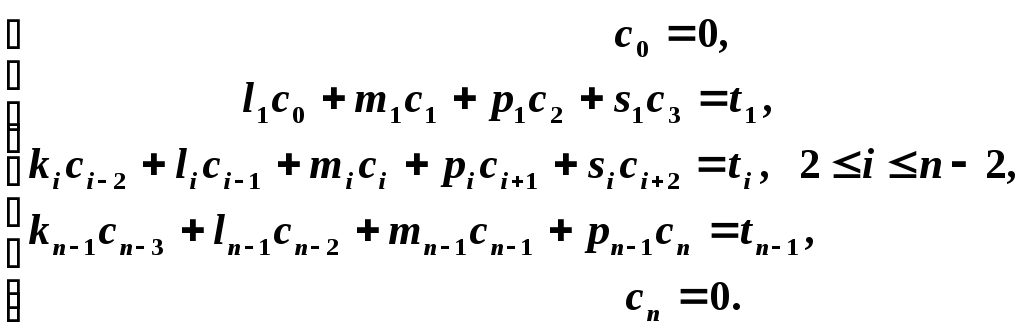
Именно в таком виде записывается система линейных уравнений при нахождении коэффициентов естественного сглаживающего кубического сплайна.

Будем полагать, что выполняются условия диагонального преобладания:

Напомним, что при выполнении этих условий система линейных уравнений имеет единственное решение.

Идея метода прогонки для пятидиагональных матриц заключается в том, что неизвестное представляется в виде: , , где , и - неизвестные числовые коэффициенты, называемые прогоночными коэффициентами.

Приведем формулы метода прогонки.

1. На первом этапе находим значения

, , , .

2. Затем, в порядке возрастания индексов, находим остальные прогоночные коэффициенты по формулам

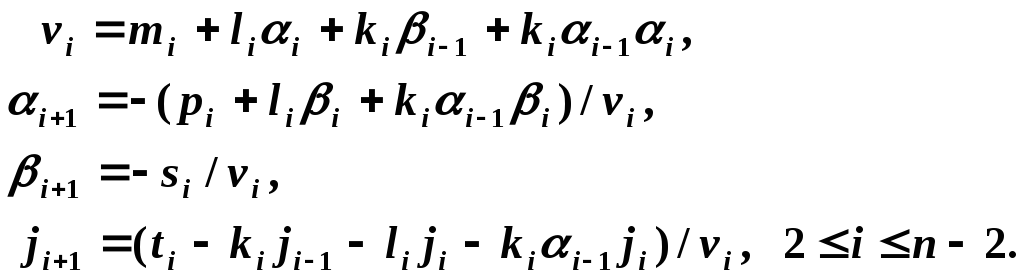
Первые два этапа называют прямой прогонкой.

3. Находим неизвестные 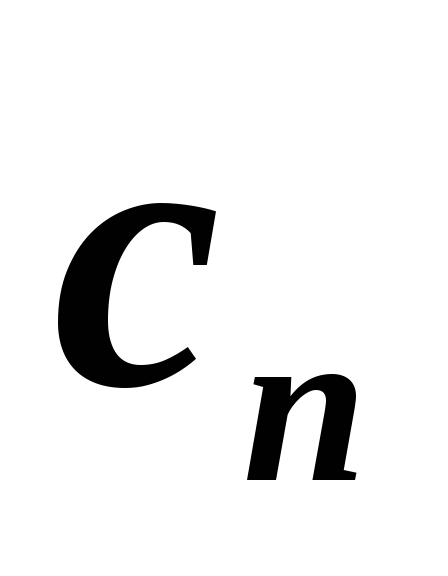и :

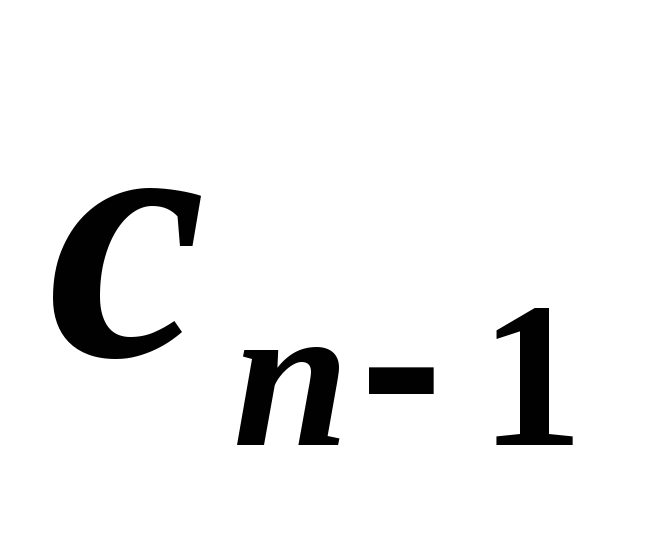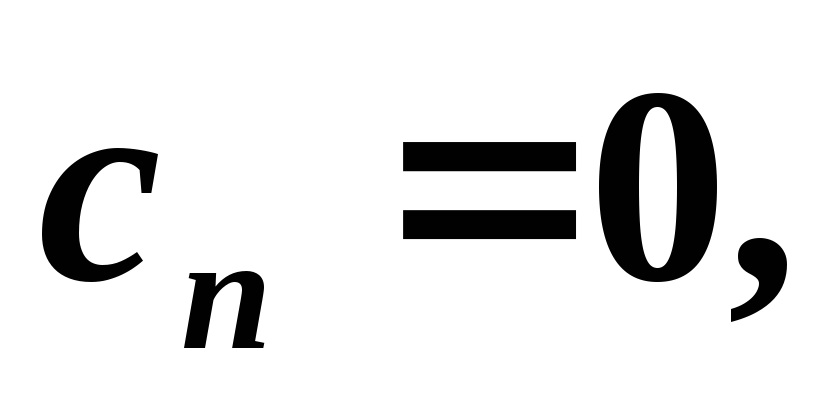
4. Находим неизвестные в порядке убывания индексов:

,

Два последних этапа называют обратной прогонкой.

2. Сплайн – интерполяция

Напомним основные определения.

Определение сетки. Рассмотрим отрезок и конечное множество, состоящее из точек , удовлетворяющих следующему условию:

.

Множество точек называется сеткой на отрезке .

Сетка – это одно из основных понятий. Точки , , называются узлами сетки. Отметим, что в дальнейшем мы будем рассматривать только такие сетки, в которых все узлы сетки различны ( для ) и упорядочены по возрастанию.

Определение интерполяционной таблицы. Пусть заданы вещественные числа . Таблица, состоящая из значений , , называется интерполяционной таблицей, где - узлы сетки, – значения некоторой функции в узлах сетки.

Постановка задачи интерполяции. Пусть на отрезке задана сетка , в узлах которой заданы значения: , , (где - некоторая функция). Требуется построить функцию такую, что

1) , ;

2) достаточно близка к на отрезке .

Другими словами, задача интерполяции заключается в нахождении значений таблично заданной функции в тех точках внутри заданного отрезка, которые не являются узлами сетки.

Постановка задачи численного дифференцирования. Пусть на отрезке задана сетка , в узлах которой заданы значения: , (где - некоторая функция). Требуется найти функцию на отрезке , которая достаточно близка к .

В курсе «Вычислительная математика» мы рассматривали интерполяцию полиномами, в дальнейшем мы будем изучать сплайн-интерполяцию. При решении задачи интерполяции будем полагать, что - интерполяционный сплайн. При решении задачи численного дифференцирования будем полагать, что - производная некоторого сплайна. При этих предположениях о функциях и задачи интерполяции и численного дифференцирования имеют единственное решение.

Сначала мы дадим нестрогое определение сплайна, а затем подробно рассмотрим интерполяционный линейный сплайн, интерполяционный параболический сплайн и интерполяционный кубический сплайн.

Сплайн на отрезке - это функция (как правило, непрерывная), которая является кусочно-полиномиальной, то есть состоит из «кусочков» полиномов одинаковой степени.

Рекомендуемая литература: /7 – 9/.