3.2. Построение естественного сглаживающего кубического сплайна

Для построения естественного сглаживающего кубического сплайна

необходимо уметь вычислять коэффициенты сплайна и Опишем алгоритм нахождения коэффициентов сплайна, для реализации которого требуется арифметических действий и памяти.

1. Коэффициенты находятся из решения системы линейных уравнений размерности с невырожденной пятидиагональной матрицей методом прогонки (п.п.1.2). Запишем эту систему линейных уравнений для случая равномерного шага и одинаковых значений весовых коэффициентов

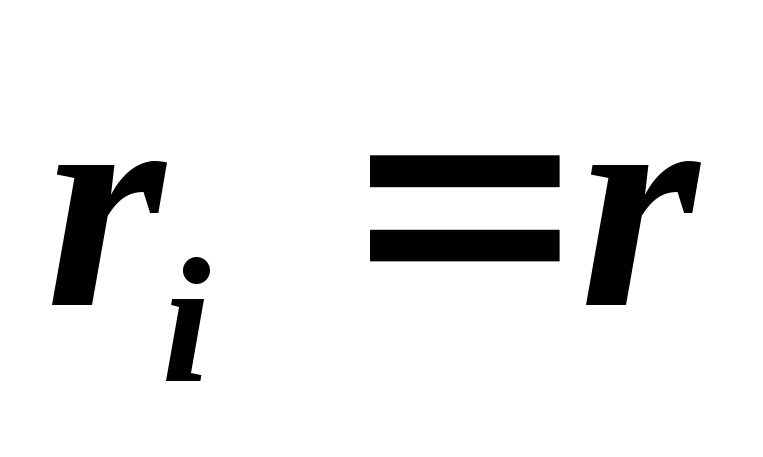
где

Отметим, что при мы получаем систему линейных уравнений с трехдиагональной матрицей (случай естественного интерполяционного кубического сплайна).

2. После нахождения коэффициентов находим где - это значения естественного сглаживающего кубического сплайна в узлах сетки, Значения находится по следующим формулам:

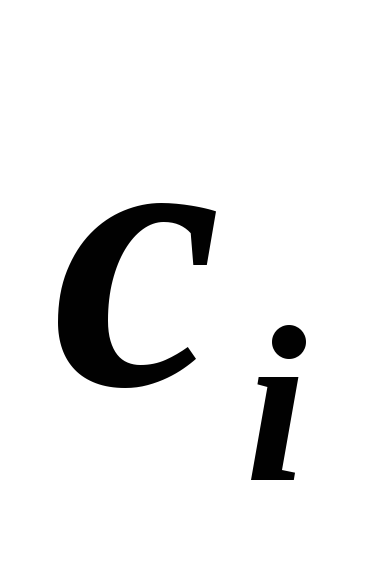3. Зная и 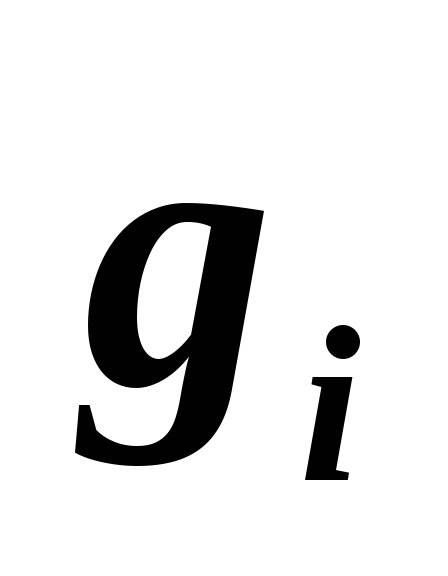, находим коэффициенты , и 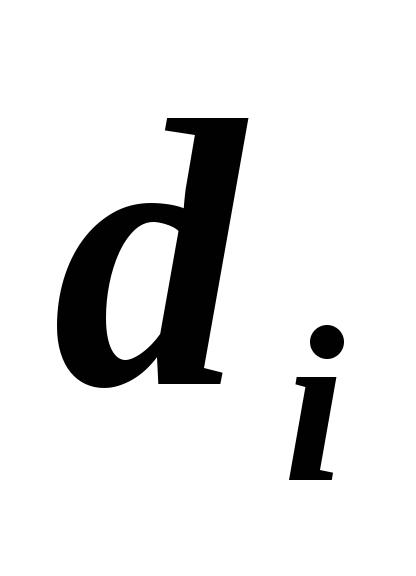по явным формулам

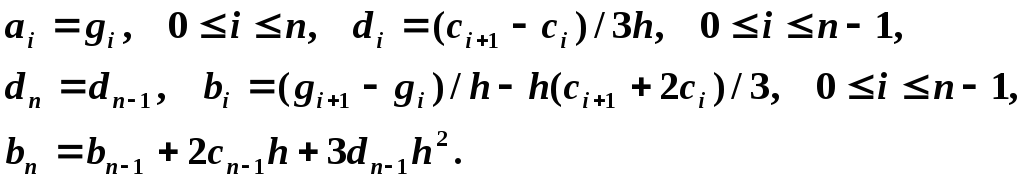
Отметим, что мы сразу привели формулы для дополнительных коэффициентов и , которые потребуются для вычисления значения сплайна и его производных при

Нахождение значений естественного сглаживающего кубического сплайна и его производных

Как и в случае интерполяционных сплайнов, сначала находим номер отрезка, содержащего точку , по формуле . Зная все коэффициенты , , , и номер отрезка , находим значение естественного сглаживающего кубического сплайна в точке, принадлежащей отрезку ,

.

Для вычисления значений сплайна и его производных в точке , используем ранее вычисленные дополнительные коэффициенты , , и .

Значения первой и второй производных естественного сглаживающего кубического сплайна вычисляются по формулам

, .

Сложность вычислительного алгоритма построения сглаживающего кубического сплайна та же, что и у интерполяционного кубического сплайна. Число арифметических действий, необходимых для построения сглаживающего кубического сплайна, пропорционально числу отрезков (), объем памяти также пропорционален числу отрезков ().

4. Аппроксимация

Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции, которая достаточно близко (или наиболее близко) проходит около заданных точек или около заданной функции /1/. Задача аппроксимации существенно отличается от задачи интерполяции (глава 2). Как правило, исходные данные содержат погрешность, и даже в случае незашумленных данных ищется сравнительно простая аналитическая зависимость между заданными x = (x₀, x₁,…, x_n) и y = (y₀, y₁,…, y_n).

Рекомендуемая литература: /1-3, 5-6, 9/.