§ 3.5. Розрахунок потенціалу електричного поля деяких заряджених тіл

Знайдемо потенціали електричних полів деяких заряджених тіл.

а). Потенціал поля рівномірно зарядженої кулі.

Розглянемо кулю радіусом , рівномірно заряджену по об’єму з об’ємною густиною і загальним зарядом ( рис.3.13 ).

З

Рис. 3.13

найдемо різницю потенціалів між двома точками простору 1 і 2 на відстані і від центру кулі в середині кулі . Використаємо формулу різниці потенціалів (3.73)

. (3.86)

Підставимо вираз (3.37) напруженості електричного поля всередині зарядженої кулі у формулу (3.86)

(3.87)

З

Рис.3.14

найдемо різницю потенціалів між двома точками простору 1 і 2 на відстані і від центру кулі ззовні кулі і , як зображено на рис. 3.14.

Підставимо вираз (3.41) напруженості електричного поля ззовні від зарядженої кулі у формулу (3.86)

. (3.88)

Формула (3.88) справедлива також і для точкового електричного заряду .

б). Потенціал поля нескінченної рівномірно зарядженої прямої

Розглянемо нескінченно довгу пряму рівномірно заряджену електричним зарядом з лінійною густиною заряду . Знайдемо різницю потенціалів між двома точками простору 1 і 2 на відстані і від прямої

( рис. 3.15 ). Підставимо вираз (3.48) напруженості електричного поля зарядженої прямої у формулу (3.86)

Рис.3.15

. (3.89)

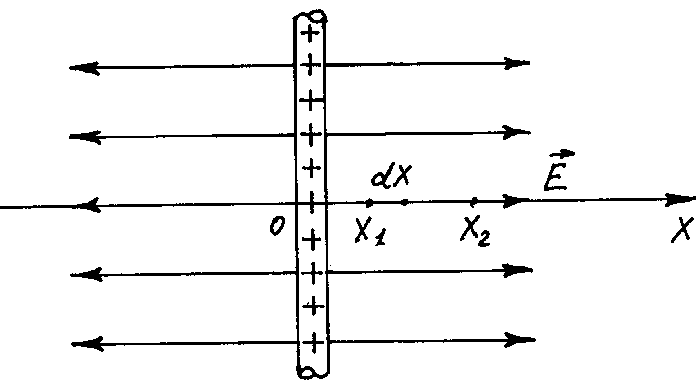
в). Потенціал поля нескінченої рівномірно зарядженої площини

Розглянемо нескінчену площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду . Знайдемо різницю потенціалів між двома точками простору 1 і 2 на відстані і від площини, як зображено на рис. 3.16. Підставимо вираз (3.55) напруженості електричного поля нескінченої рівномірно зарядженої площини у формулу (3.86)

Рис.3.16

. (3.90)

г). Потенціал поля електричного диполя.

Електричним диполем називається система двох однакових за модулем різнойменних зарядів. Плечем диполя називається вектор напрямлений від негативного заряду до позитивного. Дипольним моментом називається векторна фізична величина, рівна добутку позитивного заряду на плече диполя

. (3.91)

Знайдемо потенціал електричного поля в точці А як суму потенціалів двох точкових зарядів, які визначимо за формулою (3.69)

. (3.92)

Р

Рис.3.17

озглянемо випадок, коли точка А знаходиться на великій відстані від центра диполя порівняно із модулем плеча диполя ( рис. 3.17 ). В цьому випадку можна вважати, що ; ; , тоді можна використати наближені формули

, . (3.93)

Підставимо (3.93) в формулу (3.92)

. (3.94)

§ 3.6. Провідники в електричному полі. Електроємність відокремленого провідника

Провідниками називаються тіла, які мають вільні електричні заряди, тобто такі заряджені частинки, які можуть вільно переміщатись по об’єму провідника. Розглянемо для прикладу металевий провідник, в якому вільними зарядами є електрони. Кожен електрон має негативний електричний заряд, модуль якого рівний елементарному зарядові.

Вмістимо провідник в електричне поле. На рис. 3.18 провідник вміщений в однорідне зовнішнє-електричне поле. Під дією зовнішнього поля з напруженістю електрони в провіднику будуть переміщатись в напрямку, протилежному до напрямку поля , внаслідок чого в провіднику виникне внутрішнє електричне поле , протилежне за напрямком до зовнішнього. Переміщення електронів буде продовжуватись до тих пір, поки внутрішнє поле повністю не зкомпенсує зовнішнє. При цьому напруженість результуючого електричного поля всередині провідника стане рівною нулеві. Таким чином, зовнішнє електричне поле не може проникнути всередину провідника. Тобто електричне поле всередині провідника завжди відсутнє. Це стосується і того випадку, коли всередині провідника є порожнини.

Я

Рис.3.18

вище виникнення в провіднику внутрішнього електричного поля, рівного за величиною і протилежного за напрямком до зовнішнього, називається електростатичною індукцією. Це явище використовується для захисту електронних приладів та інших об’єктів від впливу зовнішнього електричного поля. З цією метою електричний прилад вміщують в замкнену металеву оболонку, яку, як правило, заземлюють. Такий метод захисту називається електростатичним захистом.

Слід зазначити, що явище електростатичної індукції в повній мірі стосується лише постійного, тобто статичного електричного поля. Змінне електричне поле частково може проникати вглиб провідника.

На основі формули (3.82) можна встановити зв’язок між потенціалом і напруженістю електричного поля

Оскільки всередині провідника , то , а отже .

Таким чином, потенціал електричного поля всередині провідника і на його поверхні є постійною величиною, а сама поверхня провідника є еквіпотенціальною. Силові лінії електричного поля завжди перпендикулярні до еквіпотенціальних поверхонь. Внаслідок цього силові лінії зовнішнього електричного поля біля провідника викривляються таким чином, що стають перпендикулярними до поверхні провідника як зображено на рис. 3.18. Ця властивість провідників використовується для створення електричних полів потрібної конфігурації за допомогою провідників спеціальної форми в електронних лампах, електронно-променевих трубках, електронних мікроскопах. В цих електронних приладах за допомогою провідників спеціальної форми (електродів) створюють елементи електронної оптики – електронні лінзи, дзеркала, призми.

Надамо деякому відокремленому провідникові заряду . Цей заряд розподілиться по поверхні провідника таким чином, що потенціал всіх точок поверхні і об’єму стане рівним . Напруженість електричного поля всередині провідника дорівнюватиме нулеві. Експериментально встановлено, що між величиною електричного заряду і потенціалом поверхні провідника існує пряма пропорційна залежність

. (3.95)

Величина називається електричною ємністю провідника або електроємністю.

. (3.96)

Електроємністю відокремленого провідника називається фізична величина рівна зарядові, який необхідно надати провідникові, щоб змінити його потенціал на одиницю. Електроємність залежить від форми, розмірів провідника, діелектричної проникності оточуючого середовища і не залежить від матеріалу провідника, його агрегатного стану, наявності в провіднику порожнин.

Одиницею вимірювання електроємності в системі одиниць є 1Фарад. 1Фарад – це електроємність такого провідника, потенціал якого змінюється на 1В при зміні його заряду на 1Кл.

Визначимо електроємність провідника у формі кулі радіусом . Надамо йому електричного заряду . Приймемо у формулі (3.88) що для поверхні кулі і , а для іншої точки, яку віддалимо на нескінченно велику відстань (), потенціал приймемо рівним нулеві . Таким чином, із виразу (3.88) отримаємо формулу потенціалу поверхні зарядженої кулі.

. (3.97)

Підставимо (3.97) у формулу (3.96) і отримаємо формулу електроємності кулі

. (3.98)