78 Явная и неявная двухслойная четырехслойная разностная схема для уравнения теплопроводности. Условия устойчивости

Рассмотрим уравнение теплопроводности

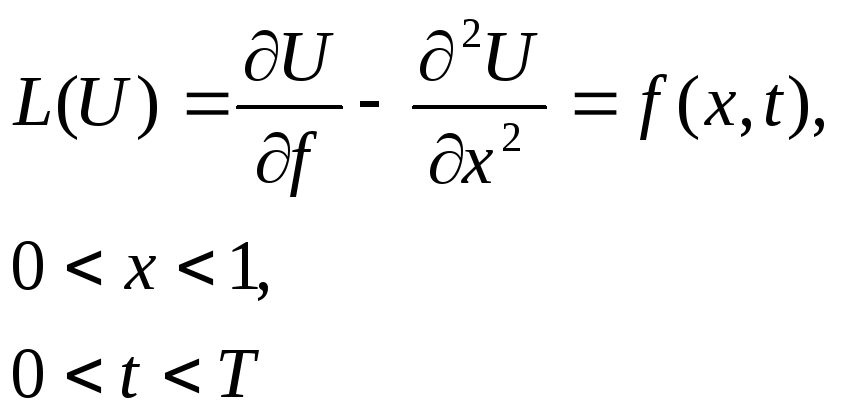
- начальное условие

- граничные условия

Предположим, что U(x,t) ! и - достаточно гладкие.

Пусть:

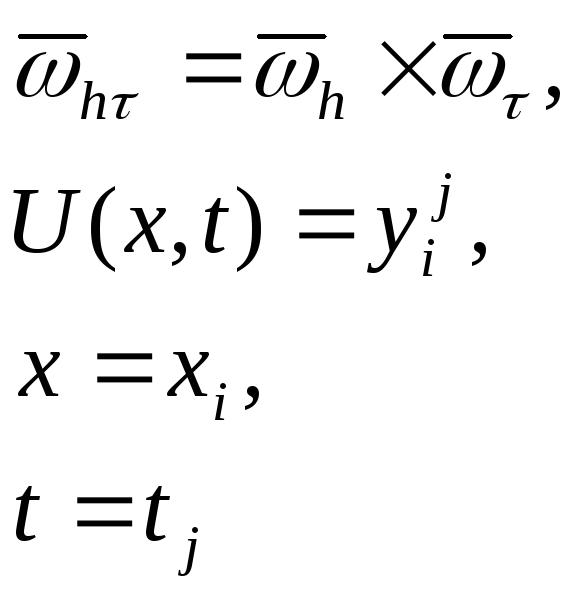
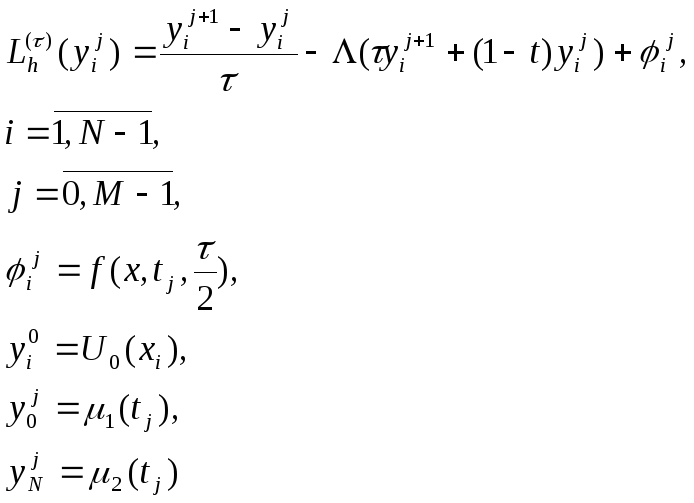
- точное решение на сетке

- решение разностной схемы

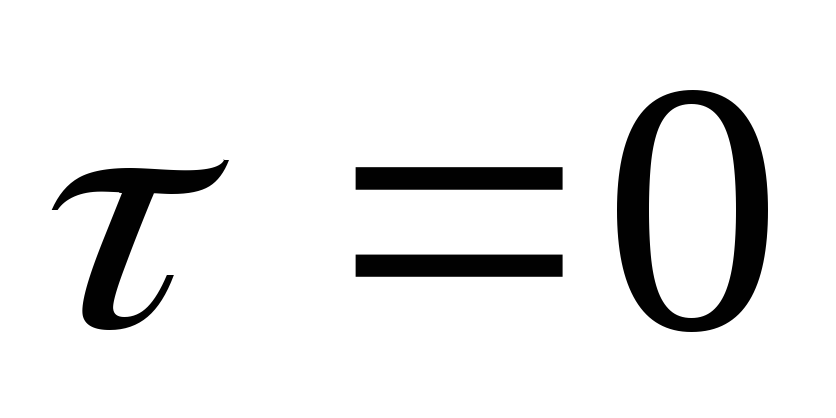
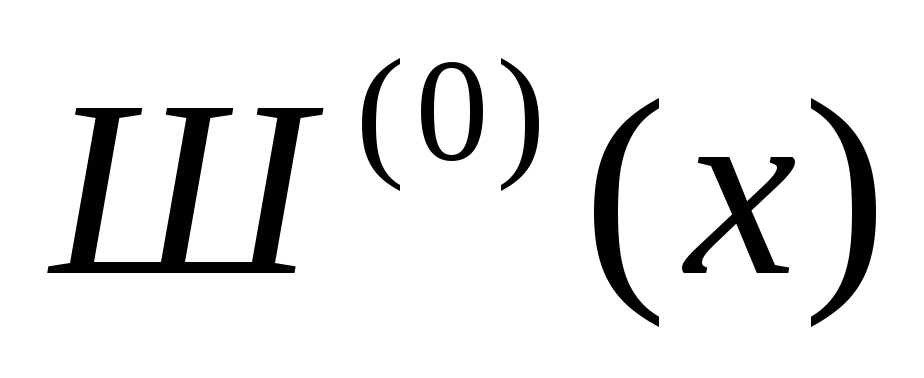
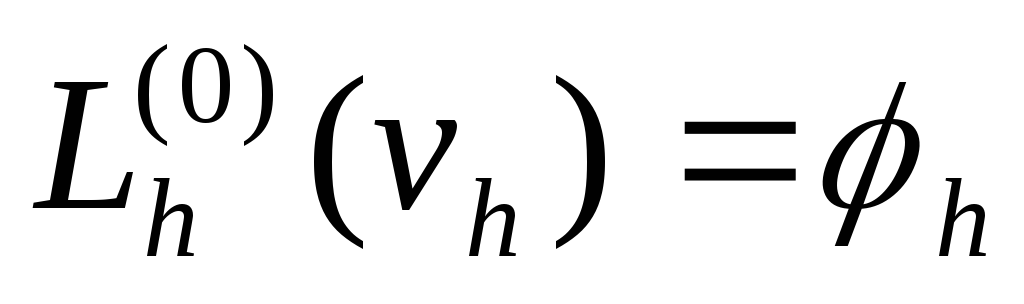
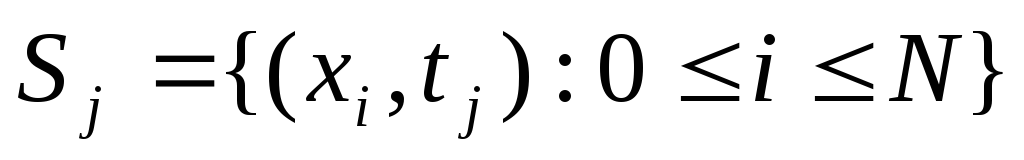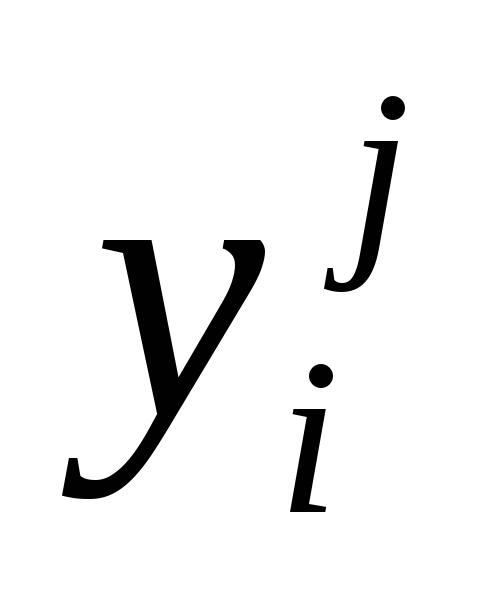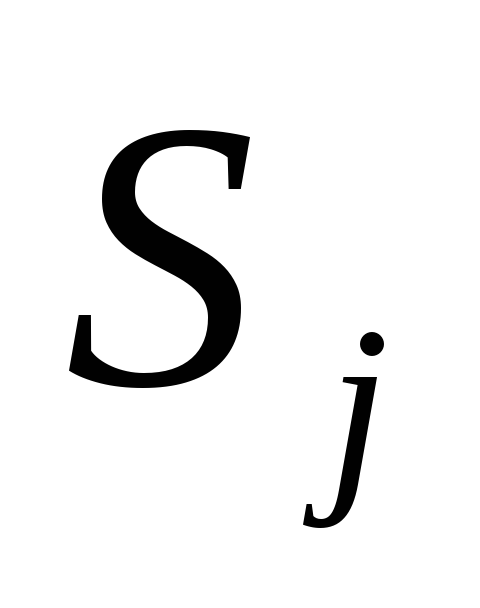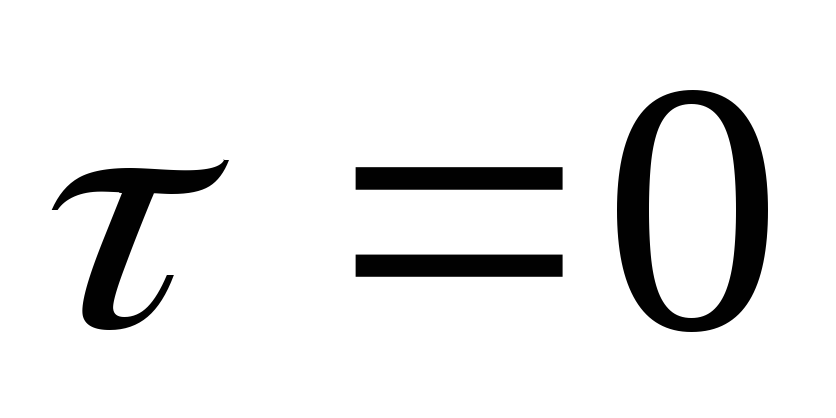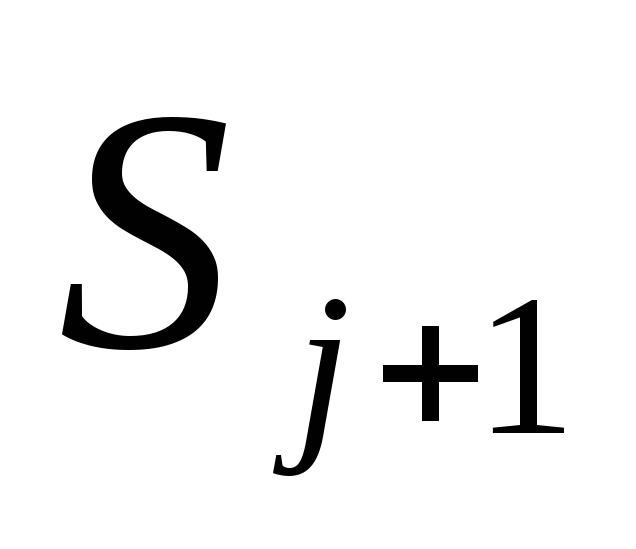1. - слой S(y)={-значения y на } Разностная схема при называется явной т.к. она позволяет явно вычислить значения на слое по значениям на .

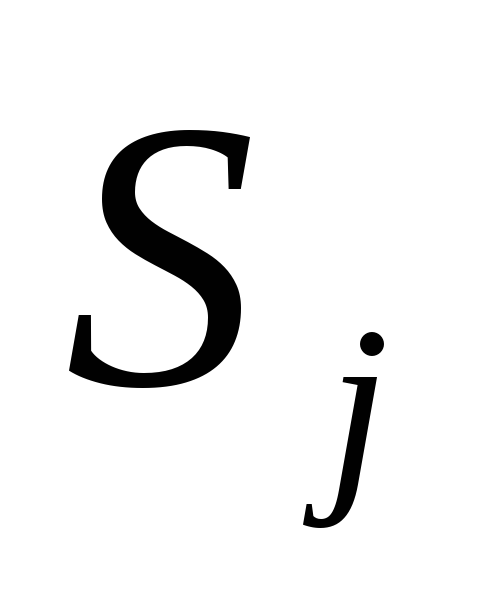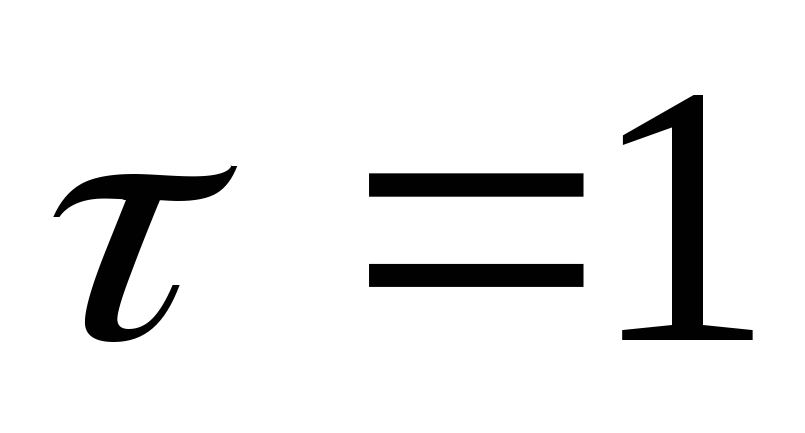
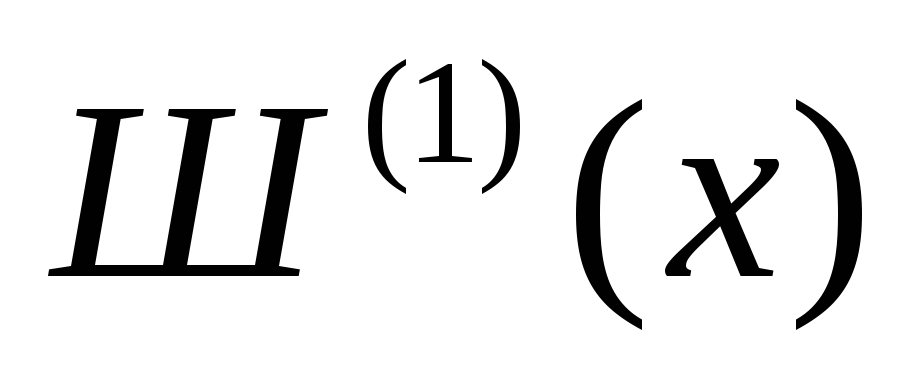2. Разностная схема 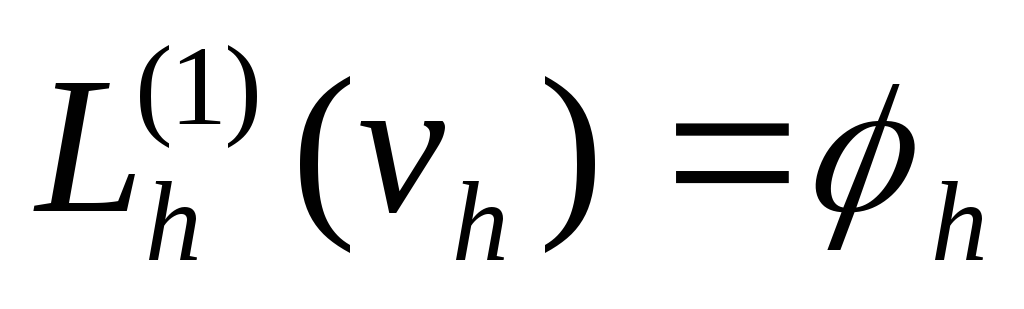Схема называется неявной, т.е. для вычисления решения на слое 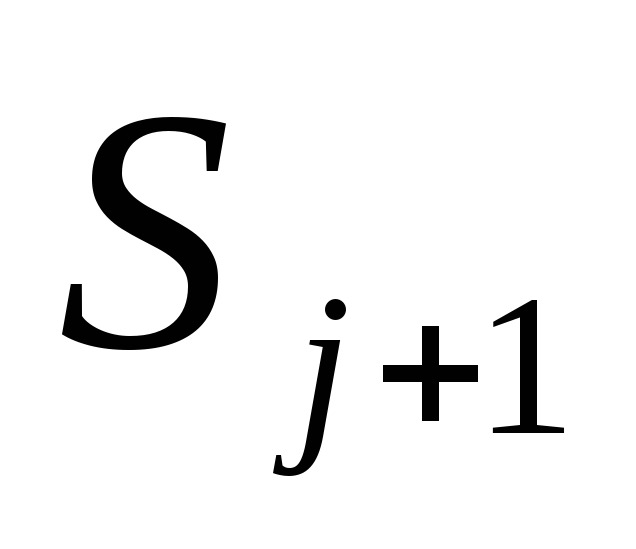по значениям на 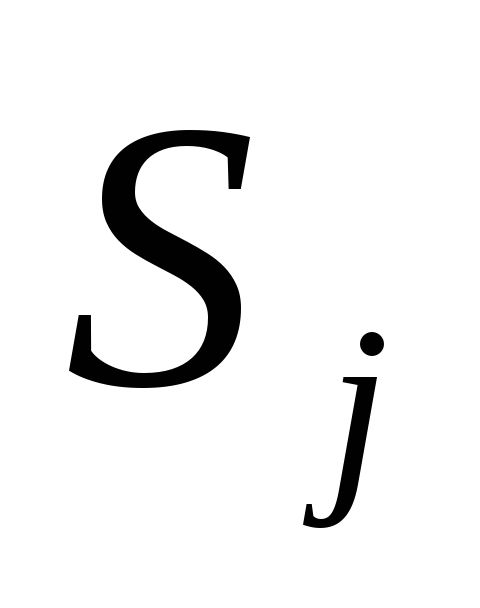необходимо решать СЛАУ.

Т устойчивость

Рассмотрим разностную схему .

Если разностная схема устойчива по начальным условиям в и верно: -решение разностной схемы.

79 Алгебра высказываний. Формулы. Равносильность формул. Функции алгебры высказываний. Способы заданий. Проблема минимизации.

Пусть задан алфавит

Выражение – конечная последовательность из алфавита.

Формула

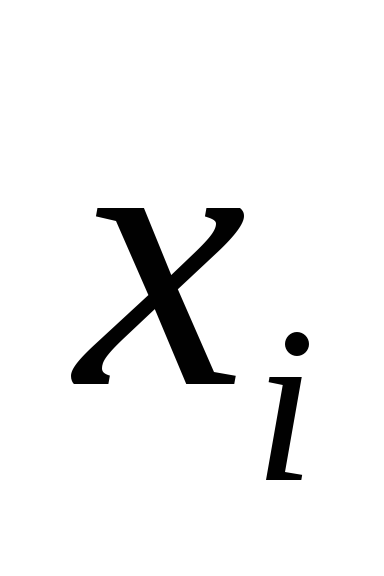1. - формула (высказывание).

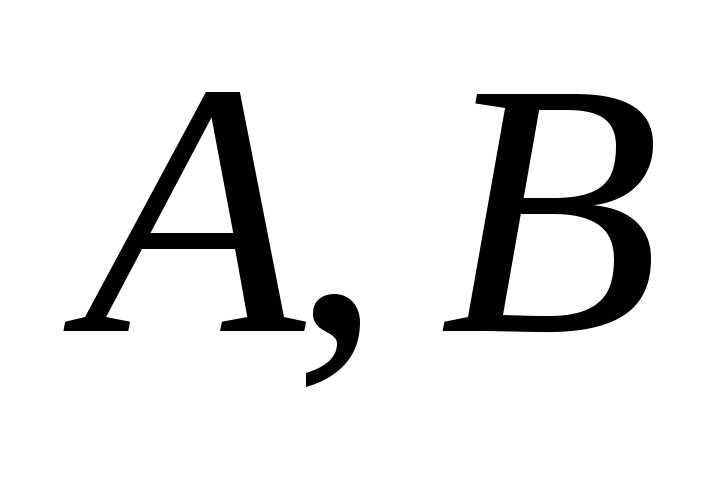2. - выражения которые являются формулами 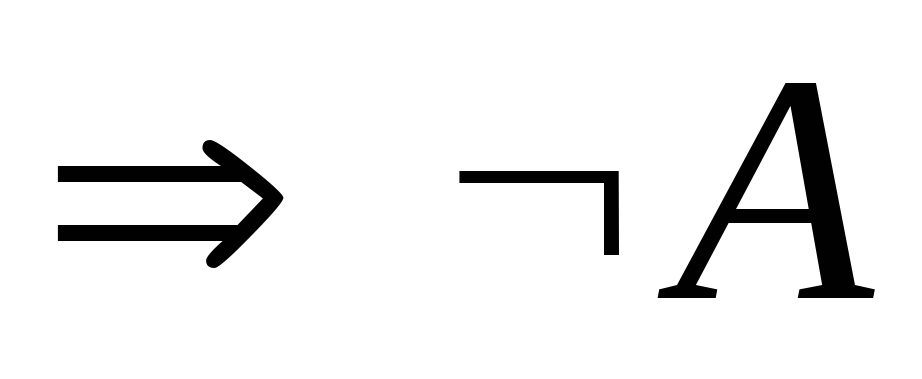и - формулы где

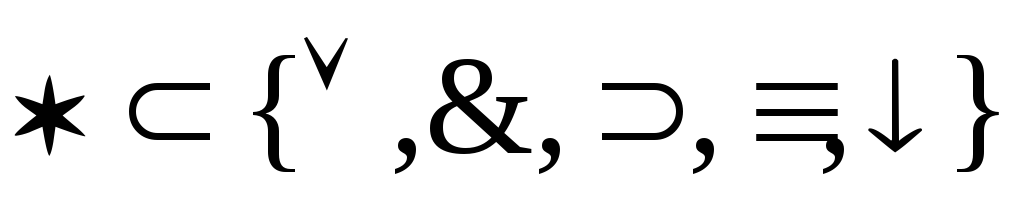
Алгебра высказываний – совокупность всех формул(высказываний). Каждой формуле ставится в соответствие функция .

Функции задаются таблицами истинности.

Опр. Функции называются равными, если они отличаются только фиктивными переменными: Заданы, , если :

.

Опр. Формулы равносильны, то есть если .

Проблема минимизации булевых функций – проблема построения их ДНФ.

80 Исчисления высказываний. Формулы, аксиомы, правила вывода. Вывод из гипотез. Теорема дедукции. Теорема о непротиворечивости исчисления высказываний. Независимость системы аксиом.

Исчисление высказываний – формальная аксиоматическая теорема логики высказываний.

Основные аксиомы:

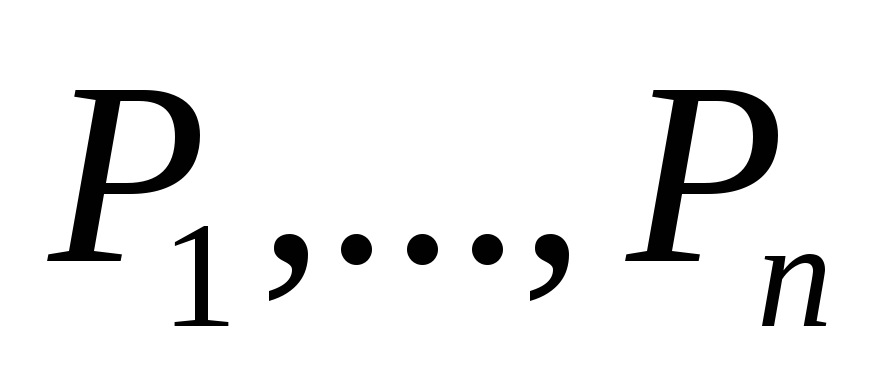1. - произвольные буквы(~ формулы)

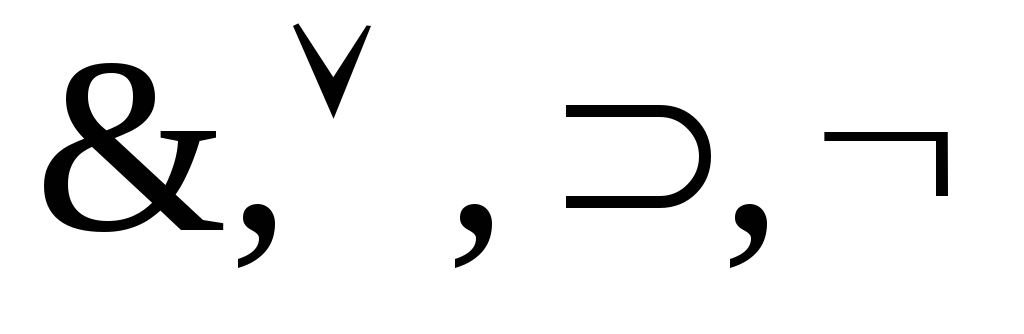2. - логические связки

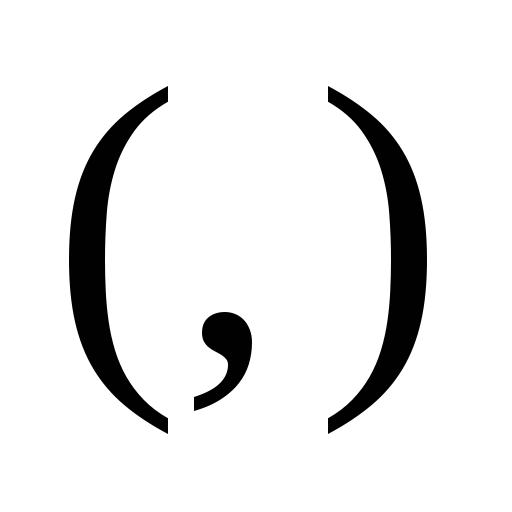3. - скобки

- формулы - формулы

То есть формулы определяются индуктивно.

Некоторые из формул теории называют аксиомами

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

Правила вывода:

1. modus ponens (MP)

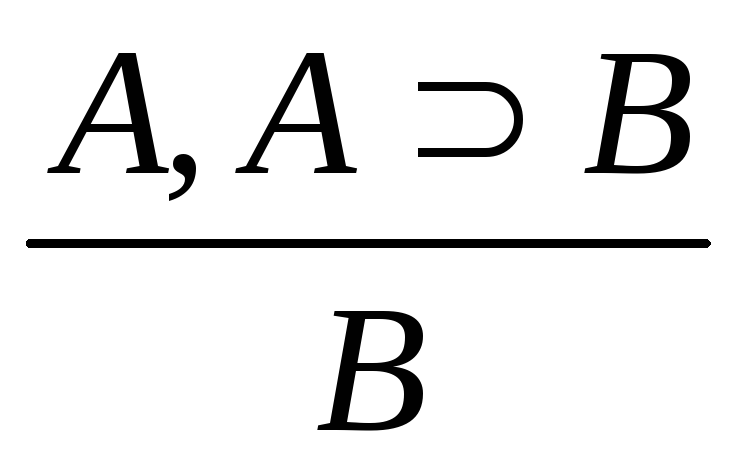
2. правило подстановки (S)

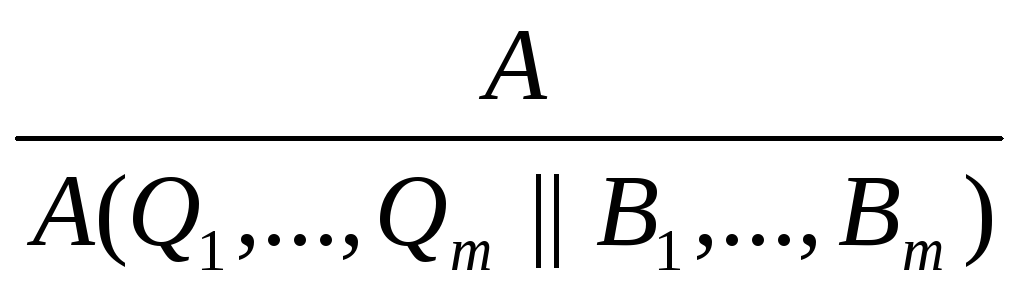
Теорема – выводимая формула.

Вывод – любая конечная последовательность формул , что каждая формула этой последовательности либо аксиома, либо совп. С пред., либо получена по правилам вывода из предыдущих.

Вывод - является выводом , а называется выводимой и обозначается .

Теорема (дедукции)

, тогда

Опр.

Аксиоматическая теория называется непротиворечивой, если ни для какого утверждения A этой теории, само A и не могут быть одновременно выполнимы.

Теорема (о непротиворечивости)

Исчисление высказываний есть непротиворечивая аксиоматическая теория.

Доказательство

Пусть F и одновременно выполнимы, но тогда F является тавтологией(Fистинная при любом подстановке любых конкретных высказываний) но тоже самое верно и для , а это невозможно по определению тавтологии.

Опр

Аксиома A из суммы аксиом называется независящей от остальных аксиом этой суммы, если ее нельзя вывести из множества всех остальных аксиом