51.Неравенства Гельдера, Минковского. Пространства Lp(t, μ), полнота.

Рассм меру -адд, полукольцо, конечную мн-во измеримых множест

Опр: измерима, если

- измеримо

Через обозначим мн-во измеримых ф-ий, для которых интеграл

Зададим стандартное отн эквивалентности:

Мн-во классов эквивалентных между собой ф-ий

обозначим . На этом мн-ве зададим метрику

является нормой, т.е. выполняются аксиомы нормы

1) , причем

2)

3) по нер-ву Минковского:

Нер-во Гельдера:

,

При помощи этого нер-ва доказывается след Т.

Т - полное норм пр-во

52.Теорема Лебега о предельном переходе под знаком интеграла Лебега.

Т(Егорова)

, - измеримая: , тогда

и

Т(об абс непр интеграла)

Т Лебега

-измеримы, , где - интегр

- интегр и

Д-во

интегр т.к. измерима т.к является пределом измеримых

интегр т.к. переходя к пределу получаем что

По абст непр интеграла

и

и (по Т Егорова)

Т.о.

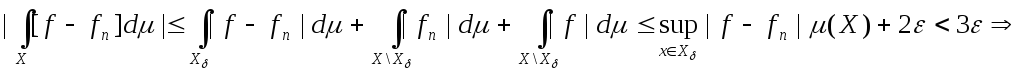ЧТД

53. Теорема Банаха (принцип сжимающих отображений).

Опр.

-неподвижная точка, если

Опр. -Липшицево, если

Если то называется сжимающим.

Т (Банаха)

В полном метрическом пр-ве сжимающее отобр. имеет 1 неподвижную точку.

Д-во

! Пусть

Аналогично для m>n

т.к. -п. Коши

Т.к. X-полное, то , значит

Т.о. , а f-непрерывно. Ч.т.д.

54.Линейные непрерывные операторы. Норма оператора. Примеры.

Опр. X, Y – векторные пространства над одним полем K. Отображение - линейный оператор, если :

1. ;

2.

.

Линейный оператор , где X и Y – нормированные пространства, называется ограниченным, если (1.) (нер-во ограниченности).

Теорема. X, Y –нормированные пространства, -линейный оператор. Следующие свойства эквивалентны :

1. A непрерывен в точке 0;

2. A непрерывен в любой точке;

3. A равномерно непрерывен;

4. A ограничен.

Опр. Норма линейного ограниченного оператора A – число , т.е. наименьшая из постоянных C , при которых справедливо неравенство ограниченности (1.).

Примеры.1. ;

A – линейный ограниченный оператор с нормой

2. - линейный, но не непрерывный

().

3. ; ; ; A – лин.непрерывный, .

4. - непрерывная функция, ; ; .

55.Теорема о замыкании образа линейного непрерывного оперетора.

X, Y – банаховы пространства, – ограниченный линейный оператор. Сопряженным оператором к A называется оператор , действующий по формуле . Он является линейным ограниченным оператором, причем .

Теорема. X, Y – банаховы пространства, – ограниченный линейный оператор. Замыкание образа оператора A есть множество векторов y, удовлетворяющих условию: для любого такого, что . (т. е. )

Д-во. Пусть – мн-во векторов , удовлетворяющих условию теоремы. L – замкнутое подпространство как пересечение замкнутых векторных подпространств. Пусть и . Тогда . Значит . Т.к. L замкнуто, то . Предположим , тогда по т. Хана-Банаха . Тогда и при значит, что . Противоречие. Теорема доказана

56. Теорема Хана-Банаха о продолжении функционалов.

Опр. Пусть -мно-во, -семейство отображений . Говорят, что это семейство разделяет точки пр-ва , если .

Можно показать, что для любого нормированного пр-ва мн-во всех линейных функционалов в сопряженном к нему пр-ве разделяет его точки.

Опр. -векторное пр-во. Полунорма на - отображение , удовлетворяющее условиям:

1. ;

2. ;

3. .

Теорема Хана-Банаха.

(действительный случай) Пусть -векторное пр-во над , -полунорма на ,-векторное подпр-во и на задан линейный функционал , удовлетворяющий условию . Тогда существует продолжение – линейный функционал такой, что и .

(комплексный случай) Пусть -векторное пр-во над , -полунорма на ,-векторное подпр-во и на задан линейный функционал , удовлетворяющий условию . Тогда существует продолжение – линейный функционал такой, что и .

Сл1. Пусть - точка нормированного пр-ва .Тогда существует линейный ограниченный функционал на такой, что и .

Сл2. Линейные ограниченные функционалы разделяют точки нормированного пр-ва , т.е.

Сл3. -векторное подпр-во нормированного пр-ва , - внешняя точка для . Тогда . (Если - замкнутое векторное подпр-во в , то условие -внешняя точка эквивалентно условию ).