- •С использованием смещения
- •При изменении разрядности числа () требуется пересчет числа
- •С использованием двоично-дополнительного кода
- •С отрицательным показателем
- •Симметричная
- •Кодирование двоичных потоков
- •Внутреннее представление вещественных чисел
- •С фиксированной точкой
- •С плавающей точкой
- •Денормализованные вещественные числа
- •Преобразование десятичного числа в двоичное представление
- •Перевод числа в двоичную систему
- •Нормализация – разложение на мантиссу и экспоненту основания (2) системы счисления
- •Вычисление конечной экспоненты числа (т.Е. Характеристики)
- •Корректировка мантиссы числа
- •Запись результата
- •Округление вещественных чисел
- •Ссылки по теме
Введение в программирование и ЭВМ
|
|
|
|
|
ИТМО, ФИТИП, КТ
Скаков Павел Сергеевич
|
|
[Введение в программирование и ЭВМ] |
|
Сборник лекций, читаемых автором Скаковым Павлом Сергеевичем на кафедре КТ, НИУ ИТМО. Составил по памяти и немного дополнил – Лукьянов Алексей, студент группы 1537 КТ в 1семестре 2011. |
Лекция 1. Системы счисления и внутреннее представление чисел
От 01.09.2011
Системы счисления
Шестнадцатеричная система счисления полезна при представлении двоичных чисел. Обозначается 0x1AFили 1AFh, где 1AF – шестнадцатеричное число.
Конечная или периодическая дробь при переводе в другую систему счисления всегда также переводится в конечную или периодическую дробь.
Октет – блок из 8 бит. Дело в том, что байт не на всех архитектурах равен 8 битам.
Внутреннее представление целых чисел
Способы представления двоичных чисел со знаком, основные способы:
-
С использованием 1 бита под знак
Первый бит – знак числа, причем 0 соответствует положительному числу, 1 – отрицательному. Т.о. положительное число не меняет традиционного представления. Остальные же биты всегда представляют положительное число, вне зависимости от знака.
Минусы:
-
Два нуля – положительный и отрицательный – усложняют работу с такими числами
-
По-разному реализуются сложение и вычитание
-
На значение меньше, чем в двух других способах
-
При изменении разрядности числа (
 )
требуется пересчет числа
)
требуется пересчет числа
-
С использованием смещения
Суть
в том, что для получения внутреннего
представления числа требуется прибавить
к числу некоторое смещение
– другое число, константа, обычно
половина (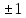 )
от максимального значения. И наоборот,
если вычесть из внутреннего представления
смещение, то получается итоговое
число-значение. Т.о. если октет содержит
значение 200 а смещение данной архитектуры
равно 127, то число, содержащееся в этом
октете – это 73. Если содержит 0, то
)
от максимального значения. И наоборот,
если вычесть из внутреннего представления
смещение, то получается итоговое
число-значение. Т.о. если октет содержит
значение 200 а смещение данной архитектуры
равно 127, то число, содержащееся в этом
октете – это 73. Если содержит 0, то
 и т.д.
и т.д.
Минусы:
-
После каждой операции над числами нужна коррекция, что тормозит работу
-
При изменении разрядности числа () требуется пересчет числа
-
С использованием двоично-дополнительного кода

Прочие способы (представляют только академический интерес, т.к. слишком неэффективны):
-
С отрицательным показателем
Т.е. значение битов не 128, 64, 32, …, 2, 1, а -128, 64, -32, …, -2, 1. Такой способ позволяет представить все числа в определенном диапазоне, не образуя «дыр».
Минусы:
-
Неравномерное распределение положительных и отрицательных чисел
-
Симметричная
Может быть реализована только для систем счисления с нечетным основанием. Использовалась в одной из советских разработок в троичной системе счисления.
Отличительная особенность в том, что каждый разряд кроме нуля заключает в себе знак. Т.о. разряд может принимать значение 0, 1..nи (-1)..(-n), где n– предельное значение разряда.Причем отрицательные значения записываются в виде букв латинского алфавита, начиная с его конца (z, y, x, …).
Важное замечание: при переносе значения в старший разряд, данный разряд принимает не значение 0, как обычно, а меньшее значение, которое он только способен принять.
Пример:
троичная симметричная система. Значение
каждого разряда может быть следующим:
1, 0, z, где
 .
Показатели разрядов в этом случае будут:
27, 9, 3, 1.
.
Показатели разрядов в этом случае будут:
27, 9, 3, 1.
Разряды могут принимать значение:
3: (-27,0,27)
2: (-9,0,9)
1: (-3,0,3)
0: (-1,0,1)
Представление чисел:
-2 = z1
-1 = z
0 = 0
1 = 1
2 = 1z
3 = 10
4 = 11
5 = 1zz
6 = 1z0
7 = 1z1
Примеры отраслевого применения:
-
Кодирование двоичных потоков
0: 0
1: -1
10:3
11:-9
…
Внутреннее представление вещественных чисел
-
С фиксированной точкой
Например, число 5.1 равно:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |

Последний разряд установлен в 0, а предпоследний в 1 из-за округления.
Плюсы: работа с вещественными числами как с целыми – одно железо, просто и быстро
Минусы: фиксированная точность
-
С плавающей точкой
Вся вещественная арифметика с плавающей точкой интересна тем, что, во-первых, точности от нее ждать не приходится, а во-вторых, тем, что разными платформами стандарт поддерживается весьма избирательно. В одном аспекте может поддерживаться, а в другом – нет. Такая вот занимательная арифметика.
В этом представлении число разбивается на знак, мантиссу и экспоненту. Знак неизменно занимает один старший бит, размер остальных частей зависит от формата.
Существуют следующие форматы (стандарт IEEE754):
|
Название |
Знак |
Мантисса |
Экспонента |
Всего бит |
Первый бит |
||
|
Half |
1 |
10 |
5 |
16 |
Нет |
||
|
Single |
1 |
23 |
8 |
32 |
Нет |
||
|
Double |
1 |
52 |
11 |
64 |
Нет |
||
|
Quad |
Все вместе 128 бит, редко используется |
128 |
Нет |
||||
|
Extended |
1 |
64 |
15 |
80 |
да |
||
Существует оригинальный формат extended, в котором сопроцессор выполняет все вычисления и все остальные форматы, используемые только для сжатия данных.
При переводе числа в двоичную систему счисления первый бит всегда будет равен единице, поэтому во всех форматах, предназначенных для сжатия данных, этот бит отсутствует, но подразумевается. Формат extended – полное представление числа, поэтому в нем первый бит стоит на своем месте, он необходим для вычислений.
Не все архитектуры поддерживают стандарт полностью. Например, видеокарты упрощают вычисления, снижая их точность для повышения быстродействия.