Закон Архимеда

Н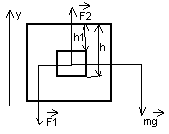 а тело погружённое в жидкость или газ действует сила равнодействующая весу вытесняемой данным телом жидкости или газа. Данная сила будет действовать в том случае если жидкость или газ со всех сторон охватывает данное тело.

F2+F1+mg=0

Y:F2=-rжg*h*S+rж*g*h1*S-r*g(h-h1) =0

rж- плотность жидкости; r - плотность тела; S – площадь верхней и нижней поверхностей тела.

r*g*S(h1-h)= r*g(h-h1)S

Величина стоящая в левой части уравнения определяет выталкивающую силу (Архимедову) действующую на тело. Величина стоящая в правой части определяет вес тела. Таким образом на тело покоящееся в жидкости или газе действует статическая выталкивающая сила получившая название архимедовой.

Уравнение непрерывности сплошности

Движение масс жидкости или газа удобно изобразить в виде линий тока. С помощью данных линий можно определить как направление движения жидкости или газа так и скорость (изменения) той или иной части трабки тока. Направление движения определяется с помощью стрелок линий тока. Величина скорости определяется с помощью густоты линий тока, чем гуще лини тока тем больше скорость в данной области трубки тока. Уравнение непрерывности сплошности справедливо в случае идеальной не сжимаемой жидкости. Рассмотрим некоторую трубку тока. В сечении S1 в данной трубке тока жидкость протекает со скоростью V1, а в сечении S2 протекает со скоростью V2. Сколько линий вошло через первое сечение столько выйдет и через второе поэтому справедливо равенство.

Для несжимаемой жидкости VS=const

Введём понятие элементарного потока, поток используется не только для описания течения жидкости, но и для описания векторных полей любой иной природы. В том случае если имеется ток жидкости в некоторой области пространства и жидкость протекает со скоростью V, то можно утверждать, что в данной области пространства задано векторное поле вектора V. Выберем некоторую элементарную площадку dS.

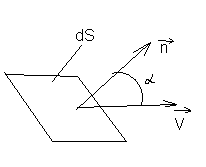
Через которую протекает данная жидкость со скоростью V и вычислим объём протекающий в единицу времени через данную площадку. Данный объём получил название элементарного потока вектора V через элементарную площадку dS. Данный элементарный поток может быть определён как

Α – угол между нормалью к данной элементарной площадке и вектором V. –вектор модуль которого равен dS, а направление совпадает с направлением вектора .

Для того что бы вычислить поток через поверхность площадью S необходимо сложить все элементарные потоки через данную поверхность. Реально суммирование сведётся к интегрированию по поверхности S.

В векторном анализе с помощью которого описывается гидродинамические процессы вводится понятие поток через замкнутую поверхность. Замкнутой называется поверхность в векторном анализе.

Замкнутая поверхность S это та которая содержит внутри себя объём V

В том случае если внутри некоторой замкнутой поверхности нет ни источников ни стоков жидкости то поток через данную замкнутую поверхность будет равно нулю.

Величину равную произведению плоскости жидкости на скорость можно определить как плотность потока жидкости.

ρ – плотность жидкости.

Предполагаем, что в некотором объеме V находится жидкость массой m и через поверхность S охватывает объем V данная масса жидкости вытекает

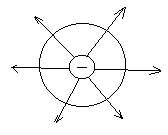
Скорость убывания данной массы жидкости может быть определена как

Из данного выражения которое описывает принцип непрерывности слпошности используя теорему Остроградского Гаусса можно получить уравнение непрерывности сплошности в дифференциальной форме.

где V находится внутри поверхности S.

Поток вектора j через замкнутую поверхность S равен объемному интегралу от дивигенции вектора j по объёму V находящейся внутри данной поверхности объёмом S.

div – оператор векторного анализа который применяется к векторной функции и в результате его действия на векторную функцию получается скалярная функция.

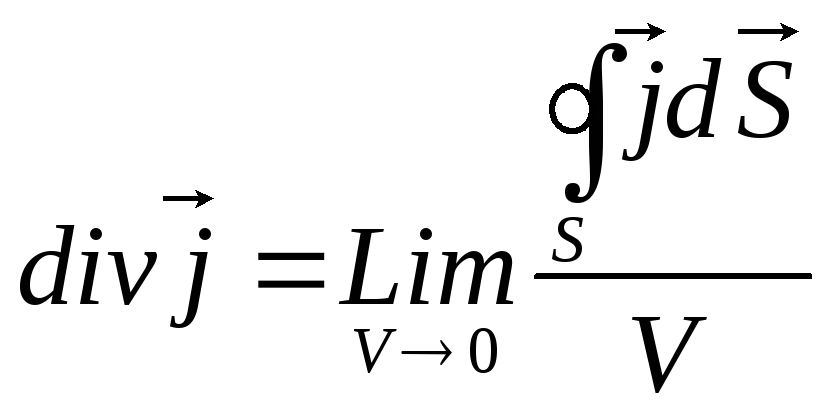
V – объём находящийся внутри замкнутой поверхности S.

Из теоремы следует, что: