
- •Механика
- •Кинематика
- •Кинематика вращательного движения
- •Динамика поступательного движения
- •3 Закон Ньютона: Тела взаимодействуют с силами равными по величине и противоположными по направлению. На основание третьего закона можно сравнивать лишь силы приложенные к разным телам.
- •Упругие силы
- •Деформация сдвига
- •Сила тяжести вес тела
- •Сила трения
- •Энергия работа мощность.
- •Мощность
- •Кинетическая энергия
- •Потенциальная энергия
- •Законы сохранения
- •Закон сохранения импульса
- •Уравнение движения тела с переменной массой (уравнение реактивного движения)
- •Закон сохранения энергии
- •Деформация (упругое тело)
- •Абсолютно упругие и не упругие удары
- •Закон сохранения момента импульса
- •Пример расчёта моментов инерции тела
- •Кинетическая энергия вращательного движения
- •Понятие о тензоре момента инерции
- •Свободные оси, гироскоп, гироскопический эффект.
- •Сущность гироскопического эффекта
- •Силы инерции (не инерциальные системы отсчёта)
- •Проявление в природе сил инерции
- •Элементы теории гравитационного поля
- •Понятие о космических скоростях
- •Элементы механики жидкости и газа
- •Закон Паскаля
- •Закон Архимеда
- •Уравнение непрерывности сплошности
- •Уравнение Бернулли.
- •Вязкость жидкости
- •Движение тел в жидкости или газе
- •Молекулярно кинетическая теория идеальных газов
- •Закон Дальтона
- •Основное уравнение молекулярно кинетической теории
- •Распределение Максвелла.
Деформация (упругое тело)
Предпологаем, что некоторое тел массой m находится на пружине жёсткостью к пружина растянута на max величину X0, таким образом тело в поле силы упругости обладает потенциальной энергией (кx²)/2, пружина начинает сокращаться и тело начинает двигаться вверх при этом при этом приобретает скорость V, следовательно в некоторый момент времени тело будет обладать кинетической энергией и эта энергия может быть определена как:
Т=Е-Пx
Где: Пх – потенциальная энергия тела в поле упругой силы в той точке где тело имеет кинетическую энергию Т.
Т=П-Пх
Где: х – абсолютное удлиннение пружины.
![]()
Кинетическую энергию можно определить и графически, построить график потенциальной энерги о X и определить потенциальную энергию в точке X.
![]()

Рассмотрим зависимость потенциальной энергии от координат. Предпологаем что зависимость потенциальной энергии некоторого тела в поле консервативных сил выглядит так как показано на рисунке. Е – полная механическая энергия системы. Выделим три характерные области 1, 2, 3. В област 2 тело находиться не может так как потенциальная энергия тела превосходит полную механическую энергию тела и следовательно и следовательно кинетическая энергия тела дорлжна быть отрицательной. Для того что бы телу перейти из области 1 в область 3 ему необходимо преодолеть потенциальный барьер высотой Пmax что тело может сделать если ему сообщить дополнительную энергию равную разности Пmax-E.
В класической механике: тело обладает энергией ЕПmax и преодолеть потенциальный барьер преодолеть не может.
В квантовой механике: частица обладающая энергией ЕПmax может преодолеть потенциальный барьер как бы пройдя по тонелю в нутри данного барьера.
Таким образом при заданном соотношении потенциальной энергии и полной механической энергии частица (тело) может двигаться лишь внутри области 1. Частица находится внутри потенциальной ямы шириной L глубиной П1.
Абсолютно упругие и не упругие удары
Ударом называется кратковременное взаимодействие двух или более тел. При ударе возникают столь значительные внутренние силы взаимодействия тел, что данные силы превосходят по величине внешние силы действующие на систему, а поэтому систему соударяющихся тел можно считать замкнутой. Сущность удара заключается в преобразовании кинетической энергии относительно движения соударяющихся тел в энергию упругой деформации тел при этом в процессе удара происходит перераспределение энергии между соударяющимися телами. Реально для ударов всегда выполняется соотношение V’V где V’ – относительная скорость соударения тел после удара. V – до удара. ИЭто объясняется тем что в реальной ситуации часть полной механической энергии переходит в энергию тепловую.
=V’/V – коэфициент восстановления.
Для реальных ударов величина 1. Предельными являются случаи =0 и =1. В случае когда величина =0 имеем абсолютно не упругий удар (АНУ). =1 – соответствует случаю абсолютно упркгого удара (АУУ). Характерной чертой АНУ является то, что тела после соударения движутся вместе как одно целое. Примером удара близкого к абсолютно не упрукгому удару является движение двух пластилиновых шаров. Характерной чертой АУУ является то что после соударения в общем случае тела движутся в разные стороны с различными скоростями. При АУУ после соударения не остаётся ни каких остаточных деформаций соударяющихся тел и все кинетические энергии системы до удара преобразуются в кинетические энергии после удара. Это объясняется тем что внутренне силы возникающие в процессе соударения при АУУ по своей природе близки силам упругости, а поэтому система является консервативной (или потенциальной) . Для потенциальной системы выполняется закон сохранения механической энергии.
Рассмотрим пример АУУ на случае соударения двух шаров движущихся в одном направлени с различными скоростями.
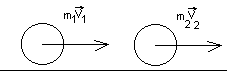
П осле
соударения мела движутся со скоростью
V1’ и V2’
соответственно.
осле
соударения мела движутся со скоростью
V1’ и V2’
соответственно.
Для описания движеничя шаров применим закон сохранения импулься (система является замкнутой так как внутринние силы значительно превосходят внешние силы), а также закон сохранения механической энергии.
Суммарный импульс системы за бесконечно малый прмежуток времени до удара равен суммарному импульсу системы через бесконечно малый промежуток времени после удара.
m1V1+m2V2=m1V1’+m2V2’
Так как система является консервативной то для неё можно применить закон сохранения энергии.
=
где: =Т2-Т1=![]()
- изменение кинетической энергии в процессе удара. Т2– кинетическая энергия системы после удара. Т1 – кинетическая энергия системы до удара.
Так как в поле консервативных сил тела за малый промежуток времени не меняют в процессе удара своего положения поэтому (иэменение потенциальной энергии равно нулю). Отсюда следует что закон сохранения механической энергии преобразуется в закон сохранения энергии кинетической. Таким образом исходя из закона сохранения импульса и закона сохранения механической энергии получилась следующая система:

![]()

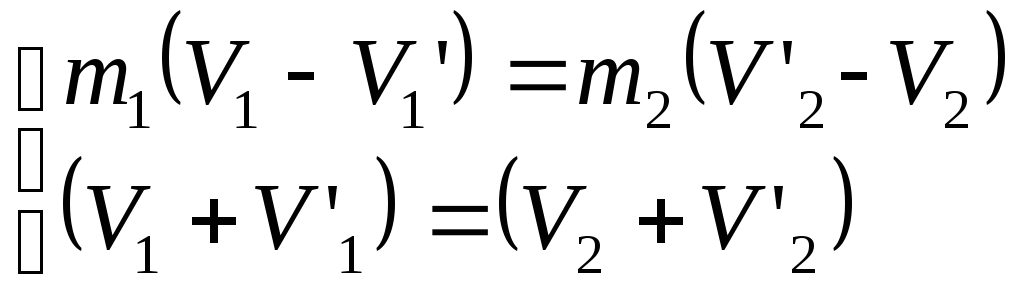
Решая полученную систему двух уравнений относительно двух неизвестных получаем выражение скорости первого и второго шара после удара:

АНУ
При АНУ в прцессе соударения возникают внутринние силы которые по своей природе близки к силам трения поэтому в процессе удара система является не консервативной и следовательно для данной системы не выполняется закон сохранения механической энергии, но выполняется закон сохранения полной энергии. Часть механической энерги переходит в иные виды энергии например тепловую.
Рассмотрим пример АНУ в случае взаимодействия двух тем с массами m1 и m2 которые движутся в одном направлении причём первое со скоростью V1 а второе со скоростью V2. Так как внутринние силы значительно больше внешних сил система является замкнутой и для неё применим закон сохранения импульса.
m1V1+m2V2=(m1+m2)V
где: V – скорость соударения тел после удара
![]()
В том случае если шары будут двигаться на встречу друг другу, то закон сохранения импульса в векторном виде при m1m2 может быть записан так:
![]()
![]()
где: К0 – единичный вектор направленный вдоль скорости V1.
![]()
Определим ту часть механической энергии которая в процессе соударения переходит в другие виды энергии. Данная часть полной механической энергии которая переходит в иные виды энергии определяется для случая движения шаров в одном направлении.
Q=T=Т2-Т1
T – изменение кинетической энергии системы в процессе соударения. Т2 – кинетическая энергия после удара Т1 – кинетическая энергия до удара.

Знак минус говорит о том что кинетическая энергия до удара переходит в кинетическую энергию после удара.
Ранее были рассмотрены случаи центрального удара то есть удара при котором скорость соударения тел до удара направлена по прямой соединяющей их центры масс. Реально в природе наблюдаются и не центральные удары, то есть такие удары у которых вектора скорости не лежат на одной прямой. В этом случае исследование такого вида движения производится по такой же методике как и в случае центрального удара, но необходимо при записании законов произвести проецирование векторов скорости на координатные оси предварительно выбранной системы отсчёта и записать уравнение законов сохранения импульса и энергии в проекции на данные оси.
