МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

"МАТИ" - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

им. К.Э. ЦИОЛКОВСКОГО

В.С. АКИНЬШИН, Ю.В. ГРУЗДЕВ, М.В. РЫЛЬСКАЯ

ФИЗИЧЕСКИЙ ПРАКТИКУМ. МЕХАНИКА

Учебное пособие

Утверждено Учебно-методическим советом университета в качестве учебного пособия для студентов всех специальностей

Москва 2003

Виктор Сергеевич Акиньшин

Юрий Викторович Груздев

Мария Владимировна Рыльская

ФИЗИЧЕСКИЙ ПРАКТИКУМ. МЕХАНИКА

Учебное пособие

Компьютерная верстка О.В. Чибисова

Редактор М.А. Соколова

Подп. в печ. 17.11.03 Объём усл. печ. л. 6,2 Тираж 100 экз. Уч. изд. 17,6

Заказ №229

Издательский центр

МАТИ" - Российского государственного технологического

университета им. К.Э. Циолковского, Берниковская наб. 14

Предисловие

Учебное пособие состоит из трех глав и Приложения. Первая глава носит вводный характер. В ней рассмотрены основные виды погрешностей измерения и даны рекомендации по обработке результатов эксперимента. Вторая и третья главы содержат руководства к 11 лабораторным работам цикла "Механика". Каждое руководство состоит из цели работы, теоретических основ физических явлений, наблюдаемых в работе, описания экспериментальной установки, а также подробного описания последовательности действий при проведении эксперимента. Кроме того, к каждой работе даны 30 контрольных вопросов для самоконтроля студента. В Приложении приведена таблица коэффициентов, позволяющих вычислять полуширину доверительного интервала (абсолютную погрешность) измеряемой величины.

Руководства к лабораторным работам №№ 4, 8, 10, 11 написаны В.С. Акиньшиным; глава 1 и руководства к работам №№ 1, 2, 3, 5, 6, 7 написаны Ю.В. Груздевым; руководство к работе № 9 написано М.В. Рыльской.

Авторы выражают глубокую благодарность всем преподавателям и сотрудникам кафедры "Физика", участвовавшим в обсуждении методики лабораторных работ цикла "Механика" и в подготовке экспериментальных установок, особо отмечая выдающийся вклад инженера Б.В. Зверлова в работу по постановке экспериментов.

Глава I. Основы обработки результатов эксперимента измерения и погрешности измерений

В каждой лабораторной работе по курсу "Физика" студент измеряет одну или несколько величин. Измерение называется прямым, если измеряемая величина непосредственно сравнивается с эталоном. Такое сравнение, как правило, происходит с помощью измерительного прибора. Например, длина тела измеряется с помощью микрометра или штангенциркуля, сила тока измеряется амперметром и т.д. Результат косвенного измерения является известной функцией величин, получаемых с помощью прямых измерений. В процессе прямого измерения получают ряд наблюдений х₁, х₂, … , х_n измеряемой величины х. Результаты отдельных наблюдений содержат погрешности измерений и нуждаются в дополнительной обработке. Виды погрешностей: случайные, систематические, промахи.

Случайные погрешности

При наличии случайных погрешностей результат отдельного наблюдения х_k измеряемой величины х является случайной величиной. В этом случае результаты наблюдений х₁, х₂, … , х_n одной и той же величины х различны. В качестве результата измерения принимается среднее арифметическое значение результатов наблюдений:

. (1.1)

Предел результата измерения при n называется математическим ожиданием :

. (1.2)

Случайную величину х, являющуюся результатом отдельного наблюдения, можно задать с помощью функции распределения f(х) (функции плотности вероятности):

или , (1.3)

где dP - вероятность попадания случайной величины в интервал (х, х+dx) шириной dx.

Если случайная величина зависит от большого количества неконтролируемых изменяющихся причин, то она подчиняется нормальному распределению или распределению Гаусса. Функция распределения Гаусса для случайной величины х с математическим ожиданием  описывается формулой:

, (1.4)

где - дисперсия распределения. Величина называется стандартным или среднеквадратичным отклонением. График функции распределения Гаусса показан на рис.1.

Математическое ожидание  определяет положение оси симметрии кривой распределения, а величина  характеризует разброс х относительно .

С учетом формулы (1.3) вероятность Р попадания результата наблюдения х в интервал (х₁, х₂) равна

Рассмотрим интервал, в центре которого находится математическое ожидание , а полуширина равна

, (1.5)

где - некоторое число. Вероятность Р наблюдения случайной величины х, подчиняющейся нормальному распределению, в таком интервале определяется формулой:

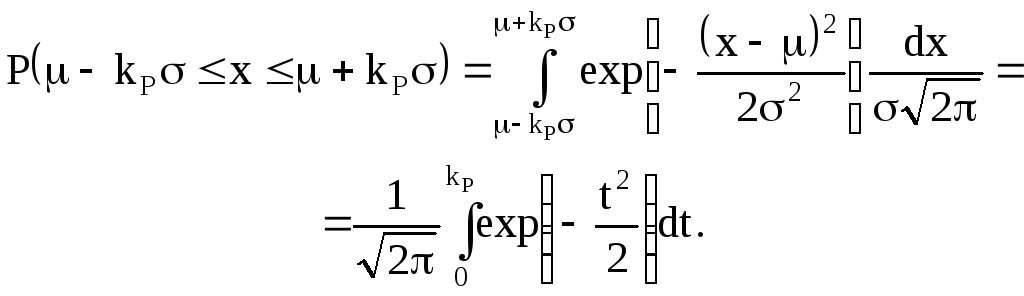(1.6)

Вычисление интеграла в формуле (1.6) показывает, что при k_P = 1,0 вероятность Р = 0,68, т.е. 68% результатов наблюдений лежат внутри интервала (). Соответственно, при k_P = 2,0 получим Р = 0,95, а при k_P = 3,0 вероятность Р = 0,997.

Пусть наличие случайных погрешностей приводит к тому, что результат наблюдения х измеряемой величины подчиняется нормальному распределению. Параметры  и  этого распределения экспериментатор не знает. В процессе измерения получают n результатов наблюдений: х₁, х₂, … , х_n, т.е. получают некоторую выборку значений х из генеральной совокупности допустимых значений. Определяя результат измерения по формуле (1.1), находят выборочную оценку величины . Выборочную оценку дисперсии нормального распределения результатов наблюдений получают по формуле

, (1.7)

где S(х) - выборочная оценка стандартного отклонения результата наблюдения; n - число наблюдений.

Если результат отдельного наблюдения х является случайной величиной, подчиняющейся нормальному распределению с дисперсией D(х), то результат измерения , определяемый по формуле (1.1), также подчиняется нормальному распределению с дисперсией . Соответственно, выборочная оценка стандартного отклонения результата измерения равна

. (1.8)

Теоретически показано, что для каждой вероятности Р (меры доверия) можно построить такой доверительный интервал (), что математическое ожидание  случайной величины х окажется внутри этого интервала с вероятностью Р. Полуширина такого доверительного интервала определяется формулой:

, (1.9)

где S() находим по формуле (1.8), а - коэффициент Стьюдента, величина которого зависит от вероятности Р и числа степеней свободы  (см. таблицу Приложения). Число степеней свободы  связано с числом наблюдений n формулой: . Можно показать, что в формуле (1.5) коэффициент

. (1.10)

При наличии только случайных погрешностей запись результата измерения: .