1.3.1 Гістограма і її побудова

Нехай є вибірка з n значень вимірюваної величини. Для того, щоб одержати перше уявлення про розподіл цієї величини будують так звану гістограму. Гістограма це ступінчастий графік (діаграма), для побудови якої по осі абсцис відкладають значення вимірюваної величини, розбиті на інтервали (біни), а по осі ординат - кількість Δn значень цієї величини, що потрапляють у кожен бін. По осі ординат можуть бути відкладені також імовірності Δn/n влучення обмірюваного значення в певний бін, при цьому вигляд гістограми не зміниться.

Для побудови гістограми необхідно:

1) зробити деяку кількість вимірів і в отриманій вибірці знайти мінімальне x_min і максимальне x_max значення вимірюваної величини;

2) знайти ширину Δх одного біна, розділивши різницю (x_max-x_min) на кількість бінов, наприклад, на десять:

;

3) отримані десять бінів послідовно відкласти на осі абсцис, відзначаючи початок і кінець кожного біна;

4) підрахувати кількість значень Δn, що попадають у кожний бін, і відкласти ці числа по осі ординат. Сума цих чисел повинна до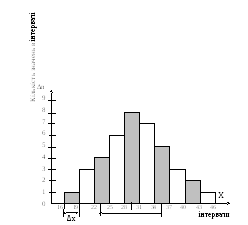рівнювати кількості значень у вибірці (рис. 3).

Рисунок 3 - Гістограма

Побудувавши гістограму, можна зробити висновок про наступні закономірності процесу виміру, що обумовлені впливом випадкових похибок на значення вимірюваної величини:

1) найбільш часто зустрічаються величини, які близькі до середнього значення - вони найбільш імовірні;

2) величини, однаково віддалені від середнього значення, зустрічаються однаково часто - вони рівноймовірні;

3) величини, значно віддалені від середнього значення, малоймовірні.

Якщо збільшувати об'єм вибірки й зменшувати ширину бінів, то ламана лінія в граничному випадку перетворюється в плавну симетричну криву, що має вигляд колоколу.

1.3.2 Нормальний розподіл і його характеристики

Розглядаючи випадкові похибки як один з видів випадкових подій, німецький математик Гаус установив закон розподілу похибок вимірів залежно від своєї величини. Цей закон називається законом нормального розподілу або розподілом Гауса. На рисунку 4 наведена крива, що відповідає цьому закону.

f(x)

-3σ -2σ -σ 0 σ 2σ 3σ

Відхилення від дійсного значення

Рисунок 4 - Графік нормального розподілу

Крива показує:

1) найбільш імовірні випадкові похибки, близькі до нуля;

2) зі збільшенням величини похибки ймовірність їхньої появи швидко зменшується;

3) похибки, рівні по величині, але протилежні за знаком, рівно ймовірні;

4) при вимірюваннях з однаковою точністю найбільш імовірним значенням вимірюваної величини є середнє арифметичне із всіх результатів.

Крива нормального розподілу відповідає теоретичному випадку нескінченно великої кількості вимірювань n, при якому величини похибок невідривно заповнюють всю область значень ±Δх. Аналітичний вираз, що описує криву нормального розподілу (закон Гауса) має вигляд:

,

де σ – дисперсія розподілу величини Δх.

З теорії випливає, що при n>30

,

де - відхилення значення вимірюваної величини від середнього, котре називається випадковою абсолютною помилкою одиничного вимірювання.

Величину називають генеральною середньою квадратичною помилкою.

При досить точних вимірюваннях величина σ мала, а при грубих вимірах спостерігається великий розкид результатів, і значення σ буде більшим. У випадку реального числа вимірювань їхнє число буде кінцевим. У цьому випадку не має сенсу говорити про ймовірність появи похибки даної величини, а говорять про ймовірність появи похибки, що лежить у межах деякого інтервалу ±Δ_х. Інтервал ±Δ_х називається довірчим, а ймовірність Р влучення будь-якого значення вимірюваної величини в довірчий інтервал, називається довірчою ймовірністю або надійністю.

Розрахунки площ, обмежених кривою розподілу, для різних дають наступні результати:

±Δх	≤0,1σ	≤0,5σ	≤σ	≤2σ	≤3σ
Р	0,08	0,38	0,68	0,95	0,98

Для звичайних вимірювань можна обмежитися Р = 0,95. Для вимірювань, у яких необхідна висока надійність, задають Р = 0,98.