Контрольні питання

1. Як класифікуються електровимірювальні прилади, що використовуються для вимірювання електричних величин?

2. Що таке межа вимірювання приладу? Як визначити ціну поділки?

3. Що таке клас точності приладу?

4. Як визначається внутрішній опір амперметра і вольтметра?

5. Як підключають в електричну схему амперметр, вольтметр? Чому?

6. Що таке електричний струм? В яких одиницях вимірюється?

7. Який струм називають постійним?

8. Які умови тривалого існування електричного струму?

9. Що таке напруга? В яких одиницях вимірюється?

10. Що таке опір матеріалу? В яких одиницях вимірюється?

11. Що стверджує закон Ома для однорідної ділянки кола, для замкнутого кола?

12. Що таке ЕРС?

13. Як визначити корисну потужність і потужність джерела? В яких одиницях вимірюється потужність?

14. Як визначити загальний опір послідовно з’єднаних провідників?

15. Як визначити загальний опір паралельно з’єднаних провідників?

Лабораторна робота № 108 Дослідження залежності напруженості магнітного поля в центрі соленоїда від сили струму в його обмотці

Мета роботи - визначити напруженість магнітного поля в центрі соленоїда по періоду коливань магнітної стрілки при різних значеннях сили струму в його обмотці, побудувати графік залежності напруженості від сили струму.

Прилади і обладнання: соленоїд, магнітна стрілка, яка підвішена на непружній нитці, міліамперметр, реостат, двополюсний перемикач, секундомір.

Теорія методу і опис установки

Соленоїд — катушка циліндрової форми з дроту, витки якої намотані в одному напрямі. Його магнітне поле є результатом додавання полів, створених круговими струмами витків обмотки, що розташовані один біля одного і мають загальну вісь. В центральній частині достатньо довгого соленоїда густина силових ліній постійна, тобто поле практично однорідне (рис. 1).

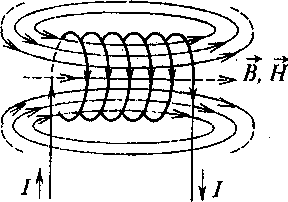
Рисунок 1

Воно виявляється по силовій дії на провідники із струмом або на постійні магніти (магнітні стрілки), які внесені в полі.

Силовими характеристиками магнітного поля є вектор магнітної індукції і вектор напруженості , які зв'язані між собою співвідношенням:

, (1)

де – магнітна стала в системі СІ;

– відносна магнітна проникність середовища ( для соленоїда без сердечника)

Магнітна індукція чисельно дорівнює максимальній силі dF, діючій з боку поля на одиницю довжини dl провідника, по якому тече електричний струм I одиничної сили і який розташований перпендикулярно до напряму магнітного поля

що виходить із закону Ампера

Вектор направлений по дотичній до силової лінії поля – лінії магнітної індукції,яка визначається за правилом правого гвинта: напрям лінії магнітної індукції співпадає з напрямом обертання головки гвинта, якщо його поступальний рух співпадає з напрямом струму в провіднику.

Лінії магнітної індукції завжди замкнуті і охоплюють провідник із струмом (рис.1, 2).

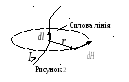
Сили, які діють з боку магнітного поля на північний і південний кінці магнітної стрілки, завжди прагнуть встановити її уздовж силової лінії поля (рис. 3). Тому напрям магнітного поля в даній точці можна визначити як напрям, який вказує північний полюс магнітної стрілки (стрілки компаса), поміщеної в цю точку.

Величина індукції магнітного поля в будь-якому середовищі залежить від його властивостей.

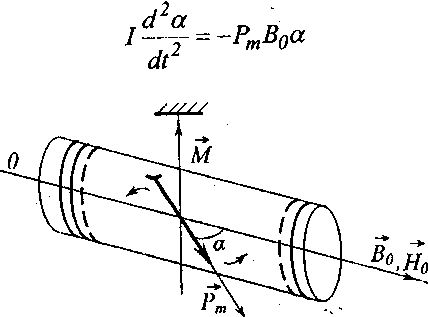
Рисунок 3

Згідно закону повного струму для магнітного поля в вакуумі (теорема про циркуляцію вектора ) циркуляція вектора по довільному замкнутому контуру дорівнює добутку магнітної сталої на алгебраїчну суму струмів, що охоплюється цим контуром

,

де - вектор елемента довжини контура, направлений вздовж обходу контура;

- проекція вектора на дотичну до контура;

- кут між векторами і ;

n – кількість провідників зі струмом, які охоплює контур L довільної форми.

Цей закон можна використати для розрахунку магнітного поля соленоїда. Отже, магнітна індукція поля всередині соленоїда у вакуумі дорівнює:

, (2)

де N - число витків соленоїда;

l – довжина соленоїда, м;

п – число витків на одиницю довжини соленоїда, ;

I – сила струму в його обмотці

Напруженість магнітного поля не залежить від властивостей середовища.

З формул (1) та (2) можна отримати напруженість магнітного поля в центрі довгого соленоїда:

, (3)

Якщо в центрі соленоїда розташувати магнітну стрілку, підвішену на тонкій невагомій і непружній нитці, то при пропусканні струму по обмотці соленоїда магнітне поле останнього приведе стрілку в коливальний рух. Період цих коливань залежатиме від величини і напряму магнітного поля соленоїда, а враховуючи (3) від сили струму в його обмотці. Визначаючи експериментально період коливань стрілки при різних значеннях сили струму, можна досліджувати залежність напруженості магнітного поля в центрі довгого соленоїда від сили струму в його обмотці.

За відсутності струму в соленоїді на магнітну стрілку діє тільки магнітне поле Землі. Тому на даній широті місцевості вона завжди буде орієнтована уздовж одного і того ж напряму - уздовж силової лінії магнітного поля Землі. При відхиленні стрілки на невеликий кут (рис. 3), сила, діюча на стрілку з боку цього поля, прагне повернути її в первинне положення.

Згідно основному закону динаміки обертального руху сумарний момент сил, діючий на стрілку:

, (4)

де – векторна сума моментів сил, діючих на стрілку;

J – момент інерції стрілки;

– її кутове прискорення, причому:

(5)

В рівнянні (4) для магнітної стрілки не будемо враховувати момент сили деформації (кручення) нитки, оскільки вона непружна. Механічний момент сили, діючий з боку магнітного поля Землі:

або в скалярній формі ,

де – магнітний момент стрілки;

– індукція однорідного магнітного поля Землі (горизонтальна складова);

– кут між векторами і .

Для малих кутів відхилення , тому можна прийняти, що

(6)

Рівняння динаміки (4) для стрілки, що відхилюється первинно на кут (рис. 3), з урахуванням (5) і (6), є диференційним рівнянням вільних гармонійних коливань:

(7)

Знак «–» враховує те, що М (6) є повертаючим моментом.

Перепишемо рівняння (7) у вигляді:

і позначимо (8)

Тоді .

Рішення цього рівняння має вигляд: ,

де– кут повороту стрілки у момент часу ;

– амплітудне значення цього кута;

– циклічна частота коливання стрілки;

– початкова фаза коливань.

При пропусканні струму по обмотці соленоїда магнітна стрілка знаходиться під дією двох магнітних полів: поля Землі і поля соленоїда. За принципом суперпозиції магнітних полів результуюче поле в місці розташування стрілки . Оскільки, індукція поля і, отже, дія поля на магнітну стрілку залежатиме від напряму вектора, чисельне значення якого при незмінній густині витків визначається величиною сили струму в обмотці соленоїда (2), а також напрямом струму (см. правило правого гвинта). На циклічній частоті коливань стрілки (8) це позначиться таким чином. Вона може дорівнювати:

а) при збігу магнітних полів соленоїда і Землі:

(9)

б) при протилежному напрямі цих полів:

(10)

Для виключення невідомих і J додамо рівняння (9) і (10). Результат розділимо на (8). Одержимо 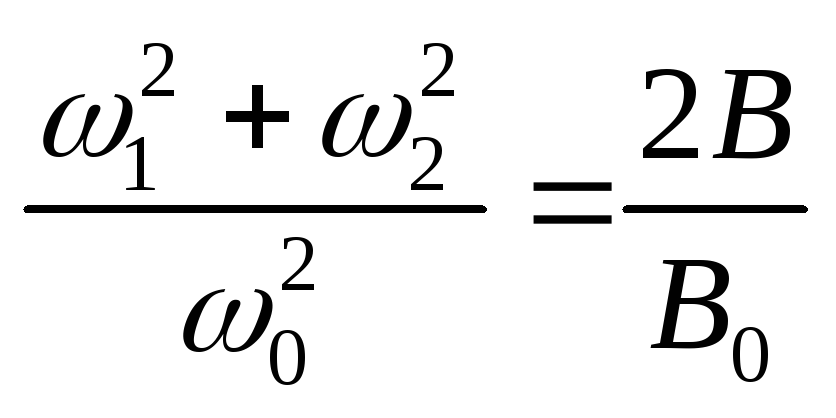. Звідки магнітна індукція В в центрі соленоїда:

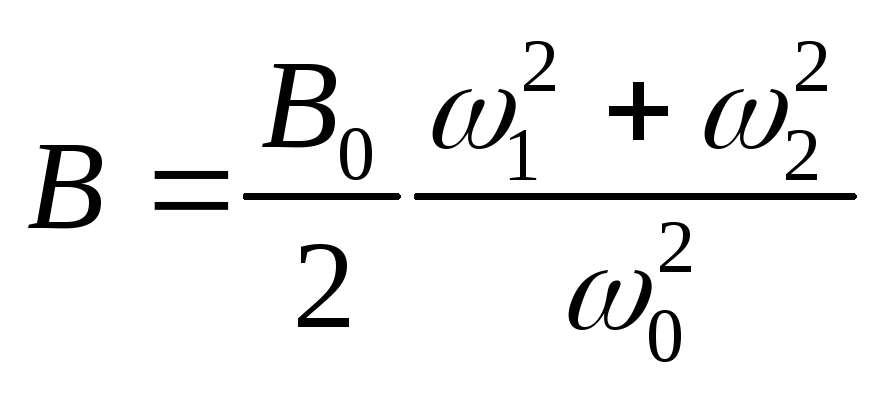(11)

Виразимо циклічні частоти через періоди коливань

, (12)

а індукцію магнітних полів В і В₀ – через відповідні їм напруженості Н, Н₀ (1)

. (13)

Підставивши вирази (12) і (13) в (11), одержимо розрахункову формулу для обчислення напруженості магнітного поля Н в центрі соленоїда

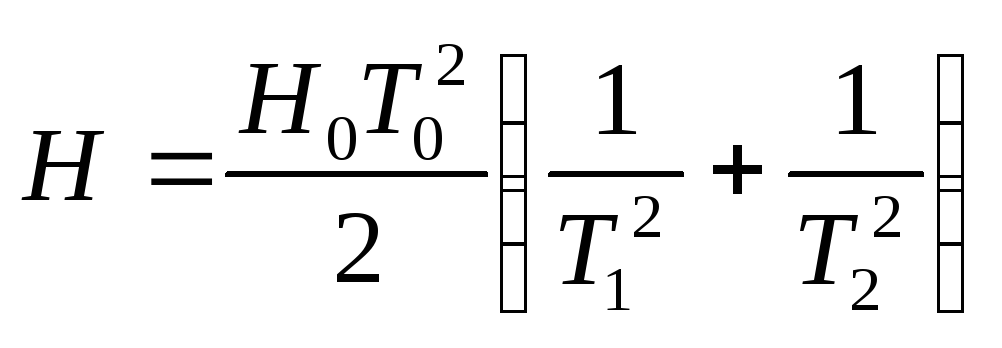, (14)

де – період вільних коливань магнітної стрілки в полі Землі (струм в соленоїді відсутній);

, – періоди коливань магнітної стрілки в результуючому полі Землі і соленоїда для певного значення струму в обмотці, причому, відповідає одному з напрямів струму в обмотці, а – протилежному;

– напруженість магнітного поля Землі для географічної широти м. Алчевська.