Федеральное агентство по образованию Ульяновский государственный университет	Форма
«Криптографические методы защиты информации»

ЛАБОРАТОРНЫЕ РАБОТЫ

по курсу

«Криптографические методы защиты информации»

Лабораторная работа 1.

Тема: симметричные криптосистемы.

Цель работы: Разработать криптографическую защиту информации, содержащейся в текстовом (двоичном) файле данных, с помощью алгоритма шифрования, указанного в варианте. Для этого:

1. Разработать алгоритмы шифрования и расшифрования открытого текста из алфавита A=Z_n на заданном ключе с помощью метода, указанного в варианте.

2. Определить алфавит A криптосистемы (открытого текста и шифртекста). Если алфавит A не задан в варианте, выбрать его самостоятельно, так, чтобы он включал в себя символы используемого в примере открытого текста. Например, русский, английский, ASCII. Поставить символам исходного алфавита A в соответствие символы из алфавита Z_n (n – основание алфавита).

3. Написать функцию генерации случайных ключей шифра, оценить размерность ключевого пространства.

4. Написать функцию, реализующую шифрование на заданном ключе открытого текста, состоящего из символов заданного алфавита. Открытый текст, ключ и шифртекст должны быть представлены отдельными файлами.

5. Написать функцию для реализации алгоритма расшифрования полученного шифрованного файла при известном ключе.

Варианты заданий.

1. Шифр простой замены.

2. Шифр сдвига с числовым ключом. Алфавит A – ASCII..

3. Шифр сдвига с символьным ключом. Алфавит A – латинские буквы и символ пробела.

4. Аффинный шифр.

5. Преобразование биграмм аффинным шифром. (не путать с аффинным блочным шифром)

6. Преобразование триграмм аффинным шифром. (не путать с аффинным блочным шифром)

7. Шифр Виженера с ключевым словом. Алфавит A – латинские буквы и символ пробела.

8. Шифр Виженера с числовым ключом. Алфавит A – ASCII.

9. Многопетлевые подстановки. Алфавит A – латинские буквы и символ пробела.

10. Многопетлевые подстановки. Алфавит A – ASCII.

11. Аффинный блочный шифр для 3-грамм.

12. Аффинный блочный шифр для 4-грамм.

13. Шифр Хилла для 3-грамм.

14. Шифр гаммирования с линейным конгруэнтным генератором ключей. Алфавит A – латинские буквы и символ пробела.

15. Шифр гаммирования с линейным конгруэнтным генератором ключей. Алфавит A – ASCII.

16. Шифр перестановки.

17. Шифр пропорциональной замены (шифр омофонов).

Лабораторная работа 2. Тема: криптоанализ симметричных криптосистем.

Провести эксперимент по определению практической стойкости алгоритма, разработанного в лабораторной работе №1.

Считать, что противнику известен алгоритм шифрования, известен набор открытых текстов и соответствующий набор шифрованных текстов. Выбрать наилучший с его точки зрения алгоритм подбора ключа и обосновать свой выбор. Использовать методы:

- анализа статистических свойств шифртекста (частот появления букв).

- силовую атаку (полный перебор ключей).

- другие (если есть более эффективные)

С помощью программы, реализующей выбранный алгоритм крип­тоана­лиза провести эксперимент по вскрытию шифртекс­тов различного размера.

При использовании статистического криптоанализа исполь­зовать табли­цы, приведенные в приложении 1 или подсчитать частоты появления букв используемого алфавита в тексте, частью которого является текст примера.

Построить графики зависимости времени криптоанализа от параметров ал­горитма шифрования (длины или других параметров ключа, размера шифр­текста или др., в зависимости от алгоритмов шифрования и криптоанализа).

В результате эксперимента определить параметры алгоритма шифрования (размер передаваемого текста, размер и характеристи­ки ключа, объем ключевого пространства и другие параметры алгоритма шифрования), необходимые для практической криптостойкости разработанного в лабораторной работе №1 алгоритма шифрования.

Практической криптостойкостью в данной работе будем считать невозможность взлома шифра противником, имеющим в распоряжении один ПК мощности, равной мощности компьютера, на котором делалась работа и один час времени.

Лабораторная работа 3. Тема: поточные шифры. Шифр Вернама. Моделирование работы разрядного скремблера.

Простейшей и в то же время наиболее надежной из всех схем шифрования является так называемая схема однократного гаммирования, изобретение, которое чаще всего связывают с именем Г.С. Вернама.

Гаммирование – это наложение (снятие) на открытые (зашифрованные) данные криптографической гаммы, то есть последовательности элементов данных, вырабатываемых с помощью некоторого криптографического алгоритма, для получения зашифрованных (открытых) данных.

В данной лабораторной работе алфавитом A, в котором записываются открытые и шифрованные тексты, является поле Z₂, то есть открытые и шифрованные тексты рассматриваются как двоичные последовательности. В этом случае "наложение" гаммы - не что иное, как выполнение операции сложения  по модулю 2 (xor), которая, например, в языке программирования Си обозначается знаком ^.

Стандартные операции над битами: 0  0 = 0, 0  1 = 1, 1  0 = 1, 1  1= 0.

Скремблером называется программная или аппаратная реализация алгоритма, позволяющего шифровать побитно непрерывные потоки информации.

Рассмотрим сдвиговый регистр с обратной связью (Linear Feedback Shift Register, сокращенно LFSR) – логическое устройство, схема которого изобра­жена на рис. 3.1.

Сдвиговый регистр представляет собой последовательность битов. (Количество битов определяется длиной сдвигового регистра. Если длина равна n битам, то регистр называется n-битовым сдвиговым регистром.) Всякий раз, когда нужно извлечь бит, все биты сдвигового регистра сдвигаются вправо на 1 позицию. Новый крайний левый бит является функцией всех остальных битов регистра. На выходе сдвигового регистра оказывается один, обычно младший значащий, бит.

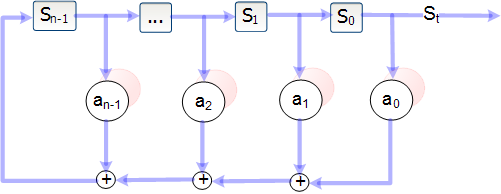
Рис. 3.1. Схема LFSR

При достаточно долгой работе скремблера неизбежно возникает его зацикливание. По выполнении определенного числа тактов в ячейках скремблера создастся комбинация бит, которая в нем уже однажды оказывалась, и с этого момента кодирующая последовательность начнет циклически повторяться с фиксированным периодом. Данная проблема неустранима по своей природе, так как в N разрядах скремблера не может пребывать более 2^N комбинаций бит, и, следовательно, максимум, через, 2^N-1 циклов повтор комбинации обязательно произойдет. Последовательность бит, генерируемая таким скремблером, называется последовательностью наибольшей длины (ПНД).

Чтобы построить N-разрядный скремблер, создающий ПНД, пользуются примитивными многочленами. Примитивный (базовый) многочлен степени по модулю 2 – это неприводимый многочлен, который является делителем , но не является делителем для всех , являющихся делителями . Неприводимый многочлен степени нельзя представить в виде произведения многочленов кроме него самого и единичного.

Найденный примитивный многочлен степени записывается в двоичном виде, затем отбрасывается единица, соответствующая самому младшему разряду.

Приведем пример 7 разрядного скремблера, генерирующего последовательность с периодом равным : . Начальное значение (начальный ключ) возьмем равным . Для этого сдвигового регистра новый бит генерируется с помощью XOR седьмого и третьего битов (см. рис 3.2).

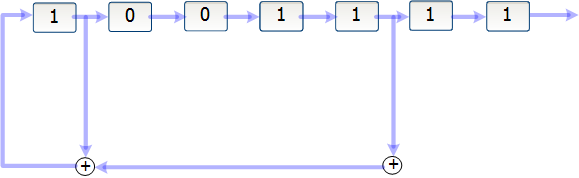
Рис. 3.2. Схема LFSR для многочлена , начальное состояние .