2.7. Уравнение адиабаты идеального газа.
В любой термодинамической системе (простой или сложной) могут протекать три процесса: изотермический (Т = const), адиабатический (Q = 0) и политропный (С = const, где C – теплоемкость). В простой системе, в которой внешним параметром является объем V, а сопряженной ему обобщенной силой – давление Р, возможны еще два процесса: изохорный (V = const) и изобарный (Р = const). Эти пять процессов (изотермический, адиабатический, политропный, изохорный, изобарный) считаются основными в термодинамике, причем адиабатический процесс является частным случаем политропного.
Уравнения изохорного, изобарного, изотермического процессов для идеального газа получаются из уравнения состояния PV = RT:
РV = const – уравнение изотермы;
Р = аТ, где а = R/V = const – уравнение изохоры;
V = a1T, a1 = R/P = const – уравнение изобары.
Получим уравнение адиабатического расширения (сжатия) идеального газа. Примем, что система совершает только работу расширения и процесс является обратимым (равновесным). Тогда
Для идеального газа
,
следовательно
.
Поскольку процесс адиабатический, то δQ = 0 и, с учетом того, что
,
,
получаем
.
Разделим левую и правую часть на (СV·Т):
,
, (2.47)
где
– адиабатический коэффициент ( > 1
для любых систем).
Уравнение (2.47) является дифференциальным уравнением адиабаты в переменных Т и V. Проинтегрировав уравнение (2.47) с учетом того, что теплоемкости СV и Сp (а значит, и адиабатический коэффициент) идеального газа не зависят от температуры и объема, получим:
,
,
(2.48)
Уравнение (2.48) есть уравнение адиабаты идеального газа в переменных Т и V. В переменных P и V уравнение адиабаты принимает вид
, (2.49)
так как
,
.
И, наконец, уравнение адиабаты в переменных Р и Т имеет вид
, (2.50)
поскольку
,
.
Уравнения адиабаты (2.48) – (2.50) называются уравнениями Пуассона.
Теплоемкости одноатомных и двухатомных идеальных газов постоянны и равны:
|
Идеальный газ |
Сp |
CV |
|
|
одноатомный |
|
|
|
|
двухатомный |
|
|
|
Величину γ для реальных газов можно определить, измеряя скорость звука в газе:
,
где М – молярная масса газа.
Далее, зная величину , можно, используя в первом приближении уравнение Майера, рассчитать изохорную и изобарную теплоемкость газообразного вещества:
,
,
,
,
.
При адиабатическом расширении (сжатии) газа Q = 0 и
,
то есть положительная работа совершается за счет убыли внутренней энергии. Следовательно, если идеальный газ адиабатически расширяется (W > 0), то U < 0 и температура газа уменьшается:
только если
.
При адиабатическом сжатии температура газа увеличивается. На практике адиабатическим условиям отвечает быстрое (мгновенное) проведение процессов, когда сравнительно медленно протекающий теплообмен мало влияет на изменение внутренней энергии и температуры. Так, при адиабатическом сжатии газа ударной волной газ не успевает отдать выделившуюся теплоту и сильно нагревается.
Используя уравнения адиабат идеального газа, можно получить несколько уравнений для работы равновесного адиабатического процесса. Так как для адиабатического процесса
и
,
то
.
Поэтому работа расширения одного моля идеального газа равна
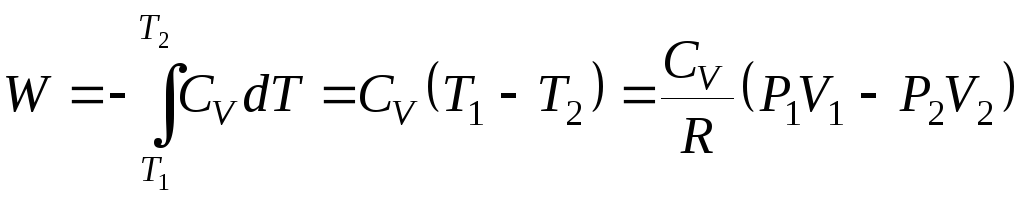, (2.51)
а
так как
и
,
то
. (2.52)
Следует отметить, что для необратимого адиабатического расширения (сжатия) газа уравнения Пуассона неприменимы. Однако по-прежнему справедливо соотношение
,
а работа необратимого расширения газа против постоянного внешнего давления равна
.