1.4.2. Консольная балка

При колебаниях балки момент изгиба в сечении X равен

, (19)

а уравнение её упругой линии

. (20)

Интегрируя дважды выражение

,

получим

. (21)

При x=L имеем

. (22)

Тогда формулу (21) можно представить в виде

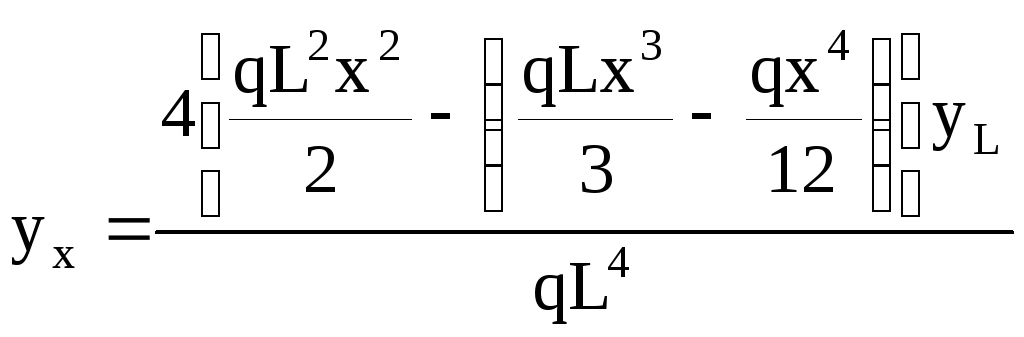. (23)

Кинетическая энергия элемента dx равна

, (24)

а всей балки

.

Из условия получаем

, (25)

а для любого сечения балки при

. (26)

1.4.3. Двухопорная балка постоянного сечения

Аналогично п. 1.4.2 получаем

, (27)

, (28)

. (29)

Прогиб по середине балки

. (30)

Из условия

(31)

после интегрирования и преобразований получаем

, (32)

а для любого сечения x балки

. (33)

В табл. 1 приведены формулы для определения приведённых масс.

1.5. Определение жесткости элементов, механизмов и машин

Под жесткостью механической системы или отдельного её элемента понимают отношение нагрузки к вызываемой ею деформации.

В общем, виде линейная жесткость равна

, , (34)

а угловая жесткость

, , (35)

где P – растягивающее, сжимающее или изгибающее усилие;

Таблица 1

Формулы для определения приведенных масс

	При x=L

y – перемещение в сечении, в котором прикладывается деформирующее усилие;

M – крутящий момент;

– угол закручивания в сечении, в котором прикладывается крутящий момент.

Для конкретных элементов (стержни, валы переменного сечения, балки, пружины, рессоры и т.п.) методами теории упругости находят деформацию элемента (y или ) в рассматриваемом сечении и определяют его жесткость.

Жесткость элемента зависит от следующих факторов:

• материал (Е, G);

• форма поперечного сечения (за исключением растяжения и сжатия);

• место (координата) приложения нагрузки;

• способ закрепления концов.

Иногда в расчетах удобнее пользоваться понятием податливость

, . (36)

Для определения жесткости элементов сложной формы (лопасти, вилки, зубья шестерен и т.п.) часто используют эмпирические формулы, включающие различные коэффициенты, учитывающие соотношения размеров элементов.

В табл. 2 приведены формулы для определения жесткости элементов, наиболее часто встречающихся в машинах и механизмах металлургических машин.

1.6. Приведение жесткостей системы

Жесткости звеньев, соединяющих приведенные массы, также должны быть приведенными.

Рассмотрим систему, состоящую из поступательно движущихся масс (рис. 12а), нагруженных силами , , , , …, .

Если приведение системы производят к массе m_П, приведенная жесткость расчетной системы определяется следующим образом.

Статическая сила P₁, действующая на массу m₁, вызовет перемещение за счет упругой деформации звена c₁; перемещение массы m₂, соответственно, равно , перемещение следующей массы m₃ составит и т.д., т.е. перемещение массы m₁ под действием силы P₁

(37)

Таблица 2

Формулы для определения жесткости элементов систем*

Схема элемента	Описание элемента	Жесткость, податливость
1	2	3
	Стержень постоянного сечения (S=const)
	Плоский стержень трапецеидального профиля (S=var)
	Ступенчатый стержень	При x=L
	Консольная балка при I=const
	Консольная балка при Ix=var, I – в сечении заделки
	Консольная балка при Ix=var, I – в сечении заделки	При

* S и I – площадь и момент инерции поперечного сечения соответственно.